[JAVA] 자바는 어떤 정렬 알고리즘을 사용할까?

들어가며

자바에는 Arrays와 Collections에서 static 메서드로 정렬 기능을 제공한다. 정렬 알고리즘을 썼을 테니 시간복잡도가 O(NlogN)이겠거니 생각해왔다. 생각해보면 정렬 알고리즘에도 여러 종류가 있는데, 어떤 장단점이 존재해서 특정 알고리즘을 선택해서 구현하였는지 궁금했다. 정렬 알고리즘들의 원리, 장단점과 실제 자바에서 어떻게 사용하고 있는지가 이번 게시글의 주제이다.

Arrays.sort()와 Collections.sort()가 사용하는 정렬 알고리즘

Arrays.sort()

1. Array of Primitives
   DualPivotQuicksort.sort() 를 사용한다. 클래스명만 보면 Quick sort만 사용할 것 같지만, 다양한 알고리즘으로 최적화되어 있다. (^^)

There are also additional algorithms, invoked from the Dual-Pivot Quicksort, such as mixed insertion sort, merging of runs and heap sort, counting sort and parallel merge sort.

여기에서 dual-pivot이라는 것은 말 그대로 pivot이 2개인 Quick sort를 사용한다. 전형적인 one-pivot Quick sort보다 (시간복잡도는 같지만) 성능이 좋다.

2. Array of Objects
   ComparableTimSort.sort() 를 사용한다. 즉, Tim sort를 사용한다. Tim sort는 Merge sort와 Insertion sort를 결합한 알고리즘이다.

왜 Primitives와 Objects를 기준으로 다른가?

안정성 때문이다. Quick sort는 불안정(unstable) 정렬이고 Merge sort는 안정(stable) 정렬이다. 같은 정렬 기준이 충족되는 값에 대해 초기 순서가 유지되면 stable하고, 유지되지 않는다면 unstable하다.

자바 API docs의 Arrays 부분을 보면 아래와 같이 적혀 있다.

Such descriptions should be regarded as implementation notes, rather than parts of the specification. Implementors should feel free to substitute other algorithms, so long as the specification itself is adhered to. (For example, the algorithm used by sort(Object[]) does not have to be a MergeSort, but it does have to be stable.)

Merge sort를 다른 알고리즘으로 대체할 수 있겠지만 sort(Object[])는 반드시 stable해야 한다. Primitives야 값 자체를 저장하지만 참조 타입의 경우 메모리 주소에 따라 다른 대상이기 때문에 정렬 전, 후에서 '같은 정렬 기준이 충족되는 값'들이 같은 순서를 가지는게 유용하다. 예를 들어, Person이라는 객체에 age와 name 필드가 있을 때 먼저 age로 정렬하고 name으로 정렬한다면 같은 name의 Person들은 age로 정렬될 것이다.

Collections.sort()

List 인터페이스의 default 메서드인 sort를 호출한다. 그리고 이 메서드에서는 Arrays.sort()를 호출한다. 아래 코드를 보면 Object 배열을 정렬하는 것과 동일하다.

// List의 sort 메서드
Object[] a = this.toArray();
Arrays.sort(a, (Comparator) c);

시간복잡도와 지역 참조성

시간 복잡도가 O(NlogN)인 두 알고리즘이 있다 하더라도 실험적으로 실행 시간을 봤을 때 더 빠른 알고리즘이 있을 수 있다. 예를 들어, Heap sort와 quick sort를 보면 Heap sort가 최악의 경우조차 시간 복잡도가 O(NlogN)이라 전반적으로 더 우수할 것 같지만, 평균을 보면 quick sort가 더 우수하다. 이는 참조 지역성(Locality of Reference) 때문이다.

알고리즘의 실제 실행 시간은 C * 시간복잡도 + ɑ 다. ɑ 부분보다 큰 영향을 주는 C 부분은 참조 지역성으로 좌우된다. Heap sort는 비교하는 인덱스가 현재 인덱스의 2배이기 때문에 참조 지역성이 좋지 않다. 따라서 평균에서 같은 O(NlogN)이더라도 quick sort가 더 빠른 것이다.

DualPivotQuicksort

다양한 알고리즘을 heuristic하게 사용한다.
제가 코드를 보고 이해하며 적은 것이기 때문에 부족하거나 부정확한 부분이 있다면 댓글로 알려주시면 감사하겠습니다. (최대한 구글링으로 알고 있는 것이 맞나 확인하며 적었습니다.)

Quick sort가 기반이다

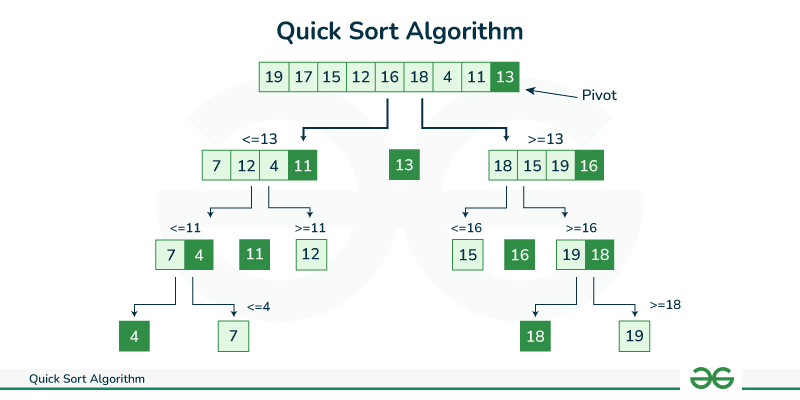위 사진은 가장 기본적인 구현이다.

시간 복잡도를 봤을 때 최악의 경우(오름차순을 정렬할 때 pivot이 가장 큰 값인 경우) O(N^2)이지만 참조 지역성이 우수하기 때문에 Merge sort나 Heap sort에 비해 평균에서 가장 빠르다. Java API docs에 따르면 100퍼센트는 아니지만 거의 모든 케이스에 대해 DualPivotQuicksort.sort()는 O(NlogN)이라고 한다. 아래 알고리즘들로 최적화한 결과이다.

최선	평균	최악	메모리	안정성
O(NlogN)	O(NlogN)	O(N^2)	O(logN)	X

작은 크기의 배열은 Insertion sort를 사용한다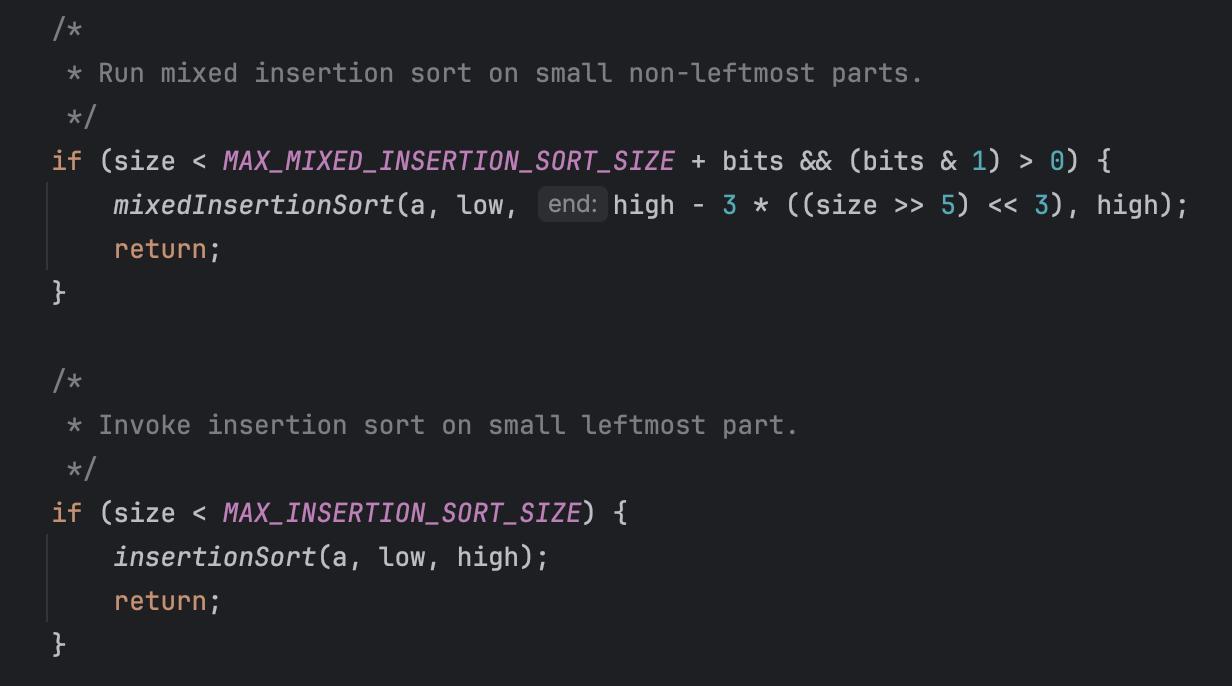

Insertion sort의 시간 복잡도를 보자.

최선	평균	최악	메모리	안정성
O(N)	O(N^2)	O(N^2)	O(1)	O

안좋다. 하지만 Insertion sort는 인접한 배열을 보기 때문에 참조 지역성을 잘 만족하고 C 값이 작아 작은 크기의 배열을 정렬하기에 좋다.

거의 정렬된 상태에서는 Merge sort를 사용한다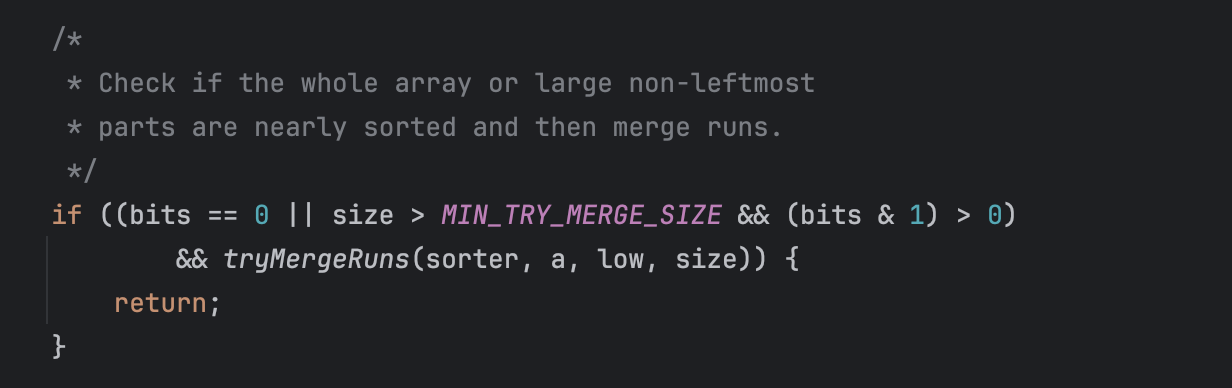

Merge sort는 배열의 일부나 전체가 거의 정렬되어 있는 경우 효과가 더욱 좋다. 병합 과정에서 두 부분 배열을 비교하고 병합하는데 드는 비용이 낮아지기 때문이다. 따라서 배열이 특정 크기 이상이라면 tryMergeRuns를 통해 정렬 상태를 확인하고 Merge sort를 진행한다.

재귀가 깊어질 경우 Heap sort를 사용한다

재귀적 호출이 너무 많아서 실행 시간이 이차 함수(Quadratic)로 증가하는 경우 실행 시간이 비효율적으로 증가하는 것을 방지하기 위해 시간 복잡도가 좋은 Heap sort를 사용한다.

최선	평균	최악	메모리	안정성
O(NlogN)	O(NlogN)	O(NlogN)	O(1)	O

byte 배열은 Counting sort와 Insertion sort를 사용한다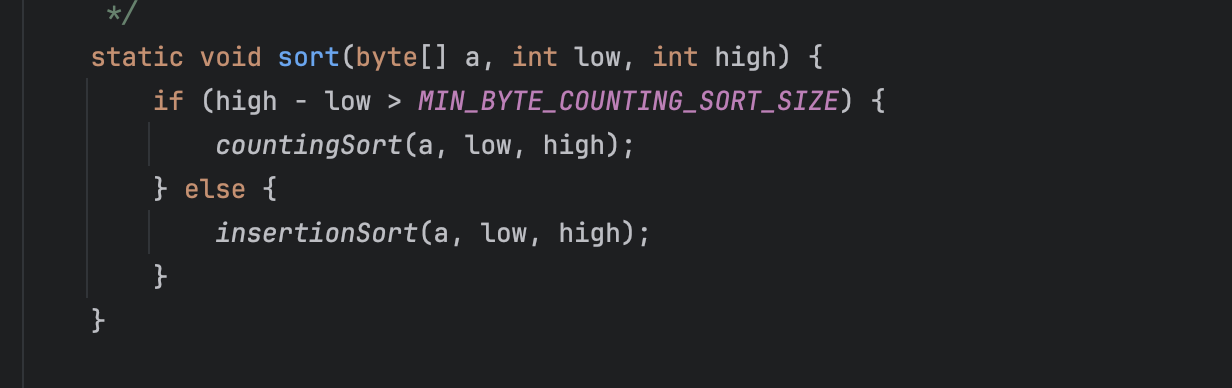

byte type은 8비트만 사용하여 -127에서 +128까지의 정수 값을 표현할 수 있다. 크기가 작기 때문에 Insertion sort를 사용한다. 이 때, 특정 크기 이상이면 Counting sort를 사용한다. 아래 표에서 K는 배열의 최댓값을 의미한다.

최선	평균	최악	메모리	안정성
O(N+K)	O(N+K)	O(N+K)	O(K)	O

배열이 작은데 배열의 요소가 {1, 3, 1000}이라면 1000짜리 배열을 만들고 그만큼 실행 시간도 증가하기 때문에 일정 크기 이상일 때 사용한다.

char 배열과 short 배열도 Counting sort를 일부 사용한다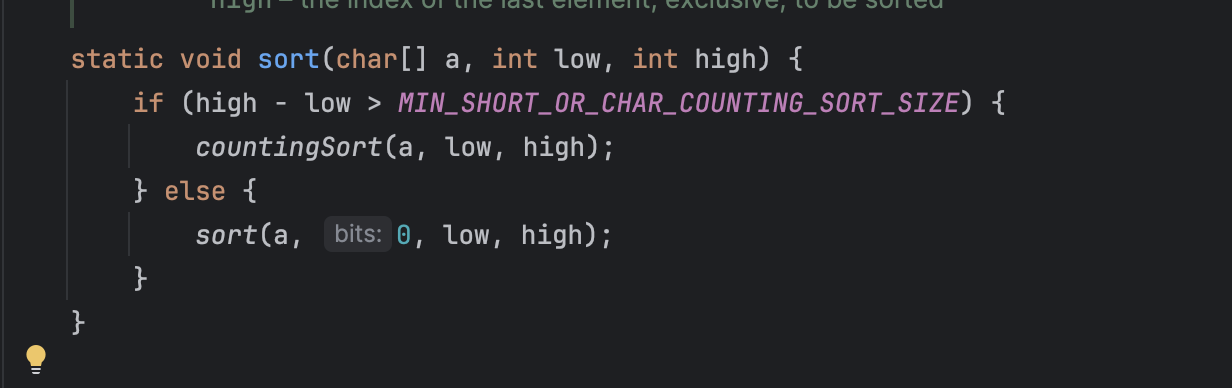

역시 일정 크기 이상이라면 Counting sort를 사용하고 나머지는 dual-pivot Quick sort를 기본으로 사용하는 sort 메서드를 호출한다.

ComparableTimSort

Tim sort만을 사용하기 때문에 이를 이해하면 코드를 보기 쉽다. 다시 언급하자면 Tim sort는 Merge sort + Insertion sort 이다!

Merge sort

시간 복잡도는 좋지만, 입력된 배열만큼 메모리를 추가로 써야한다. 따라서 Tim sort에서는 메모리를 최적화하기 위해 병합할 때 몇 가지 방법을 도입하였다. 자세한 건 Tim sort에 대해 알아보자를 참고하자!

최선	평균	최악	메모리	안정성
O(NlogN)	O(NlogN)	O(NlogN)	O(N)	O

Insertion sort

Insertion sort는 앞서 언급했듯 작은 크기의 배열을 정렬할 때 좋기 때문에 Merge sort를 할 때 나눈 작은 그룹들을 Insertion sort로 정렬한다.

Binary Insertion sort

Tim sort에서 사용하는 Insertion sort는 Binary Insertion sort이다. 자바도 역시 이렇게 구현되어 있다.
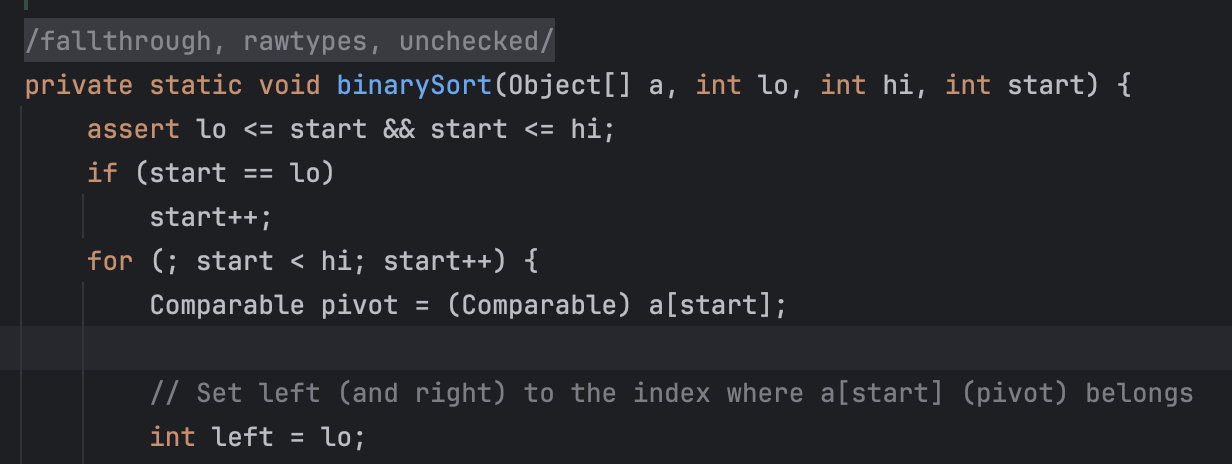원소를 삽입해야 할 위치를 찾을 때 이분 탐색을 활용한다. 참조 지역성은 떨어지지만 O(logN)의 비교로 최적화한다. 원소를 삽입하는 과정은 기존과 동일하게 O(N)이므로 시간 복잡도는 역시 O(N^2)이지만 원소를 삽입하는(나머지 원소들을 시프트하는) 과정은 상대적으로 빠르다.

아래는 binarySort에서 원소를 삽입하는 부분인데, System.arraycopy()로 빠르게 나머지 원소들을 복사한다. 배열의 요소를 하나하나 접근해서 복사하는 것이 아니라 지정된 범위의 값들을 한 번에 통째로 복사한다.

            switch (n) {
                case 2:  a[left + 2] = a[left + 1];
                case 1:  a[left + 1] = a[left];
                         break;
                default: System.arraycopy(a, left, a, left + 1, n);
            }

출처

[1]

자바 소스 코드

[2]

https://docs.oracle.com/en/java/javase/17/docs/api/java.base/java/util/Arrays.html

[3]

Tim sort에 대해 알아보자

[4]

자바의 정석

소감

정확하게 알고리즘을 구현하는 것도 물론 중요하겠지만, 적재적소에 활용하는 능력을 키우려면 다른 좋은 예시들을 많이 보고 공부해야 한다고 생각한다. Java API라는 공식적인 레퍼런스가 더할 나위 없이 좋은 예시가 되어 주었다. 최근 Java 자체를 열심히 공부하며 전공 공부했던 기억도 나고 기존 지식들과 연결될 때 보람이 큰 것 같다.