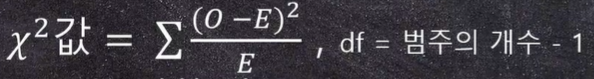
1. 카이제곱?
t-test anova 같은 경우 연속형 종속변수, 명목척도(범주형) 독립변수
만약 둘다 명목 척도라면? t-test,m ANOVA 못씀
이때 사용하는 것이 교차분석
언제 카이제곱 검정을 할까?
변수가 명목척도 일 때,
자료의 값은 개수여야함.
카이제곱 검정의 목적
앞의 t-test나 ANOVA의 경우 둘/셋 이상의 집단의 같은지 다른지
카이제곱 검정의 목적은
변수가 한개인 경우 : 변수 내 그룹 간의 비율이 같은지 다른지
그룹이 단 2개인 경우에는 Binomial test
그룹이 여러개인 경우 카이제곱 검정
변수가 두개 인 경우 : 변수 사이의 연관성이 있는지 없는지
휴대폰 사용과 뇌암
인종과 특정 질병
카이제곱 값

예시
관찰빈도 : 총 고객데이터
기대 빈도 : 총 1,000명의 고객데이터가 있다면 남성/여성 고객 빈도는 500 / 500
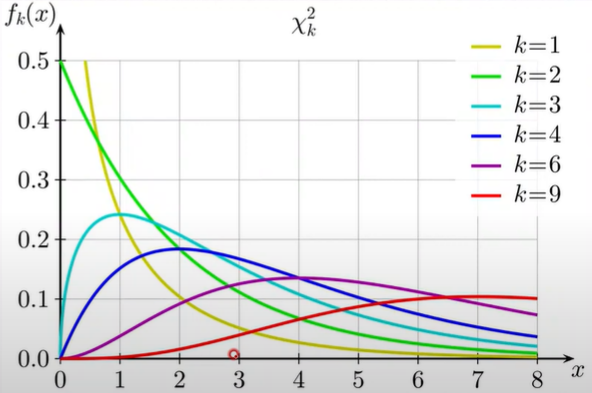
2. 일원 카이제곱 One-way chi-square
변수가 1개라는 의미. 변수가 한개이기 때문에 칼럼 한개로 넣어야함.
당연히 명목척도
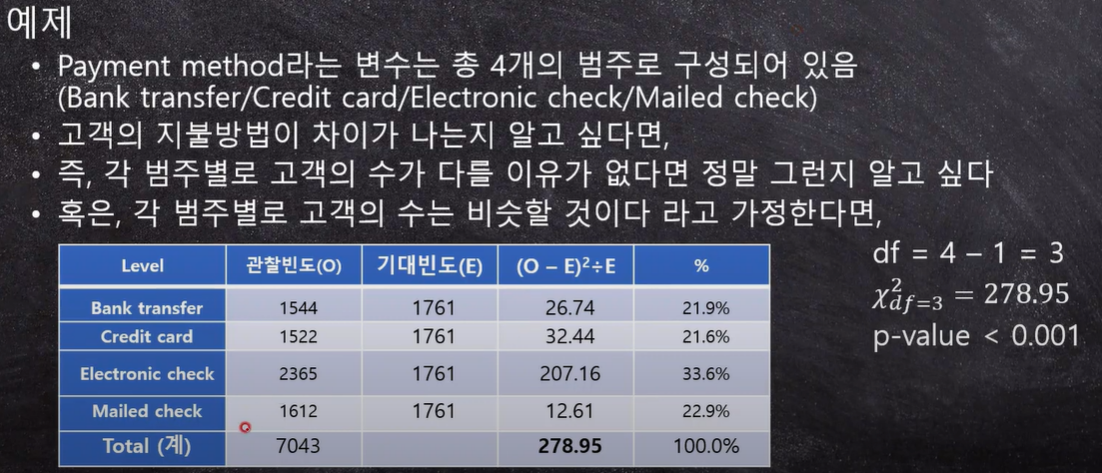
카이스퀘어 값이 278 확실이 큼.
=확실히 유의하다 = 확실히 누군가는 다름
결론적으로
일월 카이제곱 검정의 유의성이 의미하는 것은 무엇인가 다르다 정도임
여기서 다르다는 것 또한 사전에 정해진 기대빈도와 다르다라는 의미
만약 기존의 연구/이론에 의해서 각 범주의 빈도가 다르게 나온다면
기대 빈도 자체를 바꿔서 테스트해야함.
그래서 카이제곱 검정을 적합도 검정이라고 부르기도 함.(Goodness of fit)
3. 이원 카이제곱 Two-way chi-square
변수가 2개라는 의미. 변수가 두개이기 때문에 칼럼도 두개로 나옴.
당연히 명목척도
가장 단순한 형태는 2X2 분석
이때 사용하는 것이 분할 표. = 데이터의 빈도만 단순화 표 작성
예제)
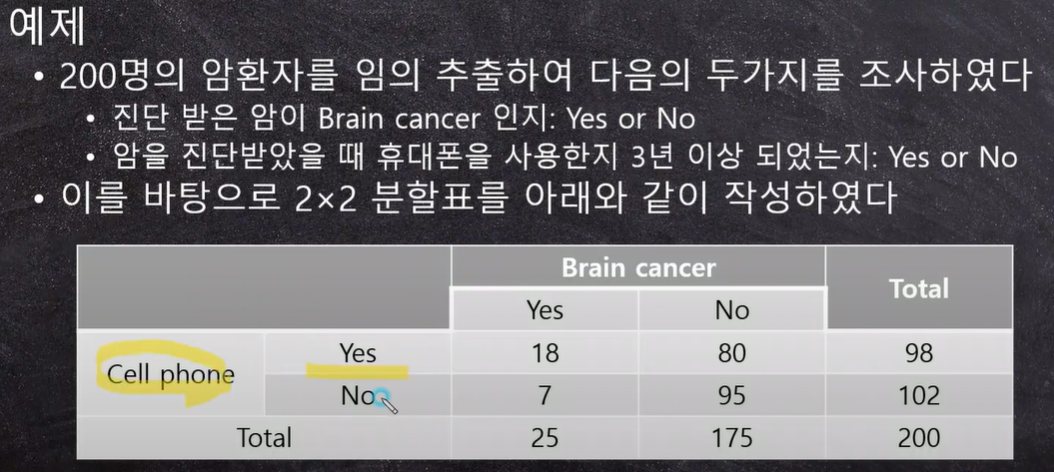
카이제곱 결과는 인과관계를 나타내지 않음. 연관성이 있다!
통계적 연관성을 찾을 수 있으나, 범주 간의 확률의 차이가 얼마나 큰지 알 수 없음
이러한 문제를 해결하기 위해 CI(confidence interval) 을 사용.
4. 카이제곱 심화
한계점
- 랜덤 샘플링
- 독립성
- 각 범주가 서로 배타적이어야 함
- 한 대상이 하나 이상의 범주에 들어갈 수 없음
- 각 셀의 기대빈도가 5 이상이어야 함.(셀 전체의 20%가 5보다 작으면 피셔)
- 경우에 따라 범주를 합쳐야함
- 범주를 합칠 수 없다면, 피셔의 정확검정 or likelihood ratio test(G-test)를 해야함
- df가 1이라면?
- 일원 카이제곱 검정의 경우 범주가 2개 이거나, 이원 카이제곱 검정에서 2x2 인 경우, 비연속성의 조건부 확률을 연속성의 카이제곱분포에 적용함으로써 문제 발생
- 연속성 보정을 하는 Yate's correction 또는 x2 continuity correction을 사용해야함
- 만약 이원 카이제곱 검정의 2x2인 경우 x2 test 결과와 Yate's correction이 다를 경우 피셔의 정확검정을 사용해야함
- 상대 위험도 only 2x2 case
- 상대 위험도(relative risk) = 두 확률의 차이인 P1-P2 가 아니라 P1/P2
- 만약 상대 위험도가 1이라면 두사건이 발생활 확률은 동일
- 1보다 크다면 위험이 증가
- 1보다 작으면 위험이 감소
- 교차비/오즈비(odds ratio)
- 오즈란? Odds = p/1-p
- 확률이 1/2 인 경우 Odds는 1(같음)
- 확률이 3/4 인 경우 Odds는 3(3배 높다)
- 오즈비란? 두 오즈의 비율
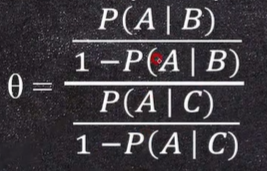
결론 : 핸드폰 비사용자에 비해 3배 높다.- 행렬을 바꿔도 오즈비는 거의 비슷하다.
- 그러나 단순 오즈나 상대 위험도는 변한다.
- 두 명목척도인 변수가 연관성이 있을 경우
- 얼마나 상관관계가 높은지 궁금할 때 상관계수를 구하는 방법
- Phi and Cremer's B
- 분할계수
- 만약 변수가 순위척도인 경우 연관성이 있다면
- 역시 얼마나 상관관계까 높은지 알고 싶다면
kendalls tau-b
Gamma
- 역시 얼마나 상관관계까 높은지 알고 싶다면
5. 카이제곱 검정 실습
한국에서는 인구 통계변수와 내가 가진 변수를 논리없이 묶어서 실습하는 경향이 있음
R로 실행해보려했으나 오류로 나중에 해보기로함
