이분 탐색 (Binary Search)

이분 탐색은 데이터 집합에서 원하는 값을 효율적으로 찾는 알고리즘이다.

정렬된 배열이나 리스트에서 사용되며, 원하는 값과 현재 검사 중인 값의 중간값을 비교하여 데이터를 반으로 나누어 탐색한다.

이분 탐색의 시간 복잡도는 O(log n) 으로 매우 효율적인 검색 알고리즘이다. 대용량 데이터 집합에서도 빠르게 동작한다.

특징

1. 정렬된 데이터 요구

이분 탐색은 데이터가 미리 정렬되어 있어야 한다. 정렬되지 않은 데이터에서는 이분 탐색을 사용할 수 없다.

2. 효율적인 검색

데이터를 절반으로 나누어 찾는 특성 때문에 선형 검색에 비해 효율적이다.

데이터의 크기에 비례하여 검색 시간이 증가하지 않는다.

동작 방식

1. 시작과 끝 인덱스 초기화

처음에는 시작 인덱스와 끝 인덱스를 설정한다.

시작 인덱스는 0 끝 인덱스는 배열 또는 리스트 길이의 -1

2. 중간 값 계산

현재 검색 범위에서 중간 인덱스를 계산하고, 해당 위치의 데이터를 가져온다.

3. 중간 값과 대상 값 비교

중간 값과 대상 값(찾고자 하는 값) 을 비교한다.

• 중간 값과 대상 값이 동일하면 원하는 데이터를 찾았으므로 검색 종료
• 중간 값이 대상 값보다 작으면, 중간 값 이전의 데이터는 필요 없으므로 시작 인덱스 를 중간 값 +1 위치로 설정한다.
• 중간 값이 대상 값보다 크면, 중간 값 이후의 데이터는 필요 없으므로 끝 인덱스 를 중간 값 -1 위치로 설정한다.

4. 검색 범위 조정 및 반복

시작 인덱스 또는 끝 인덱스 설정을 반복하며 중간 값과 대상 값이 일치하거나 검색 범위가 더 이상 없을 때까지 반복한다.

5. 검색 완료

검색 범위가 더 이상 없거나 대상 값을 찾으면 검색이 완료된다.

예시

public class BinarySearchExample {

    public static void main(String[] args) {
        int[] sortedArray = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20};
        int target = 12;

        int result = binarySearch(sortedArray, target);

        if (result != -1) {
            System.out.println("원하는 값 " + target + "을(를) 인덱스 " + result + "에서 찾았습니다.");
        } else {
            System.out.println("원하는 값 " + target + "을(를) 찾지 못했습니다.");
        }
    }
    
    public static int binarySearch(int[] sortedArray, int target) {
        int left = 0;
        int right = sortedArray.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2; // 중간 인덱스 계산

            if (sortedArray[mid] == target) {
                return mid; // 원하는 값 찾음
            } else if (sortedArray[mid] < target) {
                left = mid + 1; // 중간 값보다 크므로 오른쪽 범위로 이동
            } else {
                right = mid - 1; // 중간 값보다 작으므로 왼쪽 범위로 이동
            }
        }

        return -1; // 원하는 값이 배열에 없는 경우
    }


}

---

Lower Bound, Upper Bound

기본적으로 이분 탐색은 정렬된 데이터에서 특정 값이 존재하는지 검색하는 알고리즘이다. 하지만 중복된 데이터에서 탐색할 때는 조금 더 응용된 방법을 사용해야 한다.

예를 들어 중복된 데이터에서 특정 데이터가 몇 개 존재하는지 등 이러한 경우에는 lower bound 와 upper bound를 구해야한다.

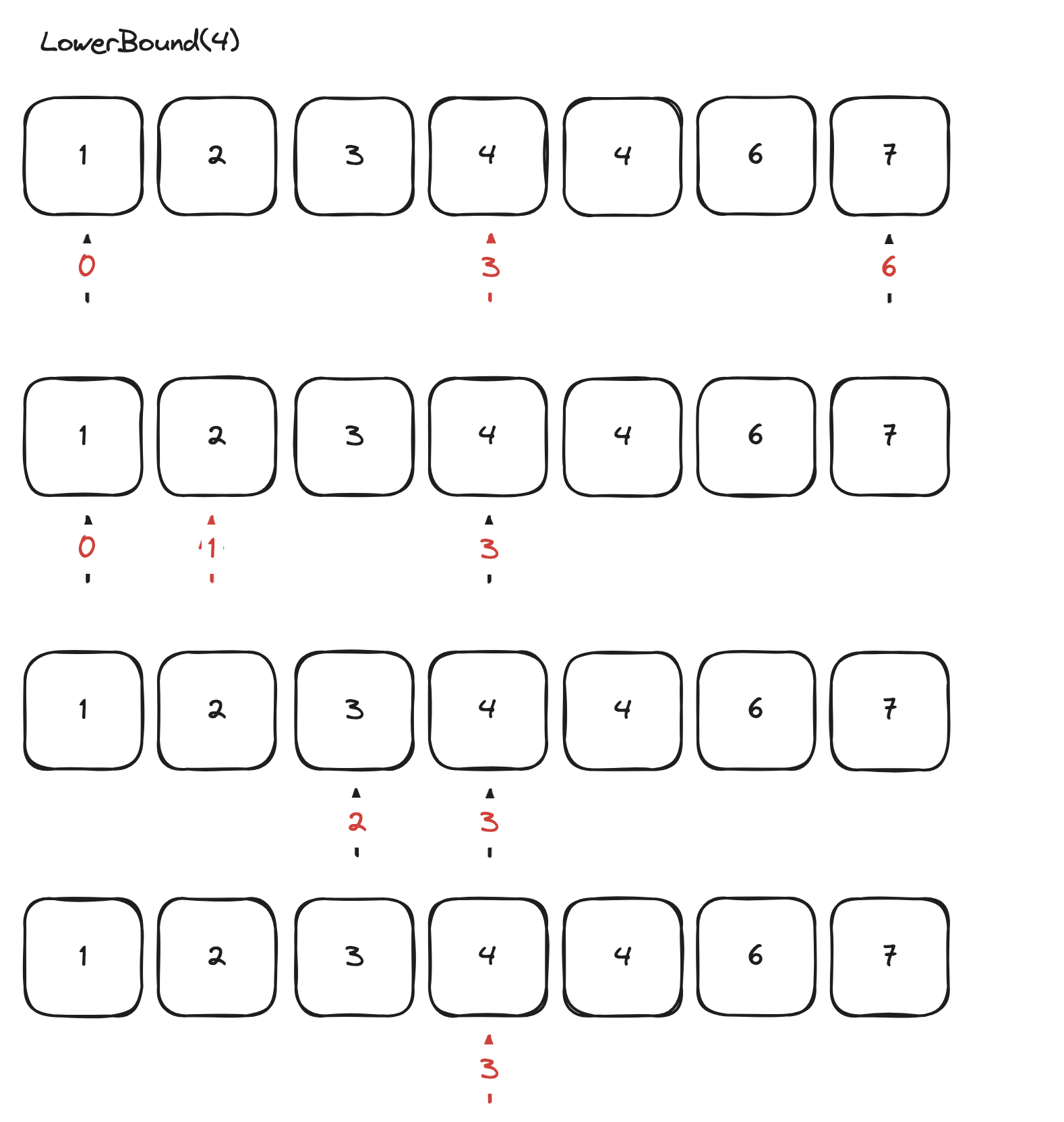
Lower Bound : 데이터 내에서 특정 값보다 같거나 큰 값이 처음 나오는 위치를 리턴해준다.
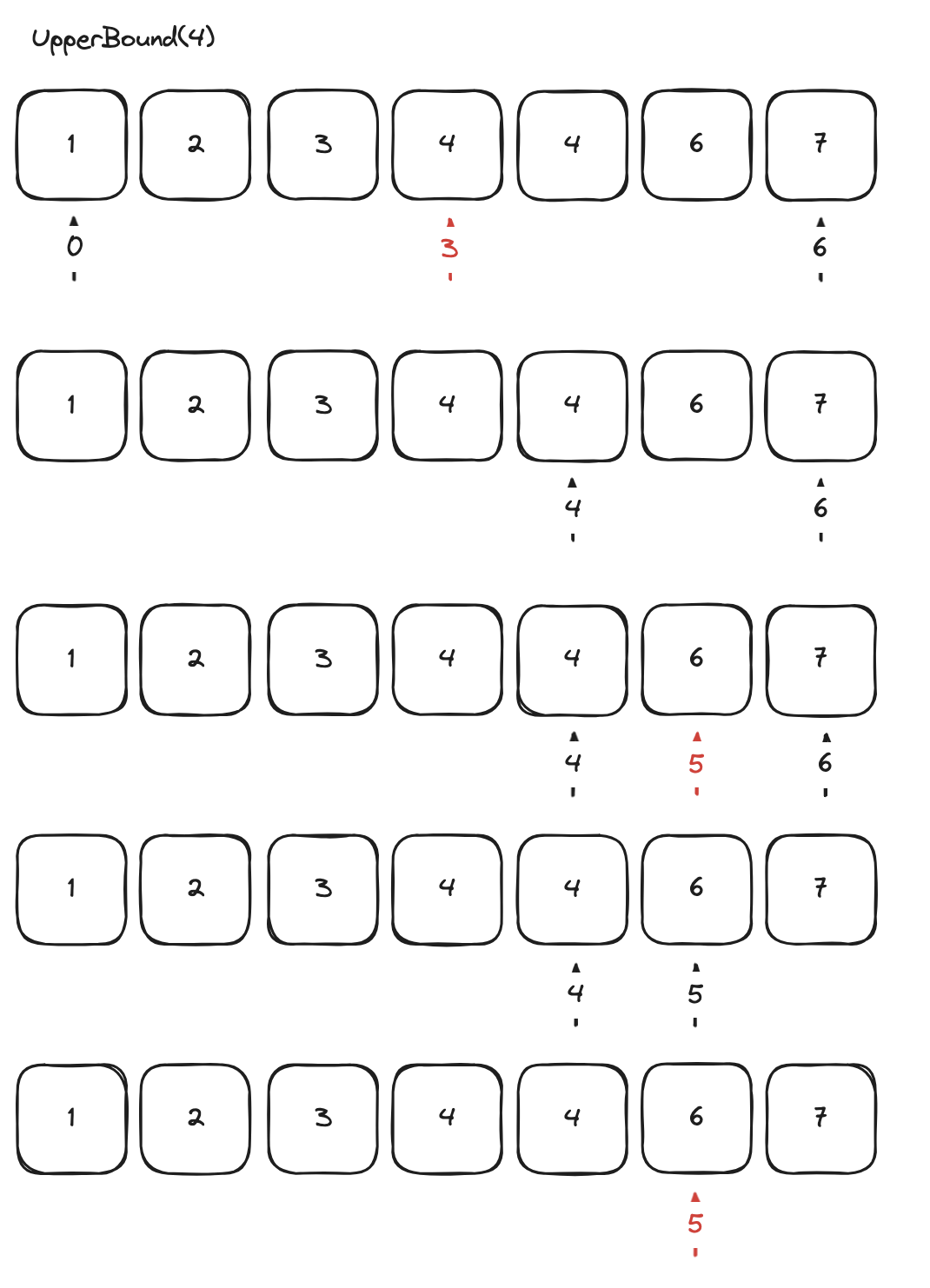
Upper Bound : 특정 값보다 처음으로 큰 값이 나오는 위치를 리턴해준다.

Lower Bound

기본 이진 탐색과 다른 점은 값을 찾았을 때 바로 리턴하는 것이 아니라 처음으로 나오는 값을 찾기 위해 범위를 좁혀가면서 찾는다. end = mid 로 범위를 좁혀간다.

public static int lowerBound(int arr[], int value) {
	int start = 0;
	int end = arr.length;
	int mid = 0;
	while (start < end) {
		mid = (start + end) / 2;
		if (value <= arr[mid]) {
			end = mid;
		} else {
			start = mid + 1;
		}
	}
	return start;
}

Upper Bound

lower bound와 거의 동일하다. 단지 최초로 큰 값이 나오는 곳을 찾기 위해 범위를 좁혀간다.

public static int lowerBound(int arr[], int value) {
	int start = 0;
	int end = arr.length;
	int mid = 0;
	while (start < end) {
		mid = (start + end) / 2;
		if (value < arr[mid]) {
			end = mid;
		} else {
			start = mid + 1;
		}
	}
	return start;
}