조합 (Combination)

조합 알고리즘은 주어진 n개의 값 중 r개의 값을 순서를 고려하지 않고 나열한 경우의 수이다.
순열과 유사하지만 순열은 순서를 고려한다.

조합은 주어진 집합에서 원하는 개수로 만들 수 있는 모든 부분 집합을 생성하는 알고리즘이다.

순서는 중요하지 않고, 중복을 허용하지 않는 경우에 사용된다.

예를 들어 집합 {1, 2, 3} 중 2개의 원소를 선택한 조합을 구하면 {12, 23, 31} 총 3가지 경우의 수가 나온다.

위 예시에서 2가지의 숫자를 박스에 하나씩 넣는 상황을 가정해보자.

1. 3개의 숫자 중 2개의 숫자를 선택하여 나열하는 순열을 구한다.
2. 2개의 공간에 나열된 숫자들은 순서를 부여 받은 상태이므로 그 순서를 부여 받은 상태를 제거해준다면 조합의 경우의 수를 구할 수 있다.

즉, 2개중 2개를 선택하는 순열의 경우의 수로 나누어주면 된다.

n개의 수 중 r개를 선택하는 조합은 nPr의 순열을 구하고, rPr의 순열로 나눈 값을 경우의 수로 가진다.

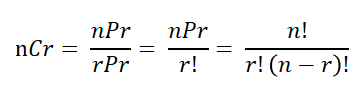
위 그림을 풀면 아래와 같다.

조합 알고리즘은 주로 다음과 같은 상황에서 활용된다.

• 원소의 조합을 찾는 경우 (로또 번호 선택, 카드 게임의 조합)
• 원소들 중에서 특정 조건을 만족하는 조합을 찾는 경우 (특정 합계를 가지는 부분 집합 찾기)

public class Main {  
    // 선택하고자 하는 대상 집합.  
    static int[] target = new int[] { 1, 2, 3 };  
    // 대상 숫자를 담아둘 배열.  
    static int[] result = new int[2];  
  
    public static void main(String[] args) {  
        combination(0, 0);  
    }  
  
    // 조합 메서드(cnt는 선택 횟수, idx는 다음 대상을 선택할때 집합에서 탐색을 시작할 인덱스)
    private static void combination(int cnt, int idx) {  
        // 2개를 선택했으므로, 결과를 출력하고 재귀를 종료
        if (cnt == 2) {  
            System.out.println(Arrays.toString(result));  
            return;
        }  
        // 대상 집합을 주어진 인덱스부터 순회하며 숫자를 하나 선택
        for (int i = idx; i < 3; i++) {  
            // 숫자를 담는다.
            result[cnt] = target[i];  
            // 자신을 재귀 호출(자신 이전의 수를 중복 선택하지 않도록 인덱스를 +1하여 재귀 호출)  
            combination(cnt + 1, i + 1);  
        }  
    }  
}