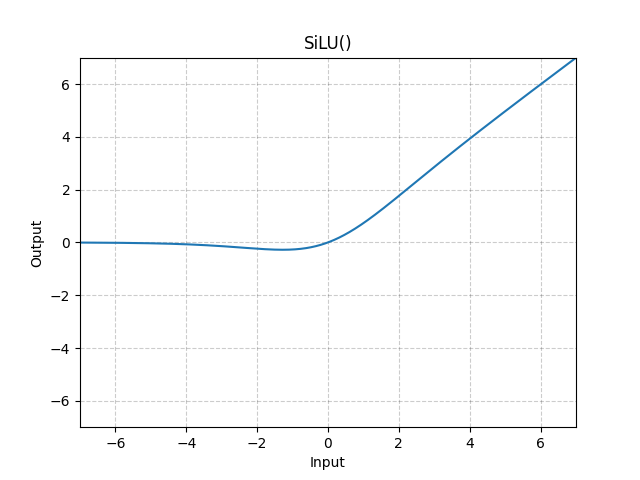
yolov8에서 사용한 Activation Function은 ReLU(), Leaky ReLU()도 아닌 SiLU()이다. 논문에선 Swish로 표현을 하였고 입력값에 sigmoid를 곱한 형태인데, 이 영향력이 파괴적이었다.
Swish paper : https://arxiv.org/pdf/1710.05941v1
1. Introduction
Activation Function은 딥러닝에서 학습의 성공을 위해서 주요한 역할을 한다. 2012년에 발표된 ReLU는 기존의 Supervisied training(비지도 학습)에 엄청난 영향을 주게 된다. ReLU Activation Function은 Sigmoid, Tanh보다 쉽게 최적화될 수 있어으며 단순하고 효과적이었다. ReLU Activation Function은 Default Activation Function으로 자리매기기 시작했다.
ReLU를 대체하기 위해 많은 연구들이 쏟아져 나오기 시작했다. 하지만 단순하고 실현성이 높으며 뛰어난 성능을 보여주는 RelU를 이기긴 힘들었다.
그래서 우리는 ReLU의 대항마인 Swish Activation Function을 고안했다. input에 sigmoid를 곱한 형태인 f(x) = x * sigmoid(x)인 부드러운 비선형함수이다.
2. Swish
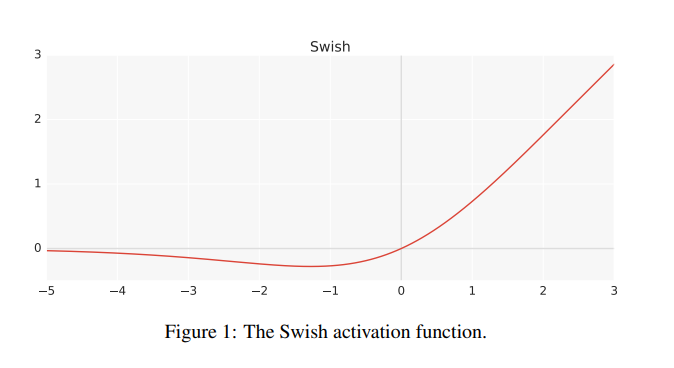
위의 Activation Function의 이름은 Swish Activation Fucntion이다. 일례로 sigmoid function을 derivative한다고 했을때, Chain Rule에 의거하여 구할 수 있는데
sigmoid'(x) = sigmoid(x)(1 - sigmoid(x))의 값으로 표현할 수 있다.
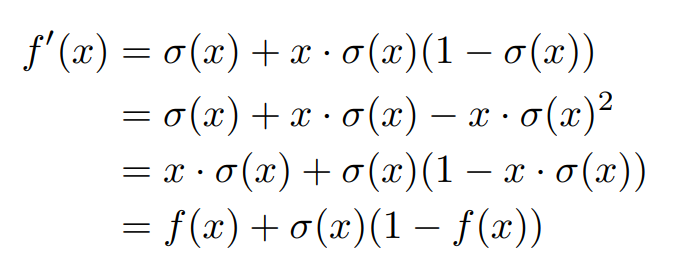
Swish의 경우 input값을 더하는 과정이 필요하다 보니 앞에 sigmoid값이 더 붙게 되는데, 이는 연산량이 늘어나는 대신 더 높은 performace를 낸다고 볼 수 있지 않을까? 그리고 형태가 뭔가 매우 비슷하다.
** ReLU의 derivative는 매우 극단적이다(step function과 같아짐). backpropagation을 통해 한번의 ReLU를 통과하면 input값이 0보다 작으면 0을 0보다 크면 1을 출력한다. Network의 깊이가 매우 깊어도 backpropagation을 진행하면서 derivative로 인한 gradient의 소실은 없다는 것을 의미한다.
activation function의 역사를 보면 linear function을 먼저 사용하다가 sigmoid를 사용했었는데, sigmoid의 단점은 Backpropagation을 통해 계속해서 Chain Rule을 진행하다 보니 Backpropagation에서 처음 들어온 input값이 여러 번의 derivative를 하게 되는데, output 값이 계속해서 작아지는 문제가 발생했다. 즉, 신경망이 깊으면 깊을수록 학습이 잘되어야 하는데, vanishing gradient가 발생하여 오히려 학습이 덜 되는 현상이 발생한다. 하지만 ReLU는 여러번 미분을 당해도 0보다 작으면 0, 0보다 크면 1을 출력하니 Activation Function으로 인한 gradient 소실은 없게되는데, 미분을 해서 0보다 작으면 0을 출력하고 0보다 크면 1을 출력하다보니 backpropagation의 시점으로 본다면 온전히 input과 weight간의 내적으로 인한 결과값으로만 output이 좌지우지 되는 것 같다. Backpropagation을 시점으로만 본다면 activation function의 큰 장점이 없는 것 같은,,? Activation이 나타내는 표현력이 없어진 것 같은 느낌이 든다.
Swish를 한번 derivative와 두번 derivative를 한다면 다음과 같은 결과를 얻을 수 있다.
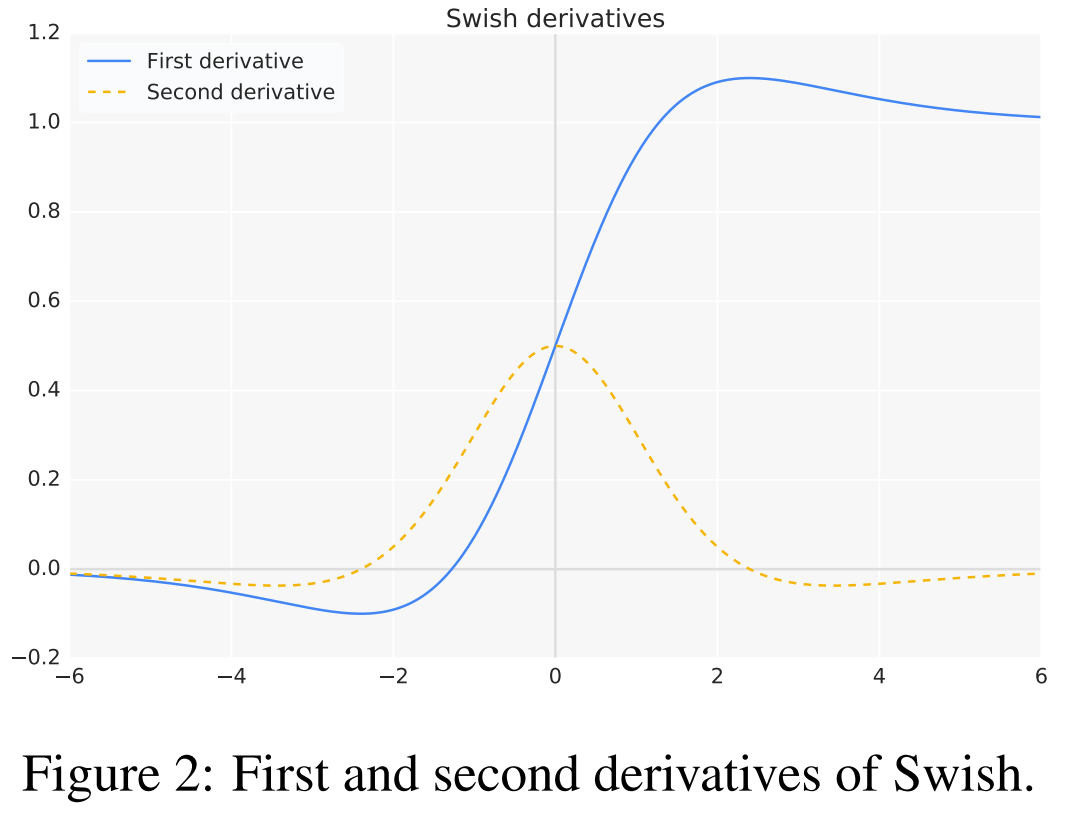
2.1 PROPERTIES OF SWISH
이 sector에서 가장 중요한 부분은 이 말인 것 같다.
Unboundedness is desirable because it avoids saturation, where training is slow due to near-zero graidents.
즉, 무한함은 gradient가 0으로 수렴하여 천천히 학습되는 포화상태를 피할 수 있기에 많은 연구가 되었다. 여기서 saturation이라 하면 sigmoid를 떠올릴 수 있는데, 출력에 제한을 둔 것을 의미한다.
sigmoid를 derivative를 하게 된면 위의 swish를 두번 derivative한 모양과 같게 나오는데, 0에 가까우면 gradient는 0에 convergence하고 1에 가까우면 gradient는 0에 convergence하게 된다. 즉, 입력값이 중요한 feature가 아니던 맞던 activation function을 거치게 되면 gradient의 0에 convergence하게 되는 것인데, 이는 model의 expresssion을 잃게 만들며 vanishing gradient를 초래하여 원활한 학습을 방해한다. 이 때문에 unboundedness가 매우 중요한 요소인데, ReLU의 경우에는 0보다 작으면 제한을 두지만 0보다 클 경우에는 unboundedness를 설정함으로써 이러한 문제를 해결했다는 것이 초점이다.
Swish도 이러한 ReLU의 Unboundedness의 properties를 가져와 사용했다는 것에 의미가 있다. 출력이 0보다 크다면 Unboundedness를 적용하여 ReLU의 properties를 가져왔다는 것.
또한, 앞에서 내가 언급했던 expressivity에 대해서도 말했는데, non-monotonicity를 통해 gradient flow(activation function에 들어가기 전의 입력값(preactivation))의 향상, 표현력을 증가시켰다는 것. 이 말이 의미하는 건 input과 weight의 inner product의 값이 음수여도 그 값을 출력하여 표현력을 높이는 데에 있다. (여긴 좀 더 이해가 필요할 듯.)
Smoothness에 대해서도 매우 중요하다고 저자는 말했는데, Linear, ReLU, Swish의 landscape를 보여주면서 설명한다.

Figure 5는 서로 다른 activation function을 사용하여 output landscape를 구현했다. 그들의 실험 내용은 초기 6개의 layer층에 랜덤하게 가중치를 초기화했으며 각 grid에 맞게 x, y coordinate를 통과시켰다. ReLU함수의 output landscape를 보면 마치 asterisk(* 표시와 같은 뾰쪽뾰족한 별모양)와 같은 표현력을 갖게 되어 부드러운 표현과는 멀다. 이와는 대조적으로 Swish activation fucntion은 부드러운 output landscape를 갖는다. 부드러움이 중요한 이유는 output landsacpe의 부드러운 표현력이 loss landscape의 표현력에도 엄청난 영향을 준다는 것이다. 부드러운 loss landscape가 learning rate와 initailize의 민감도를 줄이고 보다 쉽게 optimize할 수 있게 만들어준다.
그 뒤의 내용은 실험에 대한 내용이라 패스.
요약하자면 Swish Activation Function은 ReLU의 properties를 갖으나 smoothness를 부각시킨 activation function이다. ReLU가 표현하는 제한없는 properties로 saturation을 막고 smoothness를 통해 ReLU가 표현할 수 없는 표현력으로 loss 또한 부드럽게 convergence할 수 있도록 도와준다.
단, Swish Activation에도 단점이 있는데, 결국엔 여러번 미분하게 되면 saturation이 되는 거 아닐까? residual의 방식으로 x를 더하는 건 아니라 곱하는거지만 activation을 여러번 거치게 되면 표현력을 잃어가는 건 맞는 것 같다. 그래서 깊은 신경망에 사용하는 것보단 경량화 모델에 사용하는 것이 좋을 것 같고 모든 layer에 다 사용하는 것보단 Backbone에 사용했으면 neck이나 head부분에도 동일하게 사용하는 것까진 생각해볼 필요성이 있다.
또한, ReLU나 Leaky ReLU보다 연산량이 좀더 많기 때문에, 정말 메모리가 부족한 디바이스에선 사용하지 않는 것이 좋아보일수도? 이건 Yolov8을 좀더 분석하고 코드를 짜보면서 열심히 생각해 봐야할듯함.