3D U-Net은 의료 영상 분석, 특히 3D 볼륨 데이터(예: MRI나 CT 스캔)에 적합하도록 설계된 U-Net의 변형입니다.
기본 U-Net이 2D 이미지에 초점을 맞춘 반면, 3D U-Net은 3차원 데이터를 처리할 수 있도록 확장되었습니다. 이 모델은 3D 이미지의 분할을 위해 개발되었으며, 각 픽셀(또는 복셀)에 레이블을 할당하여 볼륨 데이터 내의 관심 영역을 구분합니다.
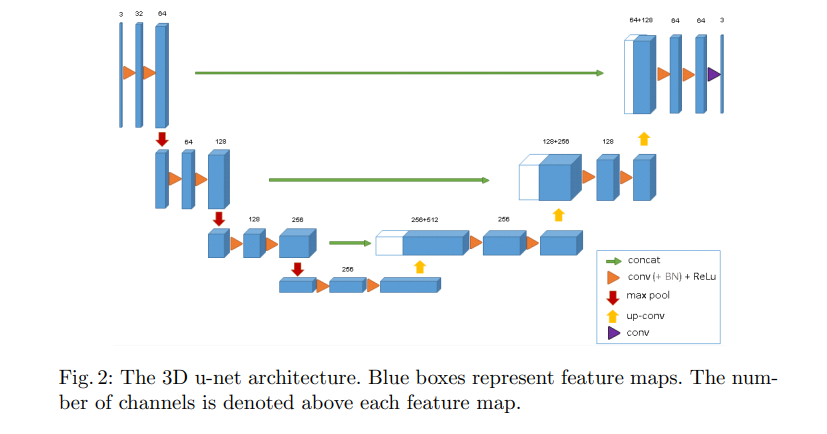
3D U-Net의 주요 구성 요소:
-
3D 컨볼루션: 2D U-Net에서 사용되는 2D 컨볼루션 대신, 3D U-Net은 3차원 데이터를 처리하기 위해 3D 컨볼루션을 사용합니다. 이는 3D 데이터에서의 깊이 정보를 포함하여 공간적인 정보를 학습합니다.
-
3D 맥스 풀링: 인코더(축소 경로)의 각 단계 후에는 3D 맥스 풀링이 적용됩니다. 이는 3차원 데이터의 크기를 줄이면서 중요한 특징을 유지합니다.
-
스킵 연결: 2D U-Net과 마찬가지로, 3D U-Net도 인코더의 각 단계에서 추출된 특징 맵을 디코더의 상응하는 단계와 결합합니다. 이는 디코더에서 잃어버린 세부 정보를 다시 얻을 수 있도록 돕습니다.
-
3D 업샘플링: 디코더(확장 경로)에서는 업샘플링을 통해 데이터의 크기를 다시 증가시킵니다. 이 과정은 3D 트랜스포즈 컨볼루션(또는 3D 업샘플링)을 사용하여 수행됩니다.
-
최종 3D 컨볼루션: 마지막 단계에서는 1x1x1 3D 컨볼루션을 사용하여 원하는 출력 채널 수로 특징 맵을 매핑합니다. 이는 각 복셀에 대한 분할 클래스 확률을 생성하는 데 사용됩니다.
3D U-Net의 응용:
3D U-Net은 주로 의료 영상 분석에 사용됩니다. 예를 들어, MRI 또는 CT 스캔에서 종양, 장기, 또는 다른 해부학적 구조의 정확한 분할에 사용됩니다. 이러한 정밀한 분할은 진단, 치료 계획, 그리고 질병 모니터링에 중요한 정보를 제공합니다.
3D U-Net의 장점은 3차원 데이터의 모든 방향에서의 공간적 컨텍스트를 포착할 수 있다는 점입니다. 이는 2D 방식으로 처리할 때 발생할 수 있는 정보의 손실을 최소화하며, 더욱 정확한 분석을 가능하게 합니다.
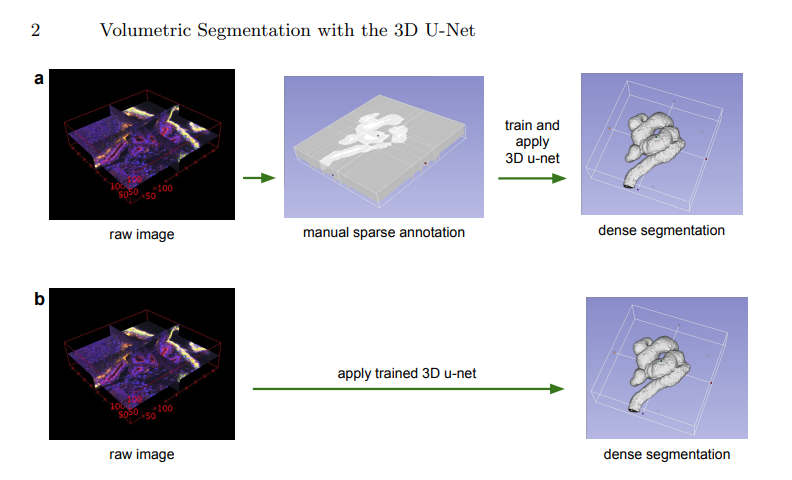
3D U-Net에서 사용되는 3D 컨볼루션, 3D 맥스 풀링, 그리고 3D 업샘플링은 각각 특정한 역할을 수행하며, 이러한 레이어들은 3D 영상 데이터를 효과적으로 처리하기 위해 설계되었습니다.
3D 컨볼루션
3D 컨볼루션은 2D 컨볼루션의 개념을 시간 또는 깊이 차원으로 확장한 것입니다. 전통적인 2D CNN이 여러 이미지 프레임을 처리한다면, 3D CNN은 공간적 및 시간적(또는 깊이적) 변화를 함께 분석할 수 있습니다. 3D CNN 아키텍처에는 입력 레이어, 다수의 컨볼루션 레이어, 활성화 함수, 맥스 풀링 레이어, 그리고 최종 분류 레이어가 포함됩니다. 컨볼루션 레이어는 입력에서 공간적 및 시간적/깊이적 특징을 학습하고 추출합니다
3D 맥스 풀링
3D 맥스 풀링 레이어는 3차원 입력을 입방형 풀링 영역으로 나누고, 각 영역의 최대값을 계산하여 다운샘플링을 수행합니다. 이 레이어는 공간적 차원에서 풀링을 수행하며, 3D 이미지 시퀀스의 경우 공간적 차원과 시간 차원 모두에서 풀링을 수행할 수 있습니다. 맥스 풀링은 중요한 특징을 유지하면서 특징 맵의 크기를 줄이고, 네트워크의 계산 효율성을 높입니다
3D 업샘플링
3D 업샘플링은 다차원 1D(시간적), 2D(공간적), 또는 3D(용적적) 데이터를 업샘플링합니다. 입력 데이터는 미니배치 x 채널 x [선택적 깊이] x [선택적 높이] x 너비의 형태로 가정됩니다. 업샘플링 알고리즘에는 가장 가까운 이웃, 선형, 이중선형, 삼중선형 등이 있으며, 3D, 4D, 5D 입력 텐서에 각각 적용됩니다. 업샘플링 시 scale_factor 또는 목표 출력 size 중 하나를 사용하여 출력 크기를 계산합니다
즉 기존의 2D 에서 진행되던 과정들에 Z축을 하나 추가해서 컨벌루전,맥스풀링,업샘플링을 진행 한 것이라 보면 됩니다.
