3D-UNET을 이용한 CT,MRI Image segmentation 1. 2D U-NET 과 VGG16

두번째 과제로 CT,MRI 이미지를 Segmentation 하는것이 목표입니다.
2D처럼 만만하게 봤다가 두들겨 맞았습니다.
UNet,VGG16,3D-UNet에 알아보며 어떻게 해야할지 알아봅시다.

U-Net

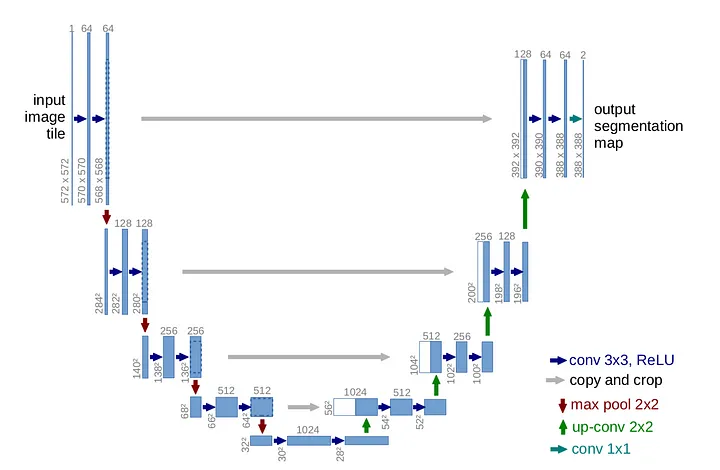
U-Net은 주로 의료 이미지 분할에 사용되는 네트워크로, 인코더-디코더 구조와 스킵 연결을 특징으로 합니다.

U-Net 구조

1. 인코더(Contracting Path):

   • 인코더는 여러 층의 컨볼루션(Convolution)과 맥스 풀링(Max Pooling) 연산으로 구성됩니다.

   • 컨볼루션 공식: $f(I, K) = (I * K) + b$, 여기서 $I$는 입력 이미지, $K$ 는 컨볼루션 커널, $b$는 편차(bias), $*$ 는 컨볼루션 연산을 나타냅니다.

   • 맥스 풀링은 region에서 가장 큰 값을 선택하여 이미지의 크기를 줄입니다.

2. 디코더(Expansive Path):

   • 디코더는 업샘플링(Up-sampling)과 컨볼루션 연산으로 구성됩니다.
   • 업샘플링은 입력 특징 맵의 크기를 증가시키는 과정입니다.
   • 업샘플링 후, 인코더에서의 대응하는 특징 맵과 결합(concatenation)하여 세부 정보를 복원합니다.

3. 스킵 연결(Skip Connections):

   • 인코더의 각 층에서 추출된 특징 맵을 디코더의 대응하는 층과 결합합니다.
   • 이를 통해 디코더가 잃어버린 세부 정보를 다시 얻을 수 있도록 합니다.

4. 최종 출력:

   • 네트워크의 마지막에는 1x1 컨볼루션을 사용하여 원하는 분할 맵의 채널 수를 얻습니다.
   • 분할 작업에서는 소프트맥스(Softmax) 함수나 시그모이드(Sigmoid) 함수를 사용하여 각 픽셀의 클래스 확률을 계산합니다.

여기서 컨볼루션(Convolution)과 맥스 풀링(Max Pooling)은 신호 처리(signal processing)와 이미지 처리(image processing)에서 널리 사용되는 개념들입니다. 딥러닝, 특히 컨볼루셔널 신경망(CNN)에서 핵심적인 연산으로 사용되니 잠시 알아보도록 합시다.

1. 컨볼루션 (Convolution):

컨볼루션은 신호 또는 이미지에 대한 필터링 작업으로 이해할 수 있습니다. 신호 처리에서 컨볼루션은 두 신호를 결합하여 새로운 신호를 생성하는 과정을 의미합니다.
이미지 처리에서는 컨볼루션을 사용하여 이미지에 특정 필터(커널)를 적용하고, 이를 통해 이미지의 특징을 추출합니다.

• 수학적 정의: 이미지 $I$와 커널 $K$에 대한 컨볼루션은
  $(I * K)(i, j) = \sum_m \sum_n I(m, n) \cdot K(i-m, j-n)$로 표현됩니다.
  여기서 $(i, j)$는 이미지 상의 위치, $(m, n)$은 커널 상의 위치입니다.

• 시각적 이해: 커널이 이미지 위를 슬라이드하며 각 위치에서 커널과 이미지의 원소 간의 곱셈을 수행하고, 이를 모두 합산합니다. 이 합산된 값이 결과 이미지의 해당 위치에 기록됩니다.

2. 맥스 풀링 (Max Pooling):

맥스 풀링은 이미지의 부분 영역에서 가장 큰 값을 선택하여 새로운 축소된 이미지를 생성하는 과정입니다. 이는 이미지의 크기를 줄이면서도 중요한 특징을 유지하고자 할 때 사용됩니다.

• 수학적 정의: 주어진 영역(풀링 윈도우)에서의 맥스 풀링은 $M(x)(i, j) = \max_{m, n \in W} x(m, n)$로 정의됩니다. 여기서 $W$는 풀링 윈도우(Pooling Window) 를 나타냅니다.

• 시각적 이해: 풀링 윈도우가 이미지 위를 슬라이드하며 각 윈도우 내에서 가장 큰 값을 선택합니다. 이 값들로 구성된 새로운 이미지가 맥스 풀링의 결과가 됩니다.

시각화:

이제 컨볼루션과 맥스 풀링의 과정을 시각화 하면 다음과 같습니다.

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal

# 예시 이미지와 커널 생성
image = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16]
])

kernel = np.array([
    [1, 0],
    [0, -1]
])

# 컨볼루션 연산 수행
conv_result = scipy.signal.convolve2d(image, kernel, mode='valid')

# 맥스 풀링 연산 수행
pool_size = 2
maxpool_result = np.empty((image.shape[0]//pool_size, image.shape[1]//pool_size))
for i in range(0, image.shape[0], pool_size):
    for j in range(0, image.shape[1], pool_size):
        maxpool_result[i//pool_size, j//pool_size] = np.max(image[i:i+pool_size, j:j+pool_size])

# 결과 시각화
fig, axs = plt.subplots(1, 3, figsize=(15, 5))

axs[0].imshow(image, cmap='gray')
axs[0].set_title('Original Image')
axs[0].axis('off')

axs[1].imshow(conv_result, cmap='gray')
axs[1].set_title('Convolution Result')
axs[1].axis('off')

axs[2].imshow(maxpool_result, cmap='gray')
axs[2].set_title('Max Pooling Result')
axs[2].axis('off')

plt.show()

1. 원본 이미지: 4x4 픽셀 크기의 간단한 예시 이미지입니다. 각 픽셀의 값은 1부터 16까지 증가합니다.

2. 컨볼루션 결과: 여기서는 2x2 크기의 커널을 사용하여 컨볼루션을 수행한 결과입니다. 원본 이미지에 커널을 적용하여, 커널과 겹치는 각 영역에서의 픽셀 값의 가중 합을 계산합니다.

3. 맥스 풀링 결과: 맥스 풀링은 2x2 크기의 윈도우를 사용하여 각 영역에서 가장 큰 값을 선택합니다. 결과적으로 이미지의 크기가 줄어들지만, 주요 특징(큰 값)은 유지됩니다.

U-Net 구현:

import torch
import torch.nn as nn

class UNet(nn.Module):
    def __init__(self, in_channels=1, out_channels=2):
        super(UNet, self).__init__()

        # Contracting Path
        self.down1 = self.contracting_block(in_channels, 64)
        self.down2 = self.contracting_block(64, 128)
        self.down3 = self.contracting_block(128, 256)
        self.down4 = self.contracting_block(256, 512)
        self.down5 = self.contracting_block(512, 1024)

        # Expansive Path
        self.up4 = self.expansive_block(1024, 512)
        self.up3 = self.expansive_block(512, 256)
        self.up2 = self.expansive_block(256, 128)
        self.up1 = self.expansive_block(128, 64)

        # Final output layer
        self.final = nn.Conv2d(64, out_channels, kernel_size=1)

    def contracting_block(self, in_channels, out_channels):
        block = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=2, stride=2)
        )
        return block

    def expansive_block(self, in_channels, out_channels):
        block = nn.Sequential(
            nn.ConvTranspose2d(in_channels, out_channels, kernel_size=2, stride=2),
            nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1),
            nn.ReLU(inplace=True)
        )
        return block

    def forward(self, x):
        # Contracting Path
        x1 = self.down1(x)
        x2 = self.down2(x1)
        x3 = self.down3(x2)
        x4 = self.down4(x3)
        x5 = self.down5(x4)

        # Expansive Path
        x = self.up4(x5)
        x = torch.cat([x4, x], dim=1)
        
        x = self.up3(x)
        x = torch.cat([x3, x], dim=1)
        
        x = self.up2(x)
        x = torch.cat([x2, x], dim=1)
        
        x = self.up1(x)
        x = torch.cat([x1, x], dim=1)

        # Final Convolution
        x = self.final(x)
        return x

# Create the model
model = UNet(in_channels=1, out_channels=2)
print(model)

1채널 입력과 2채널 출력을 가정하는 모델입니다

예시 설명

예를들어 128x128 사이즈의 이미지가 존재하고 (30,40) (60,70) 부분이 segment 해야하는 feature이라 가정해보고

채널은 64, 128, 256, 512로 증가하고, 다시 256, 128, 64로 감소한다고 가정할 때, 각 단계에서 이미지는 다음과 같이 처리됩니다:

인코더 (Contracting Path):

1. 초기 컨볼루션 (64 채널): 128x128 크기의 입력 이미지가 두 개의 연속적인 3x3 컨볼루션 레이어를 거칩니다. 여기서는 64개의 특징 맵이 생성됩니다. 이미지의 크기는 패딩이 적용되지 않았다면 감소할 수 있습니다 (예: 126x126).

2. 맥스 풀링과 두 번째 컨볼루션 (128 채널): 첫 번째 컨볼루션 레이어 다음에 2x2 맥스 풀링이 적용되어 이미지의 크기는 절반으로 줄어듭니다 (예: 64x64). 그 다음에 128개의 특징 맵을 생성하는 두 번째 컨볼루션 레이어가 적용됩니다.

3. 추가 맥스 풀링과 컨볼루션 (256 채널, 512 채널): 이미지의 크기를 계속 줄여가면서 특징 맵의 수를 증가시킵니다. 각 단계에서 이미지의 크기는 절반으로 줄어들고, 특징 맵의 수는 두 배가 됩니다.

디코더 (Expansive Path):

1. 업샘플링과 첫 번째 컨볼루션 (512 채널 → 256 채널): 인코더의 최종 단계에서 생성된 특징 맵을 업샘플링하여 이미지의 크기를 증가시킵니다 (예: 16x16 → 32x32). 그 다음 인코더의 해당 단계에서 복사된 특징 맵과 결합하고, 256개의 특징 맵을 생성하는 컨볼루션 레이어를 적용합니다.

2. 추가 업샘플링과 컨볼루션 (256 채널 → 128 채널, 128 채널 → 64 채널): 이 과정은 계속해서 업샘플링과 컨볼루션을 통해 이미지의 크기를 늘리고 특징 맵의 수를 줄여가며, 인코더에서의 세부 정보를 복원합니다.

출력:

1. 최종 1x1 컨볼루션 (64 채널 → 2 채널): 마지막 단계에서는 1x1 컨볼루션을 사용하여, 각 픽셀에 대한 분할 예측을 위해 특징 맵의 수를 원하는 분할 클래스의 수로 줄입니다.

예를 들어, 이미지의 특정 위치 (30, 40)과 (60, 70)이 분할해야 하는 특징이라고 가정하면, 인코더에서는 해당 위치의 특징을 감지하고, 디코더에서는 해당 위치의

특징을 더 세밀하게 복원하게 됩니다. 스킵 연결은 인코더에서의 세부 정보를 디코더로 전달하여, 최종 분할 맵에서 해당 특징이 정확하게 재현될 수 있도록 도와줍니다.

더욱 자세한 설명은 다음을 참고하시면 좋습니다.
unet
convolution

VGG-16

VGG-16은 간단하면서도 깊은 컨볼루셔널 신경망(CNN) 구조로, 주로 이미지 분류 작업에 사용됩니다. VGG-16은 이름에서 알 수 있듯이 16개의 레이어로 구성되어 있으며, 여기에는 가중치를 가진 레이어(컨볼루션 및 완전 연결 레이어)가 포함됩니다.

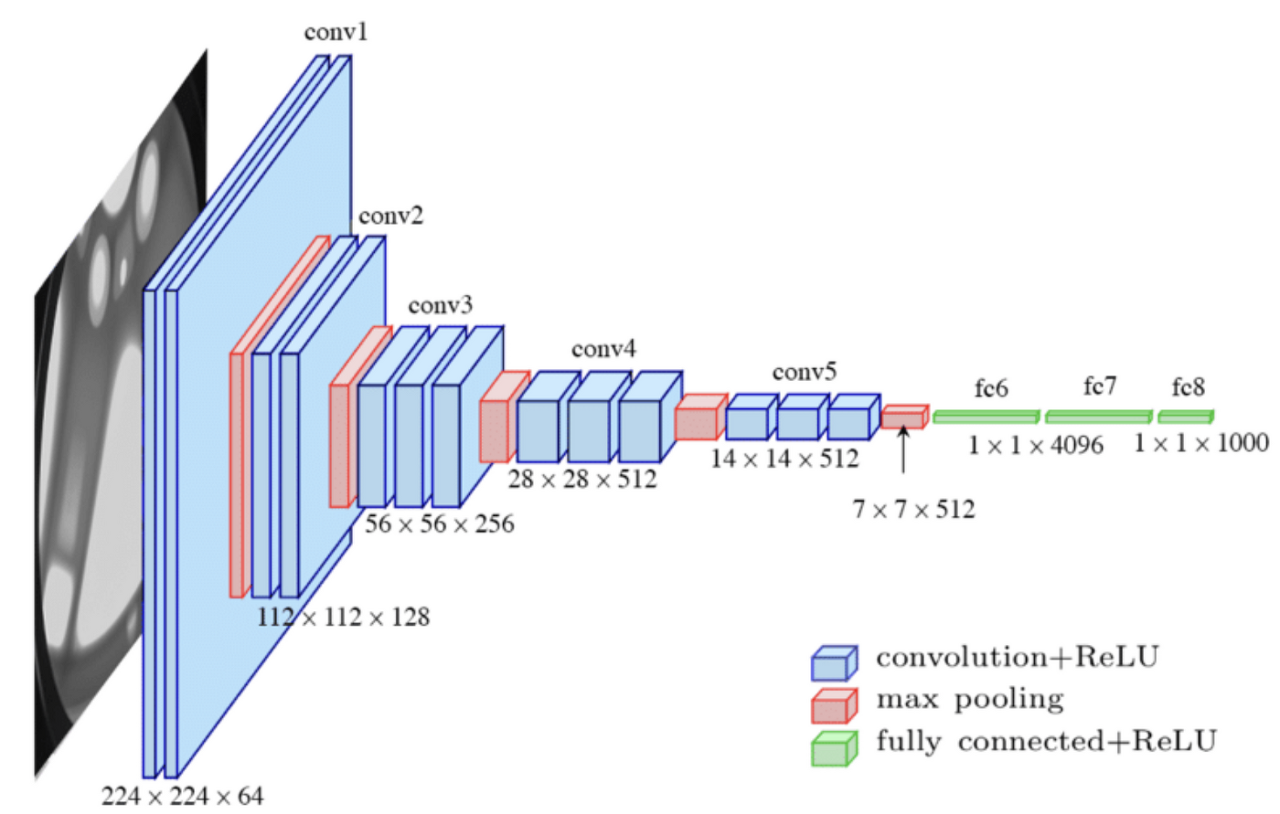
VGG-16 구조:

1. 컨볼루션 레이어: VGG-16은 3x3 크기의 작은 컨볼루션 필터를 사용합니다. 이 필터는 전체 네트워크에 걸쳐 일관되게 사용됩니다. 각 컨볼루션 레이어 후에는 ReLU 활성화 함수가 적용됩니다.

2. 풀링 레이어: 컨볼루션 레이어 그룹 후에는 보통 2x2 맥스 풀링 레이어가 오며, 이는 feature map 의 크기를 줄입니다.
   맥스 풀링은 가장 강한 특징을 유지하면서 이미지의 공간 크기를 축소합니다.

3. 완전 연결 레이어(FCN): 모든 컨볼루션 및 풀링 레이어를 거친 후, 특징 맵은 완전 연결 레이어로 펼쳐집니다. VGG-16에는 세 개의 완전 연결 레이어가 있으며, 처음 두 레이어는 각각 4096개의 노드를 가지고, 마지막 레이어는 클래스의 수에 해당하는 노드를 가집니다.

4. 소프트맥스 레이어: 마지막 완전 연결 레이어 후에는 소프트맥스 활성화 함수가 적용되어, 각 클래스에 속할 확률을 출력합니다.

예시:

이제 224x224 크기의 이미지가 있다고 가정하고 VGG-16을 통과하는 과정을 설명하겠습니다. 우리가 분류하려는 대상이 이미지 내의 (30, 40) 위치에 있고, 다른 대상이 (60, 70) 위치에 있다고 가정해봅시다.

1. 첫 번째 컨볼루션 블록: 이미지는 두 개의 3x3 컨볼루션 레이어를 거치며 64개의 특징 맵을 생성합니다. 이후 2x2 맥스 풀링으로 크기가 112x112로 줄어듭니다.

2. 두 번째 컨볼루션 블록: 이제 128개의 특징 맵을 생성하는 두 개의 컨볼루션 레이어를 거칩니다. 또 다시 맥스 풀링으로 크기가 56x56으로 줄어듭니다.

3. 세 번째 컨볼루션 블록: 256개의 특징 맵을 생성하는 세 개의 컨볼루션 레이어를 거친 후, 크기는 28x28로 줄어듭니다.

4. 네 번째 컨볼루션 블록: 512개의 특징 맵을 생성하는 세 개의 컨볼루션 레이어를 거치고, 이후 맥스 풀링으로 크기가 14x14로 줄어듭니다.

5. **다섯 번째 컨볼루션

   블록:** 또 다시 512개의 특징 맵을 생성하고, 맥스 풀링으로 크기가 7x7로 줄어듭니다.

6. 완전 연결 레이어: 이후 특징 맵은 Fully connected layer 로 펼쳐져서, 이미지 전체에서 추출된 고수준의 특징을 기반으로 분류를 수행합니다.

각 단계에서 (30, 40)과 (60, 70) 위치에 있는 대상의 특징은 점점 추상화되어 갑니다. 네트워크가 깊어질수록 위치 정보는 점점 덜 구체적이 되지만, 대신에 대상을 더 잘 분류할 수 있는 고수준의 정보가 추출됩니다. 최종적으로, 네트워크는 이러한 정보를 바탕으로 각 클래스에 속할 확률을 계산하여 분류합니다.

VGG-16 구현

import torch
import torch.nn as nn
class VGG16(nn.Module):
    def __init__(self, num_classes=10):
        super(VGG16, self).__init__()
        self.features = nn.Sequential(
            #1
            nn.Conv2d(3,64,kernel_size=3,padding=1),
            nn.BatchNorm2d(64),
            nn.ReLU(True),
            #2
            nn.Conv2d(64,64,kernel_size=3,padding=1),
            nn.BatchNorm2d(64),
            nn.ReLU(True),
            nn.MaxPool2d(kernel_size=2,stride=2),
            #3
            nn.Conv2d(64,128,kernel_size=3,padding=1),
            nn.BatchNorm2d(128),
            nn.ReLU(True),
            #4
            nn.Conv2d(128,128,kernel_size=3,padding=1),
            nn.BatchNorm2d(128),
            nn.ReLU(True),
            nn.MaxPool2d(kernel_size=2,stride=2),
            #5
            nn.Conv2d(128,256,kernel_size=3,padding=1),
            nn.BatchNorm2d(256),
            nn.ReLU(True),
            #6
            nn.Conv2d(256,256,kernel_size=3,padding=1),
            nn.BatchNorm2d(256),
            nn.ReLU(True),
            #7
            nn.Conv2d(256,256,kernel_size=3,padding=1),
            nn.BatchNorm2d(256),
            nn.ReLU(True),
            nn.MaxPool2d(kernel_size=2,stride=2),
            #8
            nn.Conv2d(256,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            #9
            nn.Conv2d(512,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            #10
            nn.Conv2d(512,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            nn.MaxPool2d(kernel_size=2,stride=2),
            #11
            nn.Conv2d(512,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            #12
            nn.Conv2d(512,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            #13
            nn.Conv2d(512,512,kernel_size=3,padding=1),
            nn.BatchNorm2d(512),
            nn.ReLU(True),
            nn.MaxPool2d(kernel_size=2,stride=2),
            nn.AvgPool2d(kernel_size=1,stride=1),
            )
        self.classifier = nn.Sequential(
            #14
            nn.Linear(512*7*7,4096),
            nn.ReLU(True),
            nn.Dropout(),
            #15
            nn.Linear(4096, 4096),
            nn.ReLU(True),
            nn.Dropout(),
            #16
            nn.Linear(4096,num_classes),
            )
        #self.classifier = nn.Linear(512, 10)
 
    def forward(self, x):
        out = self.features(x)
        #        print(out.shape)
        out = out.view(out.size(0), -1)
        #        print(out.shape)
        out = self.classifier(out)
        #        print(out.shape)
        return out

vgg16의 총 parameter은 대략 7100만개 입니다.
어지간한 그래픽카드로 돌리면 vram 용량부족으로 죽어버리는게 단점이네요.

FCN 에 대한 더욱 자세한 설명은 아래 링크를 참고하시길 바랍니다.