Grover’s Search algorithm

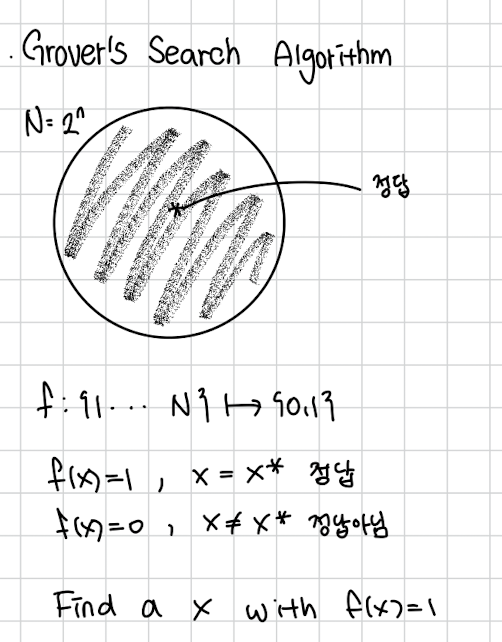
Grover Search 알고리즘은 정답을 확인하는 것은 쉬운데 가능한 경우의 수가 너무 많은 경우를 위한 알고리즘입니다. f(x)는 가능한 x를 넣으면 답이면 1을 답이 아니면 0 을 주는 함수입니다. 이 함수를 가지고 답을 찾고 싶습니다.

예를 들어 10000000가지 중에 1개가 정답이라고 해봅시다.
기존 컴퓨터는 이걸 일일이 해봐야 합니다.

Grover search는 이런 문제를 $\sqrt{N}$ 안에 해결합니다.
정답을 $x^*$이라고 하겠습니다.

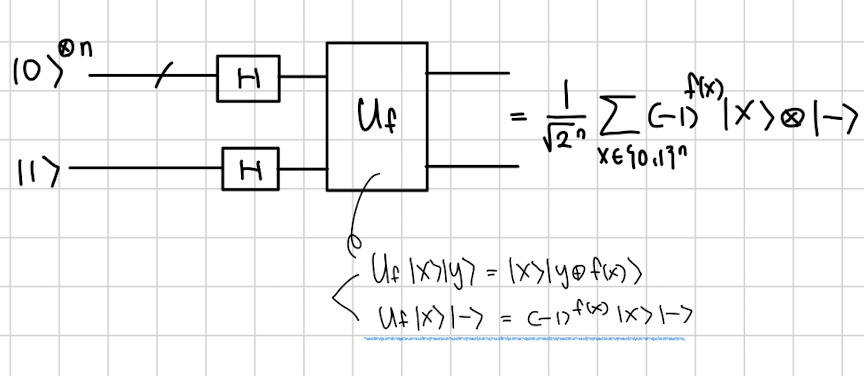
회로는 별거 없습니다. 기존과 똑같이 n 비트의 superpostion을 만들고
$\lvert - \rangle$ 와 Uf에 넣으면 저렇게 됩니다.
Uf를 넣으면 저렇게 되는 건 다음 공식을 이용한겁니다.

여기까지는 기존과 똑같습니다.
여기서 이제 새로운 유니터리를 적용하는데요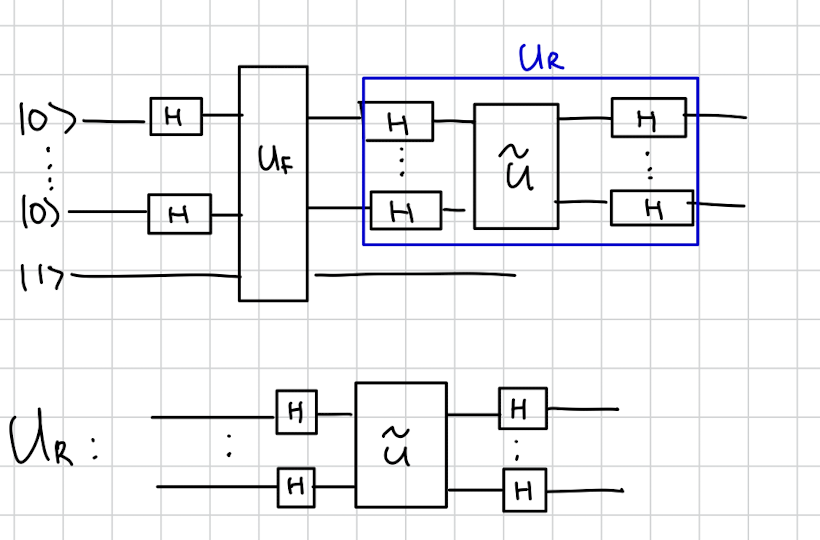
다음과 같이 $U_R$이라는 유니터리를 적용하게 됩니다.

$U_R$은 별거 없고 다음과 같습니다.
$= 2 \left( \lvert + \rangle^{\otimes n} \langle + \rvert^{\otimes n} \right) - I$

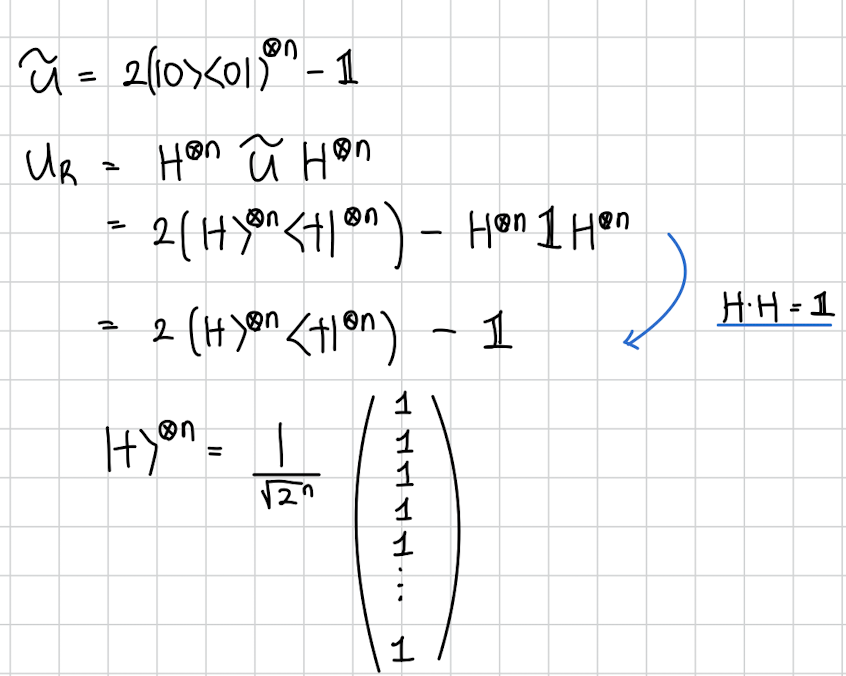
여기서 중요한건 $\lvert + \rangle^{\otimes n}$ 이 벡터에서 어떻게 생겼는가 입니다. 정의에 대해 생각해보면 저 애는 모든 가능한 n bit 상태를 다 균일하게 포함하고 있는 상태이기 때문에 생각보다 간단히 저렇게 모두가 $111 ... 11$ 인 벡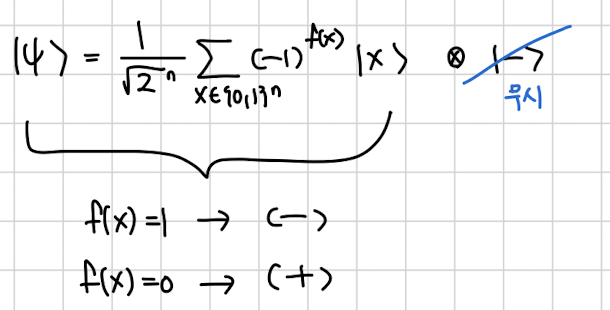터가 됩니다 .
이제 원래 상태에 $U_R$ 을 적용하고 싶은데요.
원래 상태를 좀 더 살펴보면 $f(x)$가 부호를 결정하는데 중요한건 $f(x)$는 정답에서만 1입니다. 그래서 정답인 부분만 마이너스가 되어버립니다. 마지막 마이너스 상태는 앞으로 아무일도 안하기 때문에 무시해도됩니다.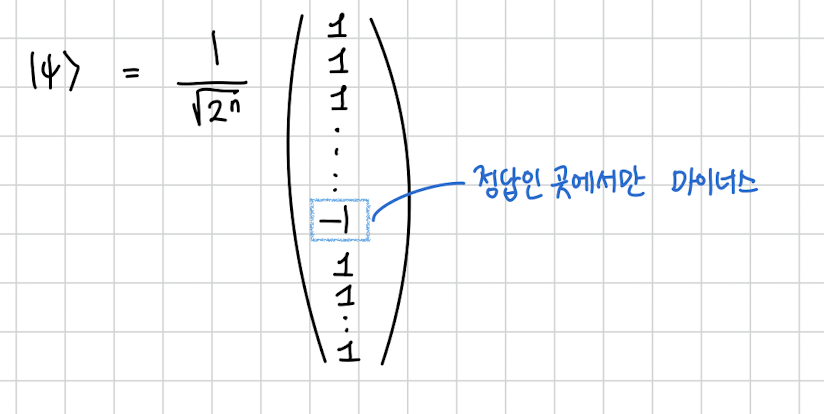
그래서 얘도 벡터 상태로 생각해보면 이렇게 표현할 수 있습니다.
$\lvert + \rangle^{\otimes n}$ 과 완전히 동일하지만 정답부분만 마이너스 입니다.

그리고 이게 우리의 상태에 $U_R$ 을 적용한 결과입니다.
수식을 보기 전에 그림으로 이해하면 더 쉽습니다.

이 식을 하나하나 그림으로 뜯어봅시다.

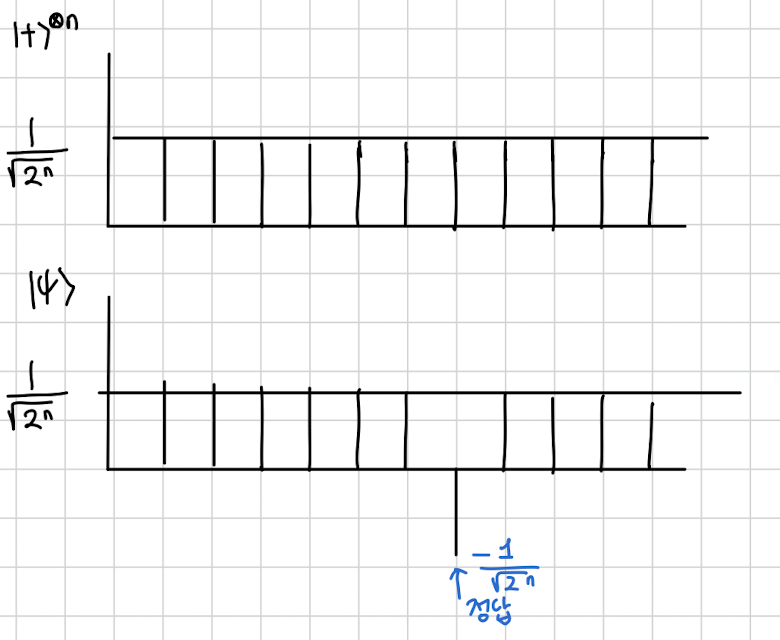
일단 이 그림은 쉽게 이해할 겁니다. $\lvert + \rangle^{\otimes n}$ 는 모두 균일한 높이고 $\lvert \psi \rangle$ 는 거기서 정답만 마이너스로 뒤집힌 상태입니다.
그리고 알파값에 대해서는 이렇게 생각할 수 있습니다. $\lvert \psi \rangle$의 높이들의 평균으로요. 그럼 마이너스가 섞여있기 때문에 원래 높이보다는 조금 더 작은 값이 알파일 것입니다.

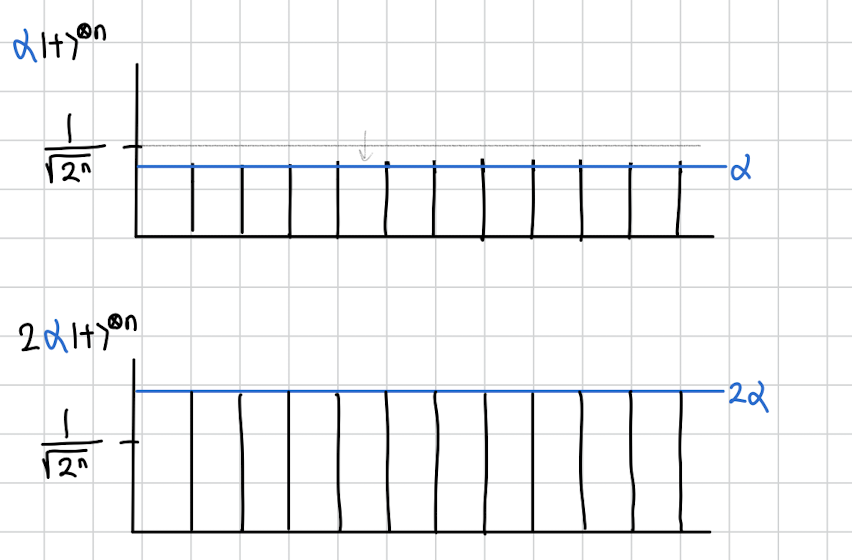
그림으로 보면 $2\alpha \lvert + \rangle^{\otimes n} - \lvert \psi \rangle$ 이 수식에서 $2\alpha \lvert + \rangle^{\otimes n}$ 여기까지는 이 그림과 같을 것입니다.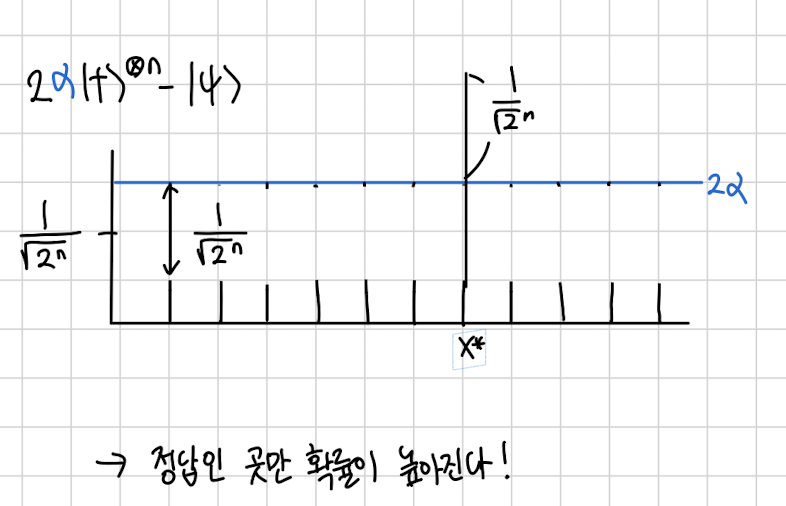
이제 여기서 수식의 나머지인 $- \lvert \psi \rangle$를 해주면 이렇게 마이너스인 부분은 플러스로 되어서 정답인 부분은 오히려 길이가 늘어나고 다른 곳은 그대로 마이너스가 되어서 짧아질 것 입니다.
이렇게 정답인 부분의 확률이 확 늘어나게 됩니다. !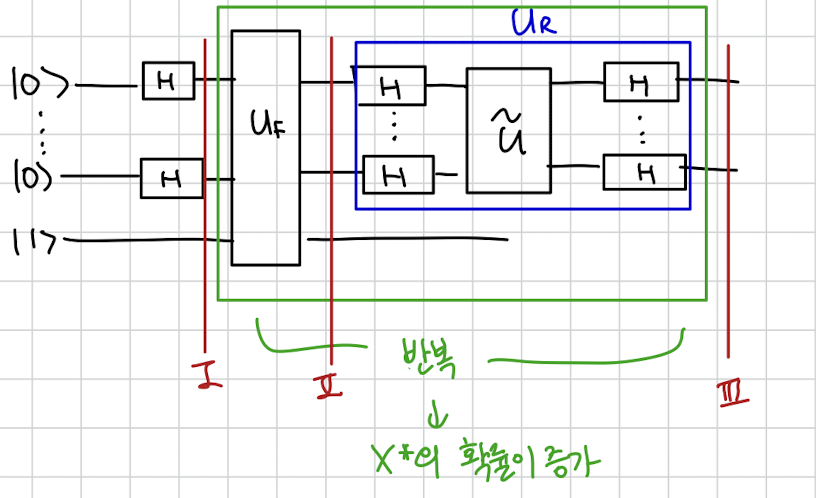
그리고 만약 이 과정을 몇번 반복하면 어떻게 될까요??
아마 계속 정답인 부분이 늘어나고 다른 부분은 계속 짧아져 측정을 하면 거의 정답만 측정이 될 겁니다.

수식으로 보자면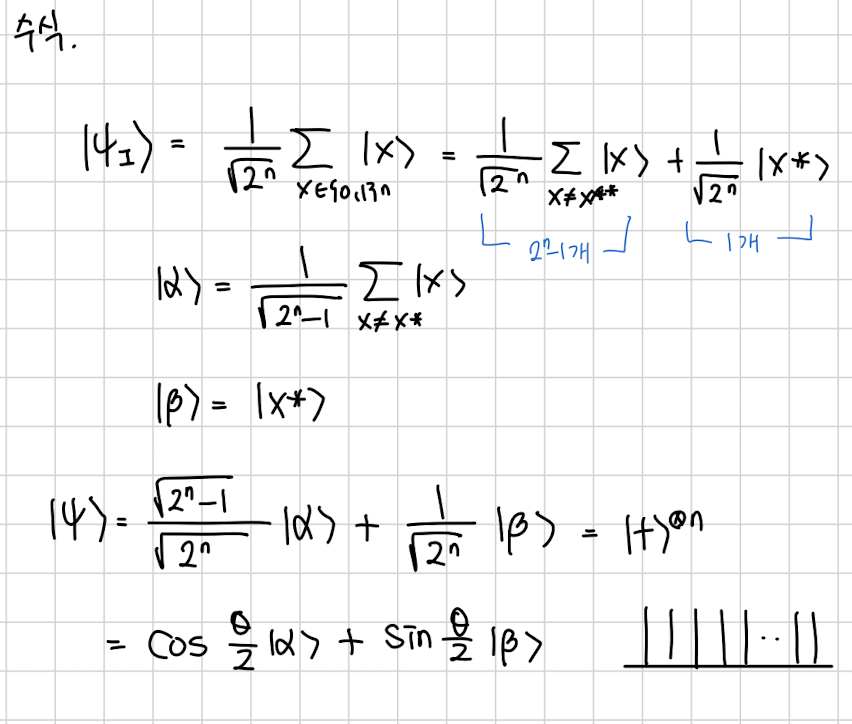


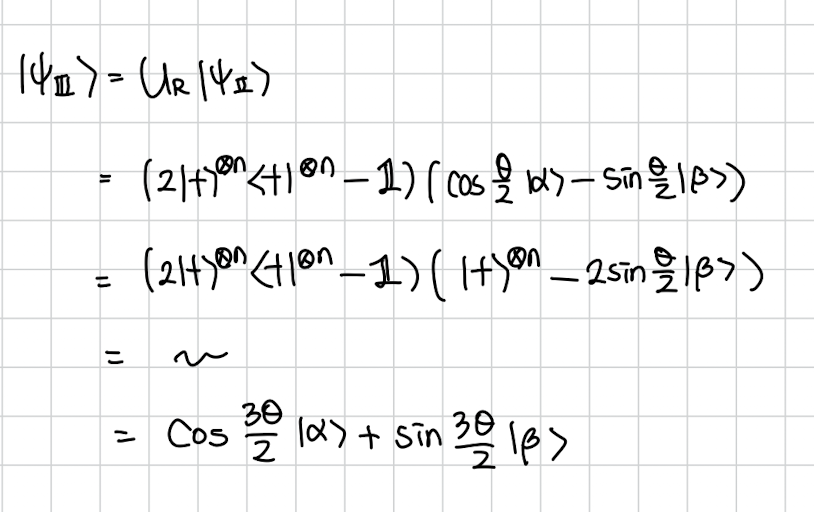
과정은 생략하고
$\cos\left(\frac{\theta}{2}\right) \lvert \alpha \rangle + \sin\left(\frac{\theta}{2}\right) \lvert \beta \rangle$ 가 \cos\left(\frac{3\theta}{2}\right) \lvert \alpha \rangle + \sin\left(\frac{3\theta}{2}\right) \lvert \beta \rangle$$
이렇게 변합니다.
이 뜻을 삼각함수로 보자면 각도를 점점 늘려서 사인 값을 늘리는 거라고 생각할 수 있습니다.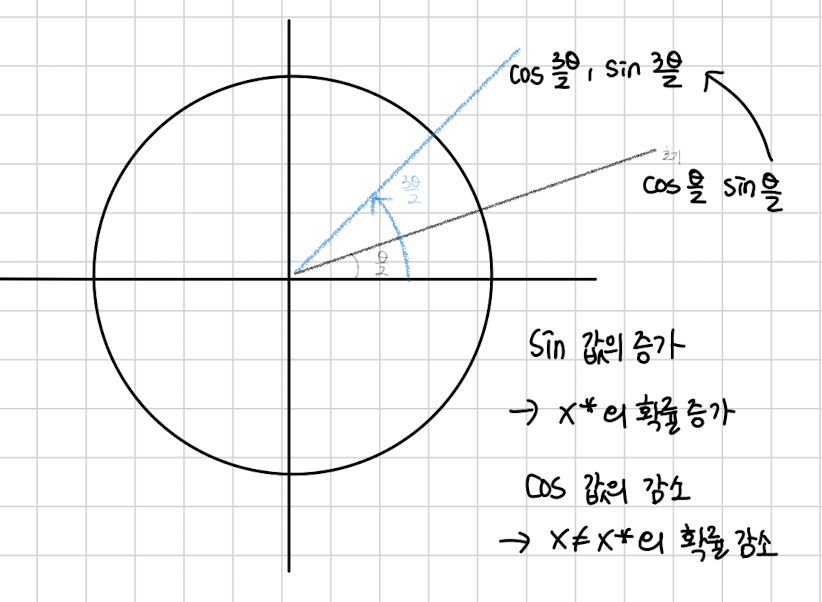
그런데 여기서 알 수 있는게 그럼 너무 과도하게 반복해서 각도를 너무 늘리면 어떻게 될까요,,? 아마 다시 사인값은 줄어들것입니다.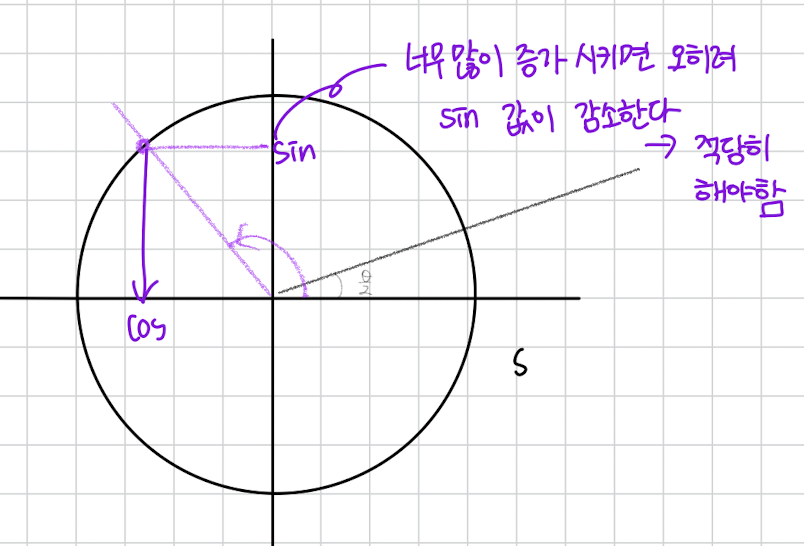

그럼 과연 몇번을 해야 될까요? 아마 sin 안에 각도가 $\frac{\pi}{2}$ 가 되도록 하면 될겁니다. 그럼 정답이 측정될 확률이 1에 가까워질거에요.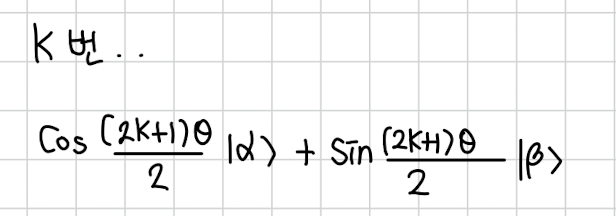
k번 반복할 때 각도는 이처럼 되고 이게 $\frac{\pi}{2}$ 와 같다고 하고 수식을 풀면
대충 K는 $\frac{\pi}{4} \quad \sqrt{N}$ 만큼 반복하면 됩니다.