양자컴퓨팅 기초

it is impossible to create an independent and identical copy of an arbitrary unknown quantum state. No cloning Theorem은 임의의 퀀텀 상태를 복제할 수 없다는 뜻입니다.

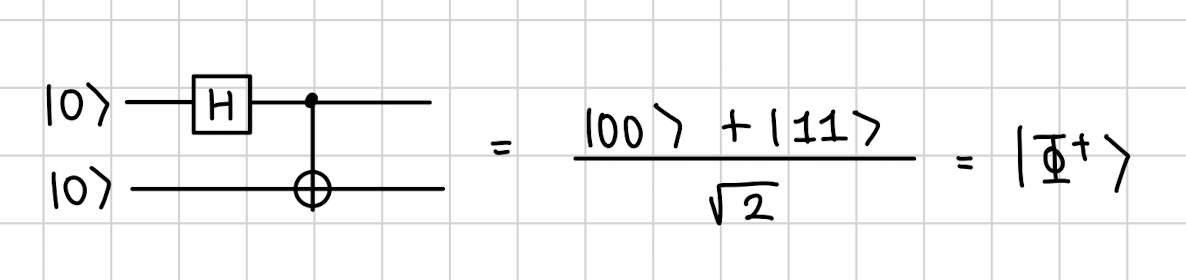
Alice와 Bob은 예전에 만났지만 지금은 떨어져 살고있다.옛날에 같이 Bell state 를 만들고 첫번째 비트는 Alice가 두번째 비트는 Bob이 나눠 가졌다. Alice는 Bob에게 임의의 퀀텀 상태를 전송하고 싶다. 하지만 Bob이 어디에 있는지 알 수 없다

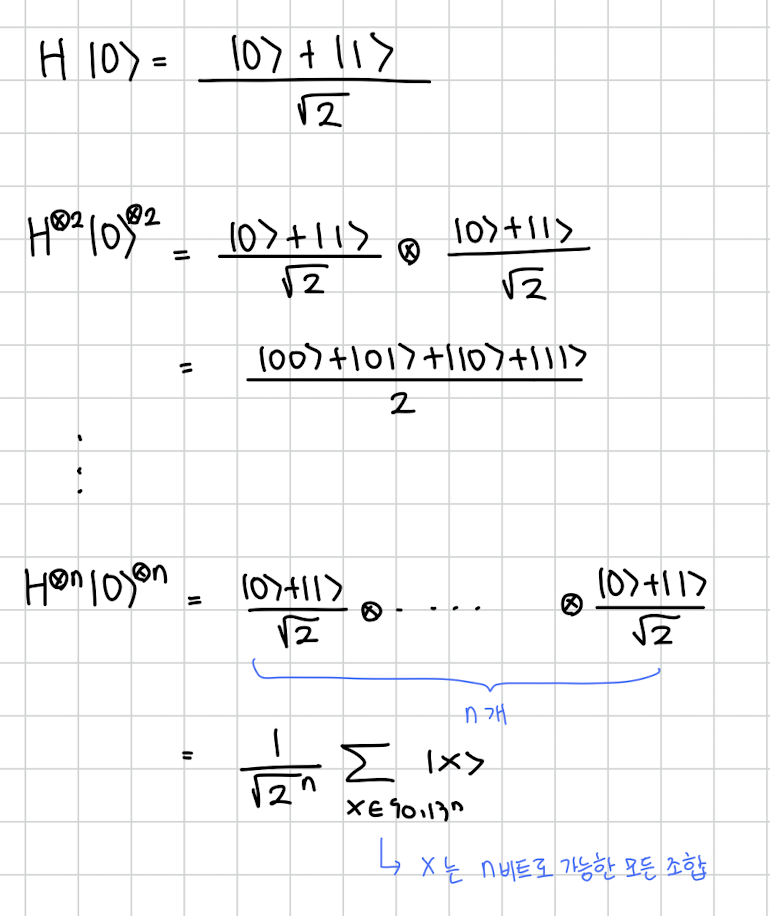
Quantum Parallelism 은 모든 가능한 연산을 동시에 할 수 있다는 개념입니다. 클래식은 N 가지 방법이 있으면 차례대로 N번 시도해야하죠. 하지만 퀀텀컴퓨팅에서는 N가지 방법이 있다면 이걸 한번에 다 동시에 연산을 할 수 있습니다.앞으로 나올 알고리즘들에

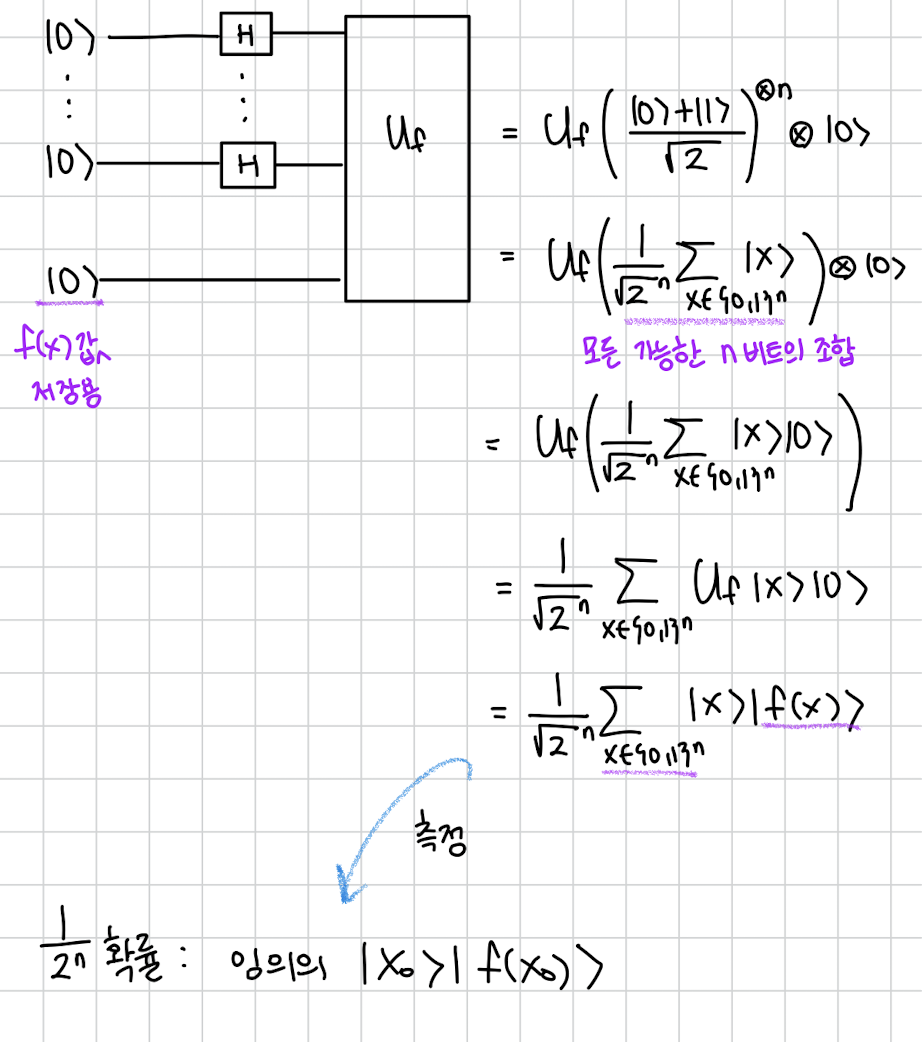
이렇게 간단한 함수 $f$가 있다고 할 때 $$ f : \{0, 1\} \mapsto \{0, 1\} $$ $f(0) =f(1)$ 인지 $f(0) \neq f(1)$ 구분하는 법은 뭘까? 원래는 간단하게 $f(0)$ 과 $f(1)$ 을 둘다 구해서 비교하는 법

DJ 알고리즘은 다음과 같은 상황을 해결해줍니다. 예를들어 $$f : \{0, 1\}^n \mapsto \{0, 1\}$$ 같은 함수가 있다고 합니다. 그런데 이 함수는 딱 두가지 경우라고 합니다. 모든 값이 같은 상수 함수거나 , 절반은 0 절반은 1 인 balan

BV 알고리즘은 숨은 string s를 찾는 알고리즘이다. 다음과 같이 $f : {0,1}^n \\mapsto {0,1}$ 가 있다고 하자 이 함수는 숨은 비밀 string s 와 내적값을 뱉어준다. $$f(x) = x \\cdot s,\\quad s \\in {0

Simons 알고리즘을 주기를 찾는 문제입니다. 다음과 같이 2 to 1 함수가 있다고 합시다. 2 to 1 이란건 항상 두 인풋이 쌍으로 같은 값을 가리킨다는 뜻입니다. $$ f : \{0,1\}^n \rightarrow \text{any finite set} \

이번에는 Factoring 과 관련된 알고리즘입니다. 알고리즘 자체는 그냥 주기를 찾는거지만 이걸 이용해서 큰 수를 Factoring할 수 있습니다. 저번에 Simons 알고리즘이 한 $f(x_0)$를 관측했을 때 가능성이 있는 $x$가 두가지가 있어서 그 두 상태가 superposition 상태로 존재하게 된다는 걸 이용했는데 그 개념을 여기서도 이용합...

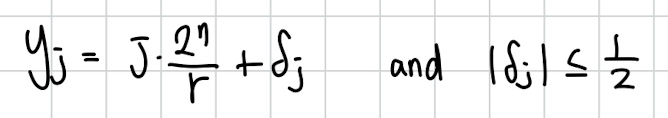
Shors algorithm 에서 y를 측정하고 그 y를 $2^n$으로 나눈것을 연분수 전개하면 우리가 r을 정확히 찾을 수 있다고 했습니다. 우리가 찾은 y는 40프로의 확률로 이 꼴을 띄게 됩니다. $\\frac{j}{r}$ 은 $\\frac{y_j}{2^n}$의

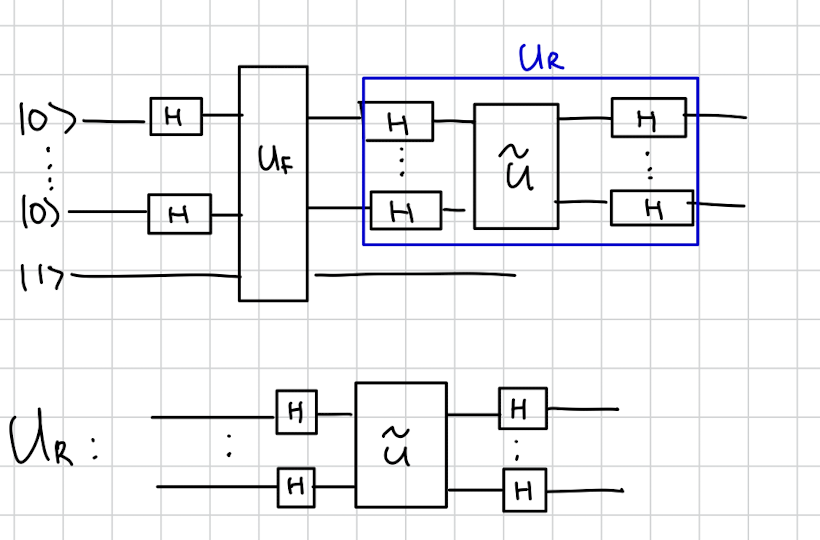
Grover Search 알고리즘은 정답을 확인하는 것은 쉬운데 가능한 경우의 수가 너무 많은 경우를 위한 알고리즘입니다. f(x)는 가능한 x를 넣으면 답이면 1을 답이 아니면 0 을 주는 함수입니다. 이 함수를 가지고 답을 찾고 싶습니다. 예를 들어 1000000

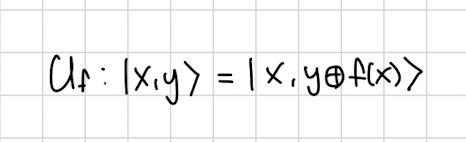
이제 까지 계속 알고리즘에 이 유니터리가 나왔는데요.구체적으로 어떻게 구현하는지 알아보려고 합니다. 우리가 어떤 임의의 매트릭스가 있을 때 그거의 원소를 확인하는 법은 무엇일까요?일단 다음과 같이 오른쪽에 0 벡터를 곱하면 0번째 열이 나옵니다. 1 벡터를 곱하면 1번