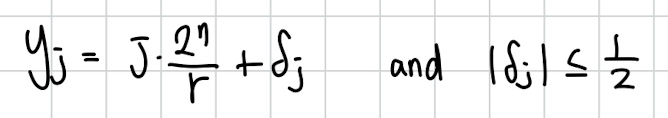Shor’s algorithm (2)

Shors algorithm 에서 y를 측정하고 그 y를 $2^n$으로 나눈것을 연분수 전개하면 우리가 r을 정확히 찾을 수 있다고 했습니다.

우리가 찾은 y는 40프로의 확률로 이 꼴을 띄게 됩니다.

$\frac{j}{r}$ 은 $\frac{y_j}{2^n}$의 연분수 전개에 부분합 형태로 나타난다고 합니다.

이거를 한번 예제를 풀어보려고 합니다.

일단 연분수 전개란 다음과 같은 꼴을 말합니다. 무한히 해나가는거죠.

그리고 $\frac{j}{r}$ 은 부분합 중 하나로 등장한다고 했는데 부분합은 다음과 같은걸 말합니다. 여기서 좋은건 $a_0, a_1, a_2 ...$ 들은 모두 양의 정수입니다. 그러니까 부분합 형태로 나타난단건 그냥 정수로 이루어진 분수를 계산하면 되어서 계산이 매우 간단합니다.

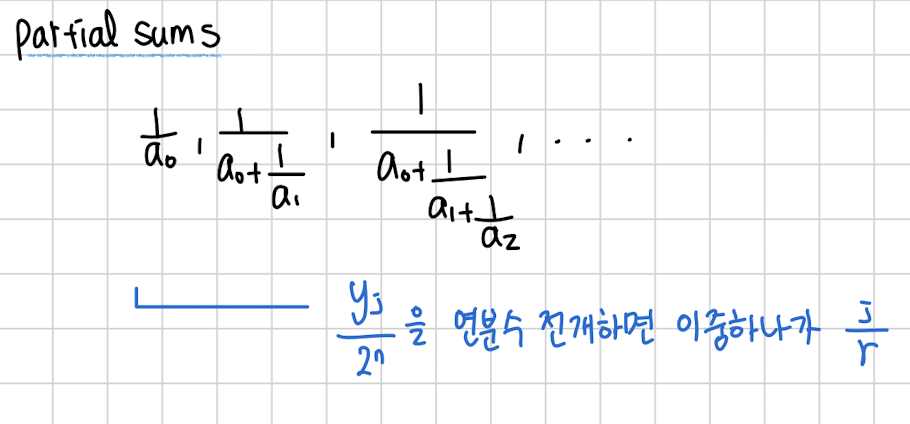
한번 연분수 전개를 직접해서 r을 찾아봅시다.

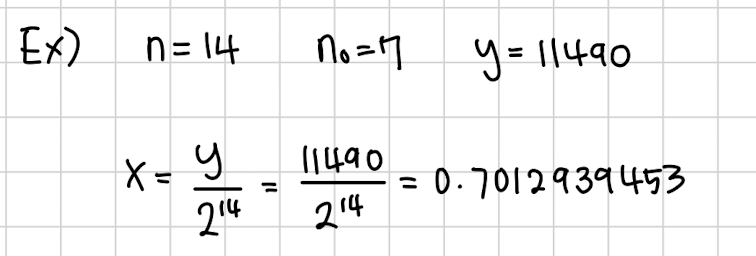
$n=2n_0$ 인걸 기억해야합니다. 그래서 $n=14$면 자동으로 $n0=7$이 됩니다.
그리고 일단 $y$를 $2^n$으로 나눠준 값을 구합니다. 우리는 이제 저 $x$를 연분수 전개하면 $\frac{j}{r}$ 이 나온다는걸 알고 있습니다.

연분수 전개를 한번 해봅시다.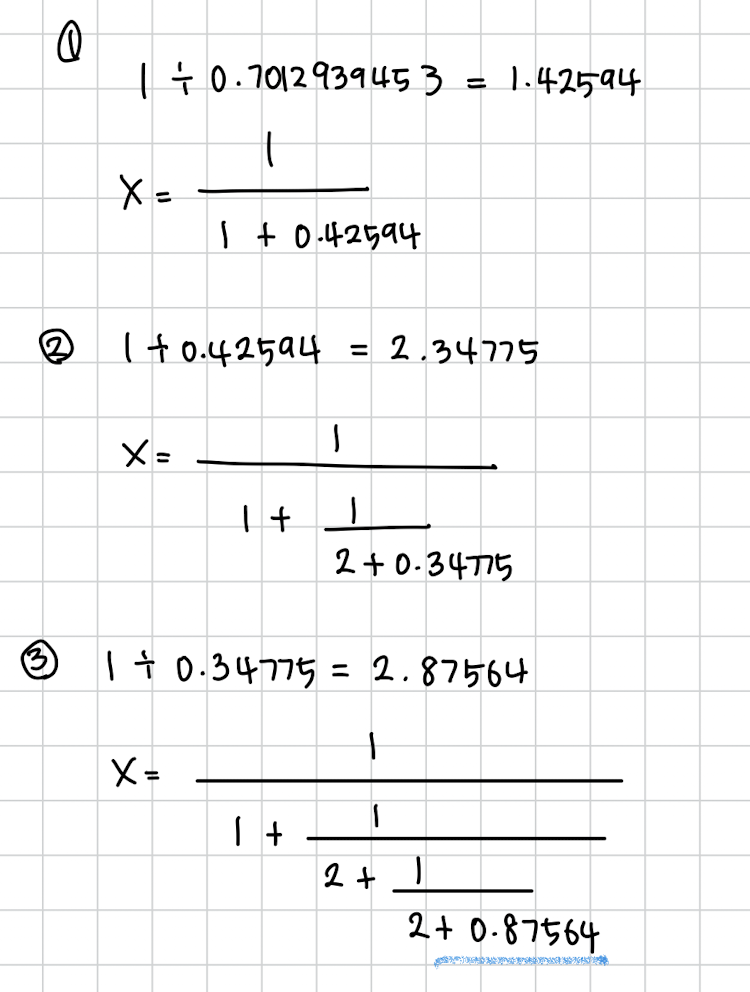

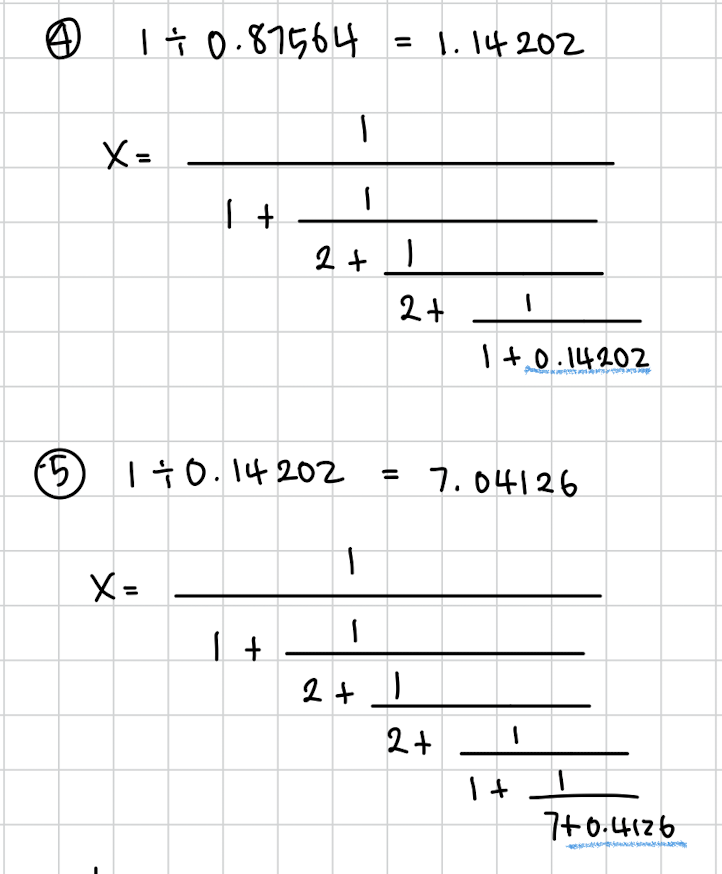
이렇게 됩니다. 이제 슬슬 멈출때도 된게 정수가 원래 2 1 2 1 만 나오다가 확 커졌죠? 이 정도면 보통 멈출때가 된겁니다. 한번 확인해봅시다.
확인하는 법은 조건을 만족하는지 확인하면됩니다. 어떤 조건이냐면 다음 조건입니다.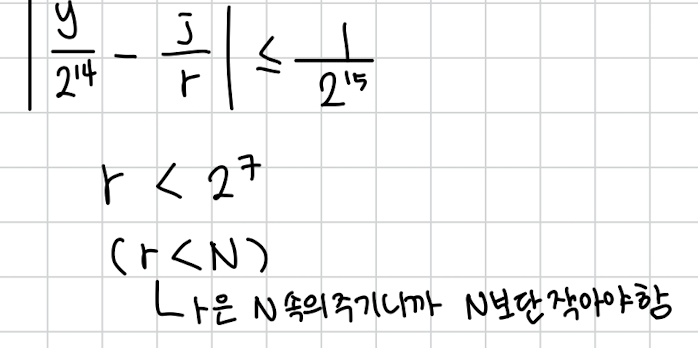
$r$은 $N$보다 작아야하니까 $2^7$보단 작아야 하고 처음에 세웠던 부등호도 만족하면 그건 우리가 찾던 $\frac{j}{r}$ 일 것입니다 .

한번 부분합을 구해보면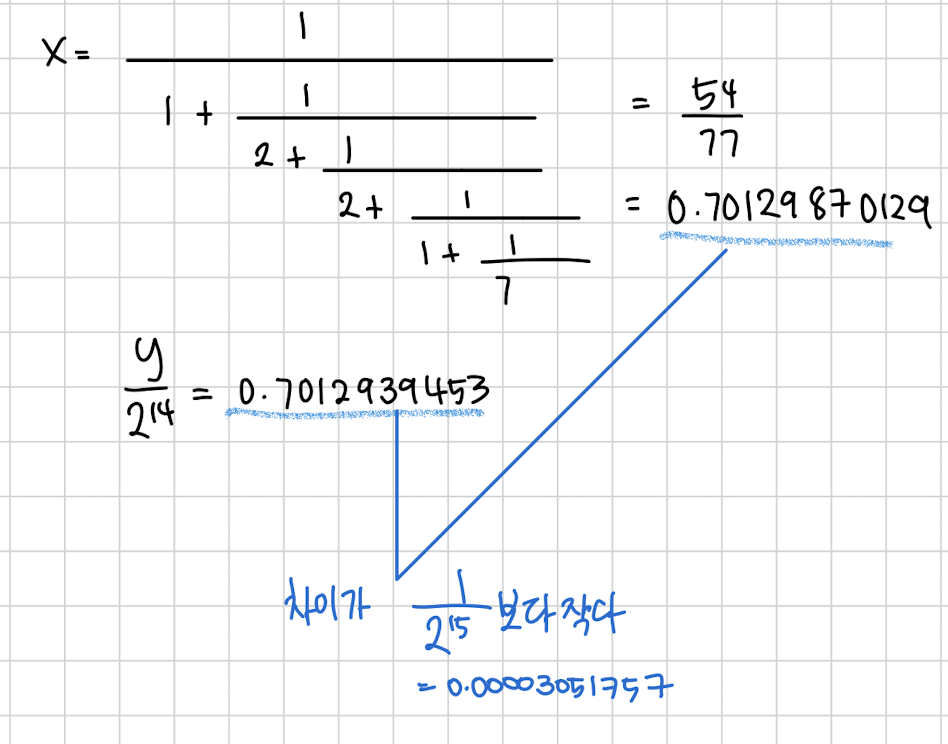
조건을 만족하는걸 확인할 수 있고
$\frac{j}{r}$ 은 $\frac{54}{77}$ 인걸 알 수 있습니다. 근데 주의해야하는게 분수라서 약분된 값일 수도 있습니다. 그러니까 r은 77의 배수인거죠. 근데 77의 배수중 128보다 작은건 77밖에 없으니 r은 77입니다.

이제 이걸로 어떻게 Factoring하는지 알아봅시다.

소수를 찾는 과정은 운에 맡기는 부분이 있긴하다.
어쨌든 이 주기를 찾는 Shors 알고리즘을 통해 r을 찾고 그거를 반절로 나누고 -1 +1 을 각각해주면 그게 N의 약수를 가지고 있는 애들이다.