No cloning Theorem

No cloning Theorem

it is impossible to create an independent and identical copy of an arbitrary unknown quantum state.

No cloning Theorem은 임의의 퀀텀 상태를 복제할 수 없다는 뜻입니다.
예를 들어 지금 컴퓨터에는 ctrl+c , ctrl+v 로 손쉽게 복사 붙여넣기를 할 수 있습니다. 그냥 01010110 이란 데이터가 있다면 그냥 복사해서 다른 곳에 저장할 수 있죠. 그런데 퀀텀에선 이런게 안된다는 이론입니다.

증명은 생각보다 짧아요.

임의의 상태를 복제할 수 없다 . 라는 것을 다른 말로 하면

어떤 임의의 상태를 복제하는 Unitary operation U가 존재하지 않는다.

라고 할 수 있습니다.

서로 다른 두 상태 $|\psi\rangle , |\phi\rangle$ 를 복제하는 U가 존재하지 않는다는 소리입니다. 여기서 $|0\rangle$은 빈 저장소라고 생각하면 됩니다. register같은 역할을 하는 ...
그래서 주어진 임의의 상태를 0에 그대로 붙여넣을 수 있는 이런 U가 존재하지 않는다라는게 주장입니다.

증명은 이제 이런 두 임의의 상태를 복제할 수 있는 U가 존재한다고 가정을 합니다.
그리고 그게 이게 말이 안된다 라는걸 보여줌으로써 U가 없다는 것을 증명합니다.

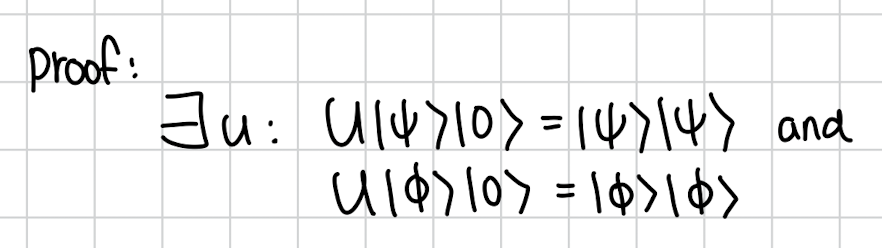
임의의 두 상태를 복제하는 U가 존재한다고 가정합니다.
우리는 그럼 각 결과 상태인 $|\psi\rangle|\psi\rangle , |\phi\rangle|\phi\rangle$ 을 서로 내적해보려고 합니다.
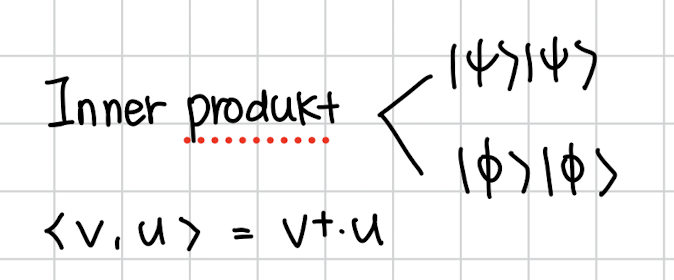내적은 그냥
$\langle v, u \rangle = v^\dagger u$
앞에 상태를 dagger operation취하고 서로 곱하면 됩니다.

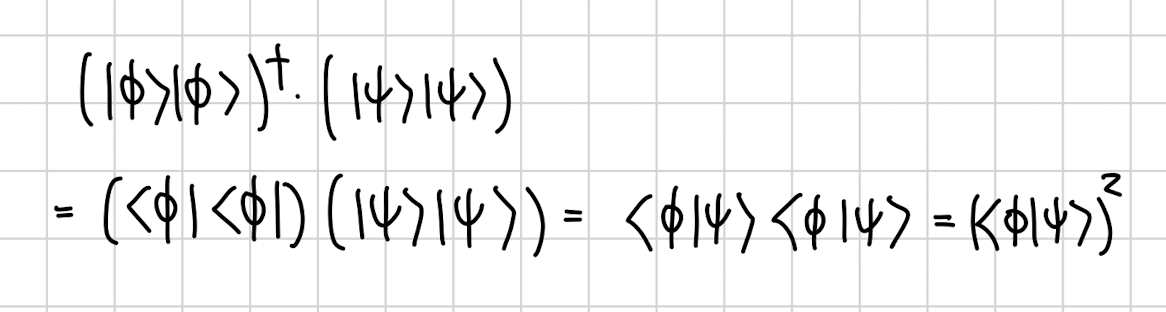
두 상태를 내적하게 되면 다음과 같이
$(\langle \phi|\psi\rangle)^2$ 가 됩니다.

근데 우리는 다음과 같은 U가 존재한다고 가정했기 때문에
$U|\psi\rangle|0\rangle = |\psi\rangle|\psi\rangle$
$U|\phi\rangle|0\rangle = |\phi\rangle|\phi\rangle$
내적을 다음과 같이도 표현할 수 있습니다.

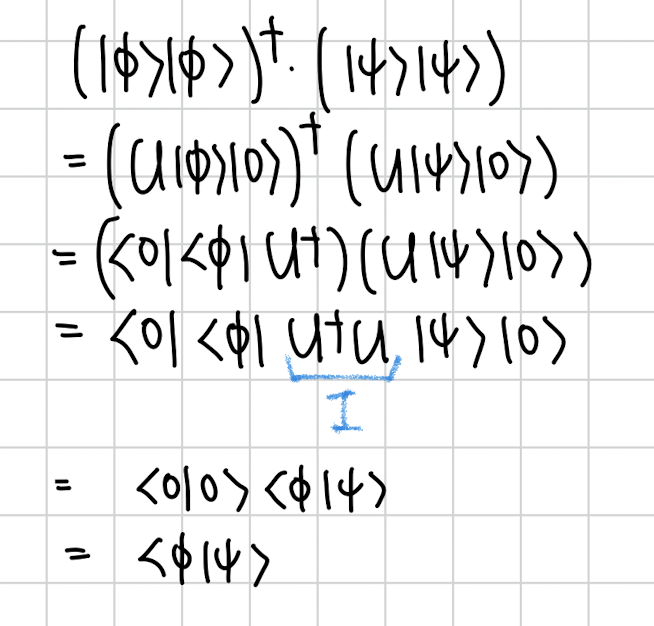
여기서 내적은 $\langle \phi|\psi\rangle$ 라고 나옵니다 .

그럼 유니터리는 내적을 변화시키지 않기때문에
첫번째 결과 $(\langle \phi|\psi\rangle)^2$ 와 두번째 결과$\langle \phi|\psi\rangle$가 같아야 합니다.

그러기 위해서는 내적값인 $\langle \phi|\psi\rangle$ 가
1이거나 0이거나 둘 중 하나여야 합니다.

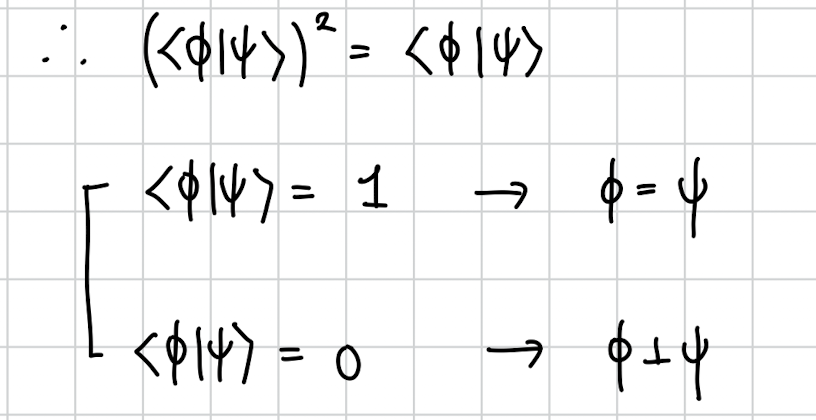
그 경우는 서로 상태가 같거나 , 서로 직교하거나 두 경우입니다.
서로 상태가 같은 경우란건 그냥 항상 그 상태만 두개 출력하는 일을 하는 유니터리 인거고..
상태가 서로 직교할때 복제 할 수 있다는건 그냥 클래식 컴퓨터가 하는 일입니다. 퀀텀 상태에서 직교하는 두 상태 0 과 1은 클래식 컴퓨터에서 0과 1에 해당하기 때문에 이런 경우는 양자 상태를 복제한다기보다 고전 정보를 복제하는 셈이라고 볼 수 있습니다.

서로 다른 일반적인 양자 상태는 이 두 조건을 만족하지 않기 때문에,
그 어떤 유니터리 연산도 모든 상태를 복제할 수 없게 됩니다.

공부한거 정리한거라 설명이 틀릴 수도 있어요..