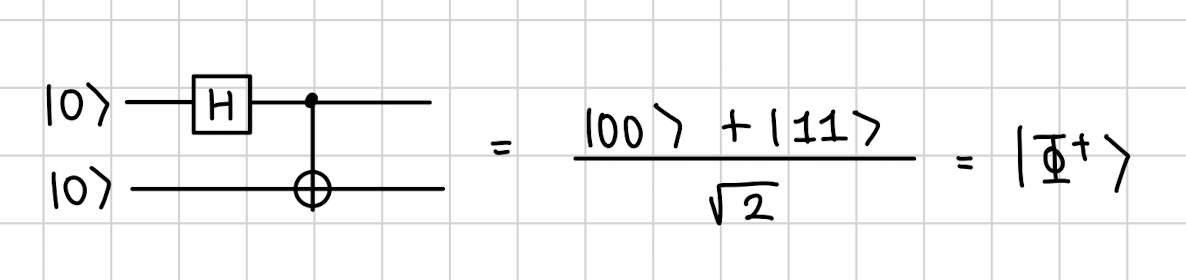Quantum Teleportation

Quantum Teleportation

1. Alice와 Bob은 예전에 만났지만 지금은 떨어져 살고있다.
2. 옛날에 같이 Bell state 를 만들고 첫번째 비트는 Alice가 두번째 비트는 Bob이 나눠 가졌다.
3. Alice는 Bob에게 임의의 퀀텀 상태를 전송하고 싶다.
4. 하지만 Bob이 어디에 있는지 알 수 없다.
5. Alice는 Bob에게 Classical 데이터만 전송할 수 있다.

Bell state

위와 같은 서로 얽혀있는 상태를 Bell state라고 합니다.
두가지 상태 $|00\rangle,|11\rangle$가 동일한 확률로 존재하는 상태로
만약 한 큐빗을 측정했는데 0이 나왔다면 두번째 큐빗도 0이되고
만약 1이 나왔다면 나머지 두번째도 자동으로 1로 확정됩니다.
왜냐면 $|00\rangle$ 또는 $|11\rangle$ 만 가능하니까!

이렇게 얽혀있는 상태를 Bell state라고 하고
Alice랑 Bob은 이런 얽혀있는 상태를 각자 한 큐빗씩 가지고 갑니다.
그리고 Alice가 멀리 떨어진 Bob에게 임의의 어떤 quantum state를 전송하고 싶은데 오직 classical data만 전송 가능합니다.

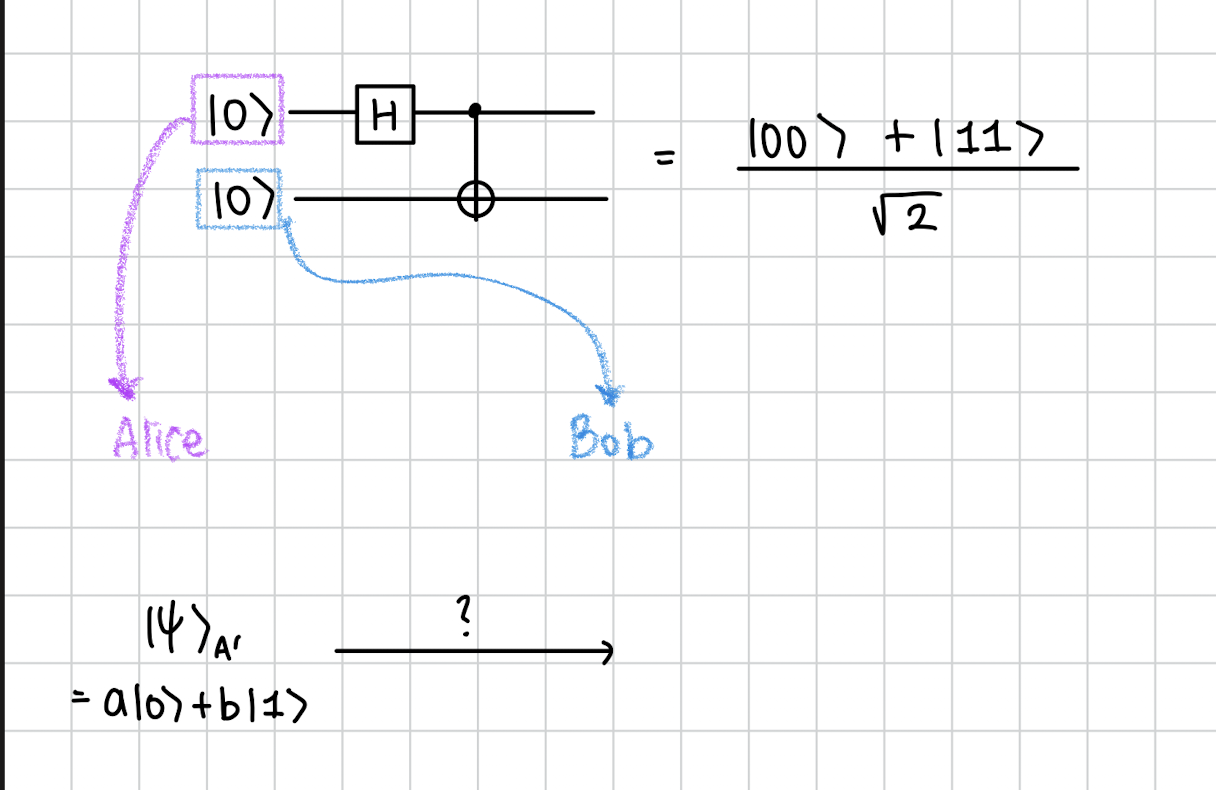
여기서 Bob에게 이 어떤 임의의 상태 $|\psi\rangle = a|0\rangle+b|1\rangle$를 전달하는 방법이 이 teleportation입니다.

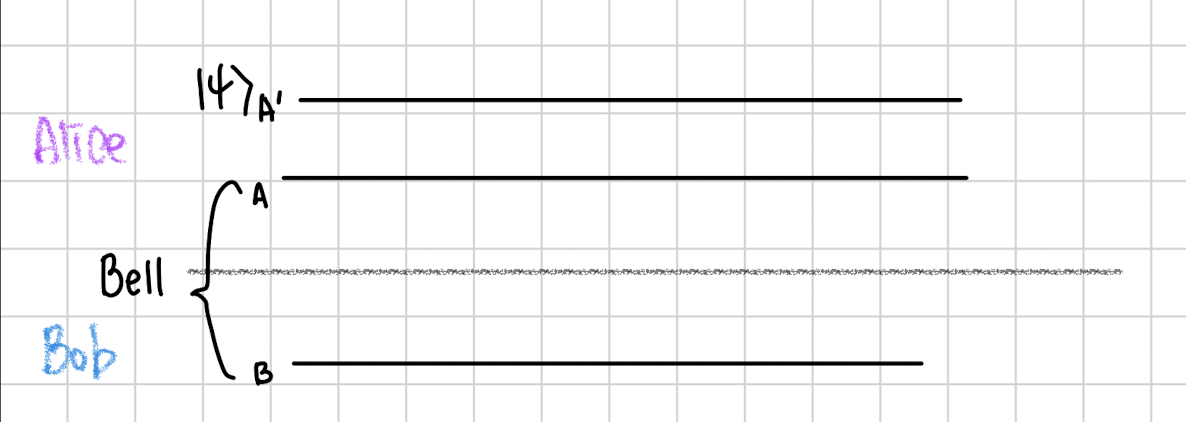
이게 초기 상태입니다. A와 B는 얽혀있는 Bell state의 두 큐빗을 나타내고
A´은 Alice가 보내고 싶은 임의의 상태입니다.

이걸 수식으로 하면 다음과 같습니다.

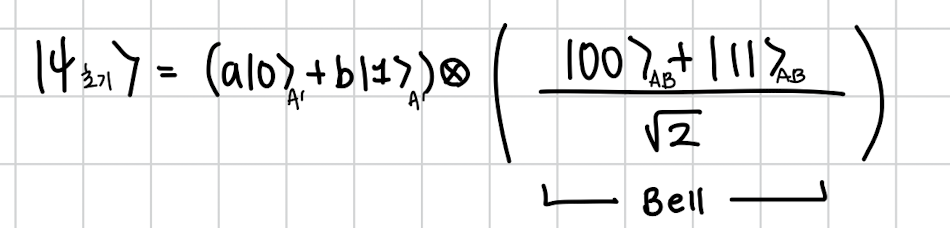
이제 다음이 Quantum teleportation 전체 회로입니다.

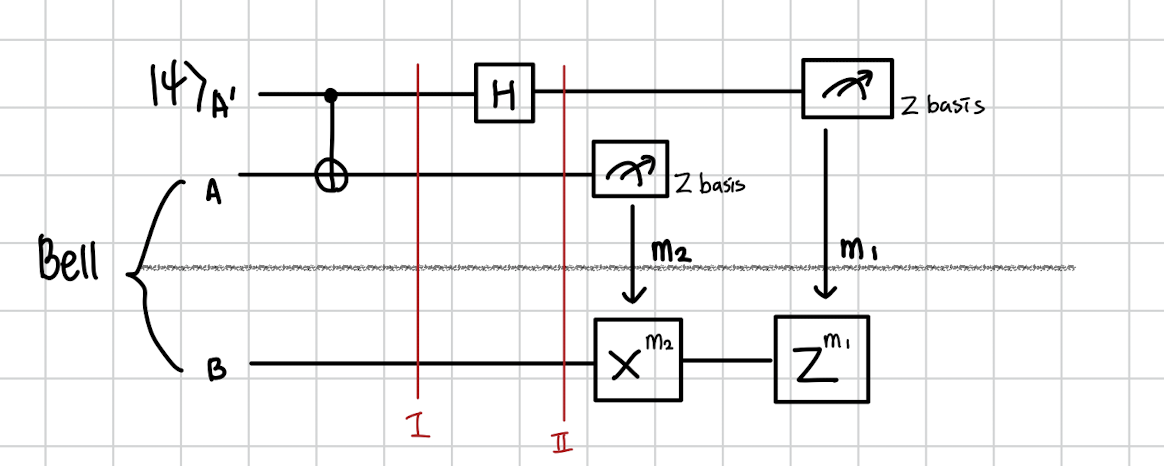
CNOT과 H를 통과하고 A´과 A를 측정하고 그 결과인 m1 과 m2를 Bob에게 전달합니다. 이 결과는 0또는 1입니다. 그래서 m1 m2는 00 01 10 11 이 4가지중 하나가 됩니다. 클래시컬 데이터여서 그냥 밥에게 그 결과를 전달하면 됩니다.

밥은 만약 m1 m2가 0 1이라면 , X 게이트를 한번 걸어주면되고 Z는 안해도 됩니다.

만약 m1 m2가 1 1 이면 , X를 걸어주고 그 다음 Z를 한번 해주면 됩니다. m2는 X 를 m1은 Z를 담당합니다.

이러면 B가 우리가 원하던 임의의 상태인 $|\psi\rangle = a|0\rangle+b|1\rangle$ 로 변신하게 됩니다. 그러면 teleportation은 끝나게 됩니다.

어떻게 가능한지 단계별로

자세히 보면,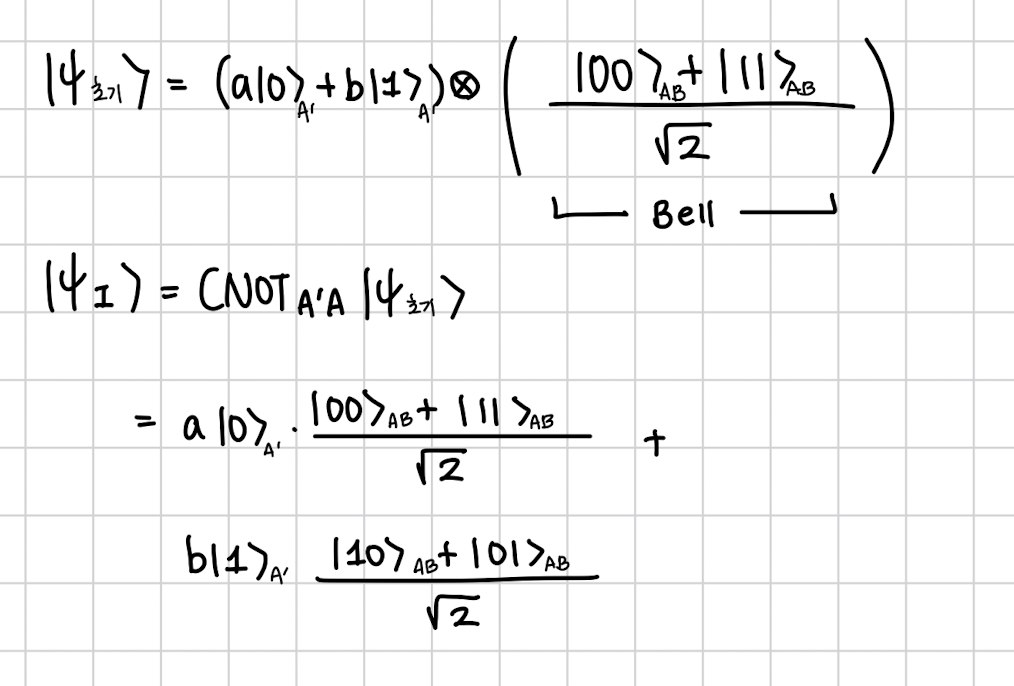
CNOT 적용후 결과. A´이 0일때는 A가 변하지 않고 , A´가 1일때는 A가 0에서 1로 , 1에서 0으로 flip됩니다.

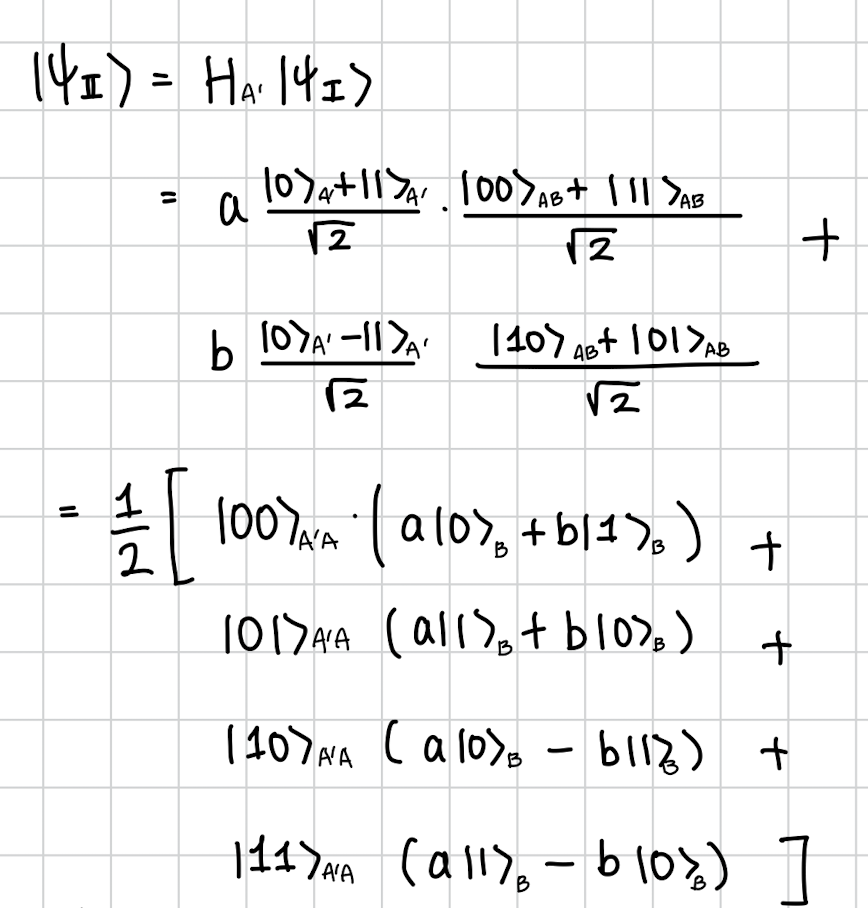
Hadamard 적용 후 결과.

결과를 정리해보면

각각 A´A 결과에 따라 B가 결과 상태에서 살짝식 달라진다는걸 알수있습니다.

예를 들어 m1 m2 가 0 1 이라면 B는 $a|1\rangle+b|0\rangle$인데 이는 X게이트만 취해서 0과 1을 바꿔주면 금방 우리가 원하던 $a|0\rangle+b|1\rangle$로 바뀌게 됩니다.

그래서 Bob은 Alice에게 m1 m2 측정 정보를 전달 받고 그 결과에 따라
X와 Z를 각각 적용할지 말지 정합니다.

1 1이면 둘다 적용하고 0 1 이면 X만 1 0 이면 Z만 0 0 이면 그대로 두면 됩니다.

이런 특성을 이용해서 4가지 경우 모두 다 B를 성공적으로 원하던 상태로 바꾸는게 가능해졌습니다!

그리고 각각의 경우는 모두 동일한 $\frac{1}{4}$ 확률을 가집니다.

이 teleportation은 m1 m2를 전달하는 과정이 필요해서 즉각적인 통신이라고는 보기 어렵습니다.
그리고 no cloning theorem 과도 충돌하지 않는게 Alice가 Bob 에게 m1 m2 정보를 전달하기 위해 측정을 하면서 원래의 상태는 붕괴됩니다. 따라서 원본 큐빗을 파괴시키면서 Bob에게 전달하기 때문에 동시에 두 상태가 존재하는건 아니라서 복제라곤 볼 수 없습니다.

대학생 공부 정리한거라 틀린 설명일 수도 있어요..