마지막 velog의 글을 보니, 6달이나 쉬고 있었군요. 작년 9월부터 12월까지는 DALPA에 취직해서 ai 엔지니어로 일을 했었거든요. 1월부터 4월까지는 연구실에서 진행하는 연구에 code를 작성하는데 집중했었습니다. 성장도 성장이지만 결국 수면, 건강이 제일 중요하다는 느낌이 새삼 들더라고요.

최근에는 다시 규칙적으로 운동도 시작하고 일찍 잠을 청하는 생활을 습관화해서 깨어있는 동안에 최대한의 생산을 해내려는 노력을 하고 있습니다.

저도 이제 멸치에서 고등어로 진화중입니다. 특히, 체지방을 극단적으로 줄이려는 시도를 하고 있어요. 샐러드랑 닭가슴살의 꾸준한 섭취 및 주에 3일 이상 20~30분씩 조깅 (10 km/h)을 하기로 스스로와 약속했답니다.

가끔씩 걷다가 보면 눈을 사로잡는 대목들이 보이곤하죠. 그러고보니 최근엔 웃음이 좀 부족한가? 하는 느낌이 들기도하고요. 친구들과 있을때 자주 웃는 것 같은데 다시 Outsider의 생활로 돌아가고 있어요 ㅎ..

다시 본론으로 돌아와볼게요. 제가 1달차 석사생이 되었습니다. 주로 연구실 인턴 생활을 하면서 읽었던 논문을 velog에 정리하곤 했었지요. 요즘들어 연구의 발전속도가 더뎌서 답답함을 호소하고 있긴 합니다만...

급할수록 돌아가라!

라는 말이 있지 않습니까? 그래서 다시 바쁜 마음을 재정비하고 성능향상을 위해 차근차근 조사를 하고 있던 중입니다. transformer 모델을 활용하는데 train 속도가 빠를수록 더 많은 실험을 할 수 있기 때문에 flash attention에 관심을 안가질 수 없더라고요.

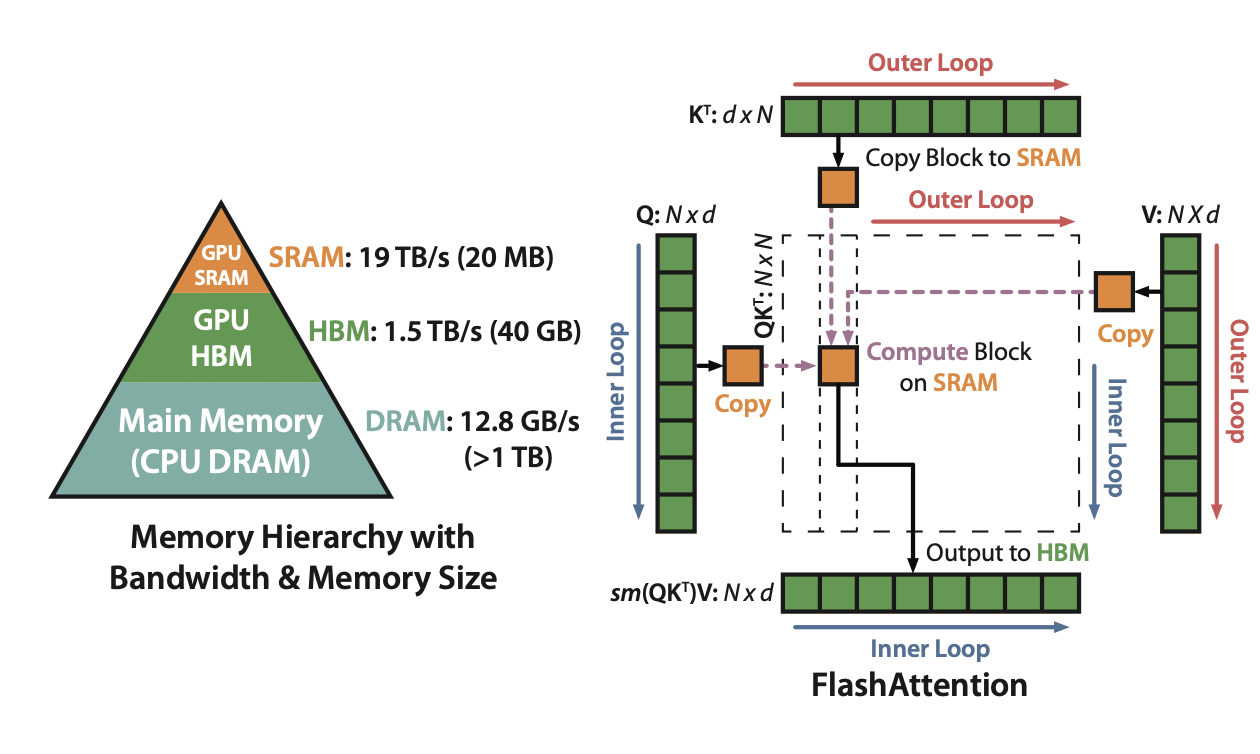
간단하게 설명하자면, original transformer의 attention 계산에 memory-access에 관련된 비효율이 존재한다는 것입니다. 이를 해결하고자 pytorch 보다 훨씬 아랫단계에서의 코드 라인을 수정하여 flash attention이라는 계산 기법을 탄생시켰습니다. Flash 어텐션은 기존의 어텐션 계산을 전혀 해치지 않으며 메모리와 속도면에서 압도적으로 훌륭하다는 특징이 있습니다. 이해하기 쉽게 허깅페이스에서 다이어그램을 제공했습니다.

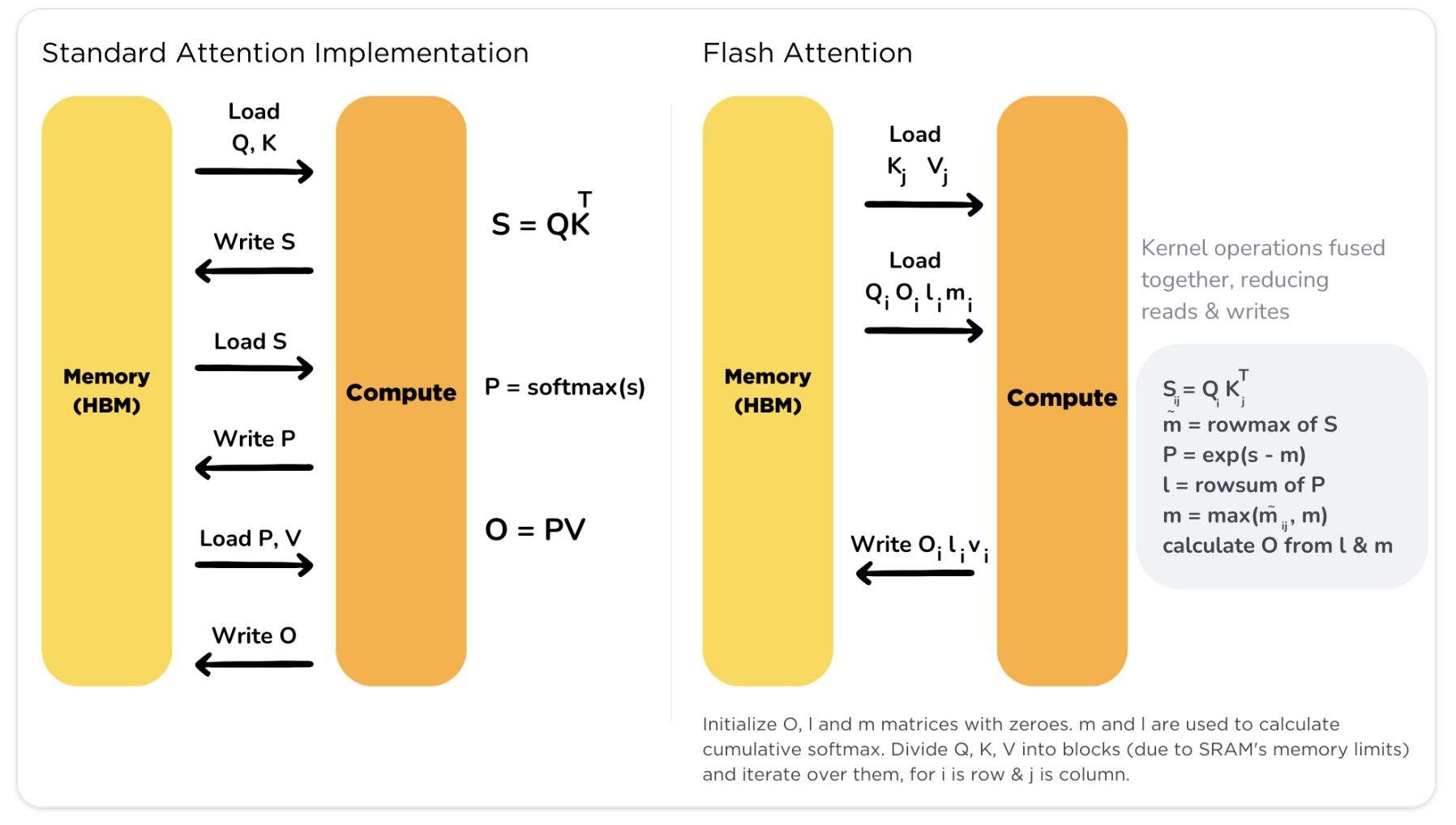
GPU에서 연산 할 때, HBM(GPU의 메인메모리)으로의 접근이 너무 많아 IO communication이 bottle-neck이 되고 있었습니다. 이를 해소하고자 Load / Write process를 압도적으로 줄였고 SRAM(GPU의 register격 cache)에서 한번에 computation을 진행하였습니다. 이를 hardware-aware programming 이라고하죠? software engineer도 hardware의 특징을 알지 못하면 비효율적인 코드를 작성하게 되므로 늘 주의를 기울여야겠다는 깨달음을 다시 한 번 느끼게 됐지요.

FlashAttention: Fast and Memory-Efficient Exact Attention
with IO-Awareness

리뷰 시작하겠습니다! (review에는 block sparse attention에 관련된 내용을 배제하였습니다.)

1. Standard attention의 문제점

standard attention은 위의 수식과 같이 query와 key의 interaction인 attention map (P)을 계산하여 일종의 pairwise coefficient를 계산을 합니다. 그 뒤, value와의 곱을 통해 해당 레이어에서 잔차에 연관된 값 (O, 추후 FFN를 통과하면서 공간변환이 한번 더 됨.)을 구할 수 있는 것이지요.

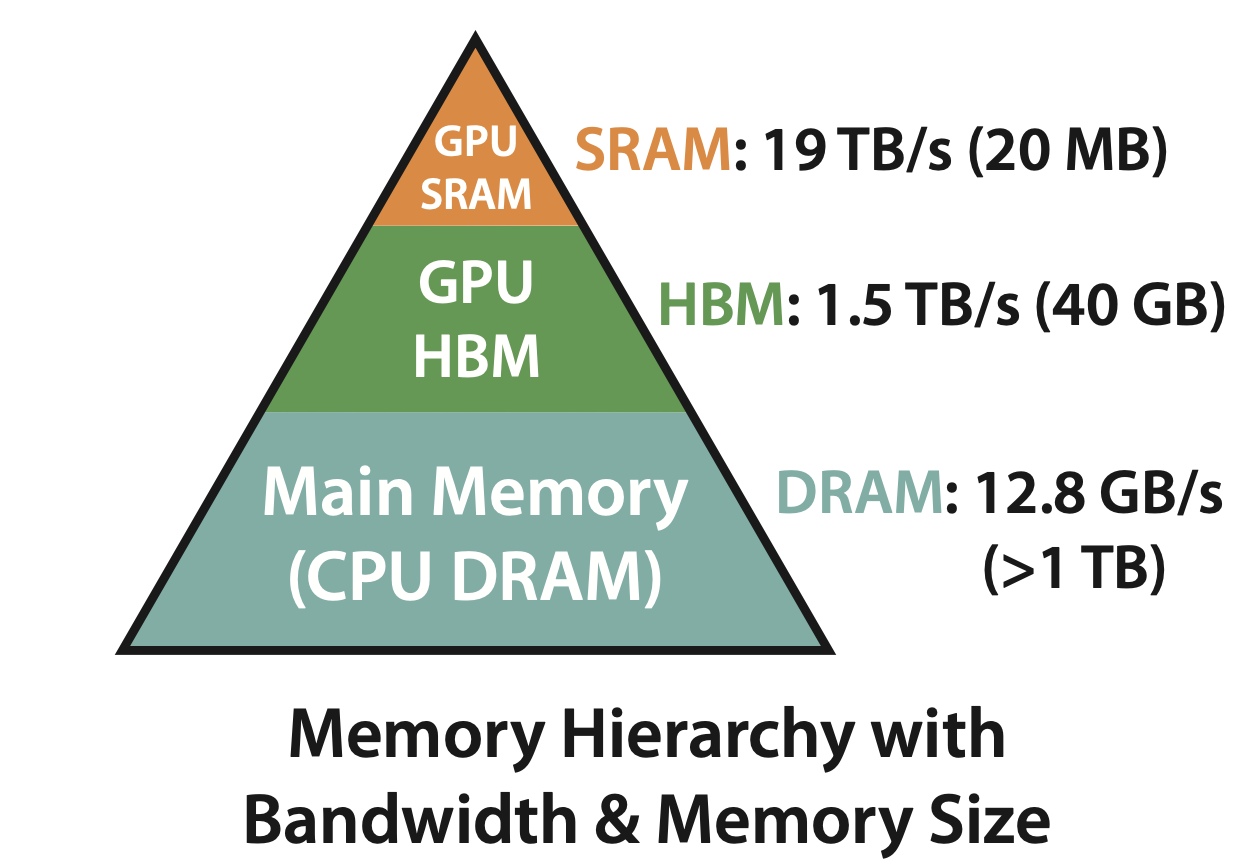
CPU와 GPU의 버스 통신 흐름에 따라 계층적으로 메모리 구조를 나타내면 위와 같습니다. CPU의 Main memory에 적재된 값이 GPU의 HBM과 GPU의 SRAM을 차례로 거쳐 적재되었을때 비로서 연산(computation)이 진행됩니다. (GPU SRAM을 마치 cpu의 L1 cache 쯤으로 생각해볼 수 있으려나요?) NVIDIA-A100의 40GB/80GB 메모리는 HBM에 해당하는 것이죠. 실제 연산은 그보다 훨씬 작은 (KB, MB 단위의) SRAM에서 진행되는 것 입니다. 따라서 CPU <=> GPU access time 뿐만아니라 GPU HBM <=> GPU SRAM의 access time 역시 관건이라고 할 수 있습니다.

간단하게 forward algorithm (설명을 위해 dropout, masking 등이 생략됨)만 살펴보겠습니다. 추후, backpropagation을 위해서 S, P, O 등을 HBM에 저장하는 것을 알 수 있습니다. S와 P 모두 (N, N) matrix이므로 N의 2차식에 비례하는 메모리 복잡도를 가짐을 알 수 있죠. 이는 flash attention을 통해 N의 1차식에 비례하는 메모리 복잡도로 개선됩니다.

2. Attention의 잘게 쪼개서 생각하기

Q, K, V를 쪼개어 block 단위로 HBM에서 관리하고 SRAM에서 한번에 계산하도록 하는 것이 핵심이라고 할 수 있습니다. 특히 attention map P를 생성하기 위해 softmax 연산이 필요한데요, 이는 column 방향의 연산이므로 Q와 K를 행 방향(embedding의 dimension은 그대로 유지)으로 잘게 쪼깬 뒤 merge 하는 방식을 생각해볼 수 있습니다. 비록 sram에서의 연산시간이 소폭 늘어날지라(recomputation에 의해)도 memory end-point간의 access time이 줄어든다는 것입니다. 쪼개진 각 block이 sram에서 한번만 계산하도록 설계했기때문이죠. 이는 matrix multiply와 softmax를 연산 우선순위대로 진행하는 standard attention과 상당히 다른 부분이죠.

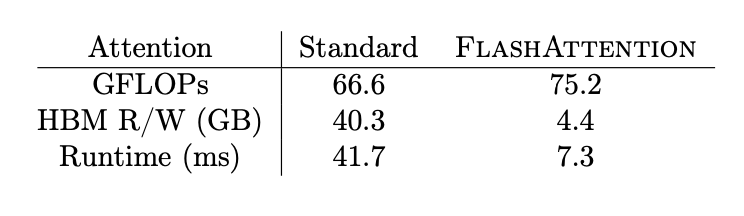
위의 실험 결과에서도 관찰할 수 있듯, recompuation으로 의한 중복계산으로 GFLOPs는 소폭 상승했지만 HBM의 access memory가 압도적으로 줄어들어 runtime에서 5배 이상의 상승을 확인할 수 있습니다.

위의 내용을 직접 구현하기 위해서 본 논문에서는 tiling과 recomputation이라는 method를 제안합니다.

titling

아래와 같이 softmax 는 vector의 maximum value를 중심으로 rescaling 하여 계산해도 같은 값이 나오는 것을 확인할 수 있습니다. 이때, 새롭게 등장한 variable m과 l에 주목해봅시다. m은 block x의 maximum value이며 l은 softmax(x)를 normalize하기 위한 summation value입니다.

아래와 같이 blocks의 l과 m을 활용해 concatenation 했을때의 softmax value를 계산할 수 있습니다. l과 m을 softmax normalization statistics라고 부르더군요.

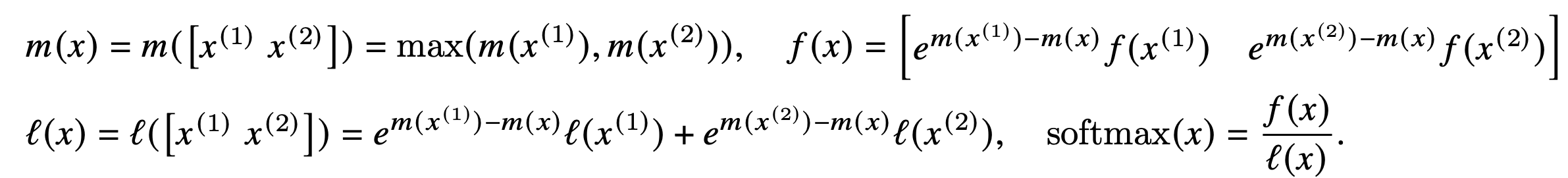
이는 곧 attention map (P)를 굳이 HBM에 저장하지 않고도 forward, backward process를 진행할 수 있음을 시사합니다.

recomputation

backward process에서 Q,K,V에 대한 gradient descent를 진행해야되므로 S,P의 값이 필요합니다. 한편, O와 (𝑚,l)만을 활용해서 S와 P를 쉽게 복원할 수 있습니다. 이는 gradient checkpointing이라는 기술과 견줘서 생각해볼 수 있습니다. 이들은 memory와 speed가 trade off 관계에 놓여있는 것에 반해 Flash attention은 HBM accesses가 현저히 줄어들기 때문에 speed up이 발생합니다.

3. Flash Attention

Flash attention 알고리즘을 정리하면 위와 같습니다. 위의 알고리즘과 연동되는 그림도 제시해서 이해하기 수월했습니다. on-chip이라고 표기된 부분이 sram에서 계산을 진행하는 부분이고 write을 하는 line이 HBM에 access하는 것임을 알 수 있습니다. 각 블락이 커져감(오른쪽으로 커짐)에 따라 l과 m을 업데이트 해주고 이를 활용해 O([N, d] 차원)의 row vector에 정합성에 맞게 summation 해주어 O를 획득하는 것을 확인할 수 있습니다.

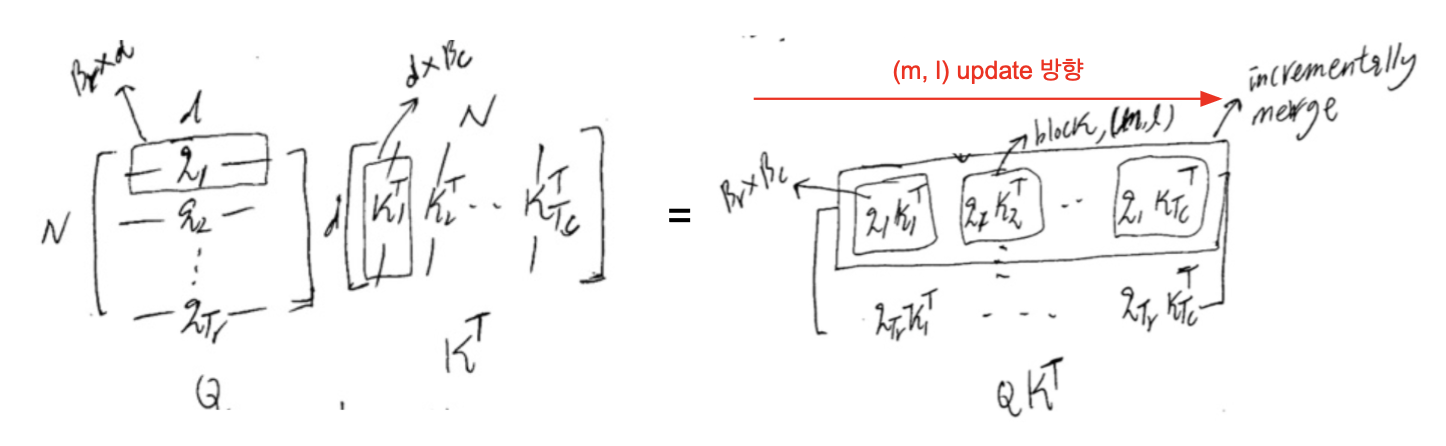
softmax of multiply(Q, transpose of K)의 관점에서만 생각해보면 위의 그림과 같습니다. Q, K를 각각 $T_r, T_c$ 개의 block으로 쪼개면 왼쪽의 그림처럼 생각해볼 수 있죠. 이를 [$T_r, T_c$] 의 blocks를 titling 해서 softmax normalization statistics를 업데이트해주면 결국 전체 S에 대한 정보를 획득할 수 있게됩니다.

P, S 등이 직접적으로 HBM에 write되지 않다보니 long sequence에 대해서 큰 효율(sub-quadratic algorithm)이 있을것으로 예상됩니다.

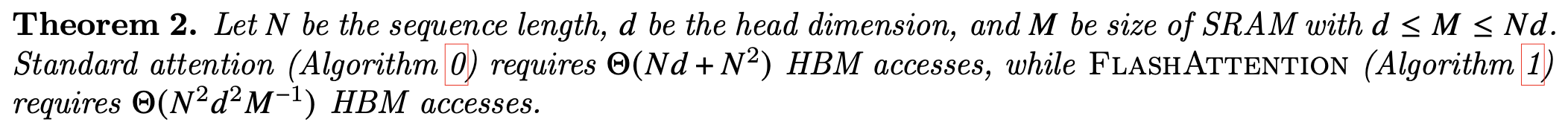
이론적으로 복잡도를 분석했을때, HBM의 접근의 측면에서 위와 같은 차이가 발생합니다. $M = \theta(Nd)$ 임을 감안하면 FlashAttention의 경우에 N의 1차식에 비례하는 HBM access 알고리즘임을 확인할 수 있죠.

4. 실험 결과

실험 결과는 간단하게 두가지만 가져와봤습니다.

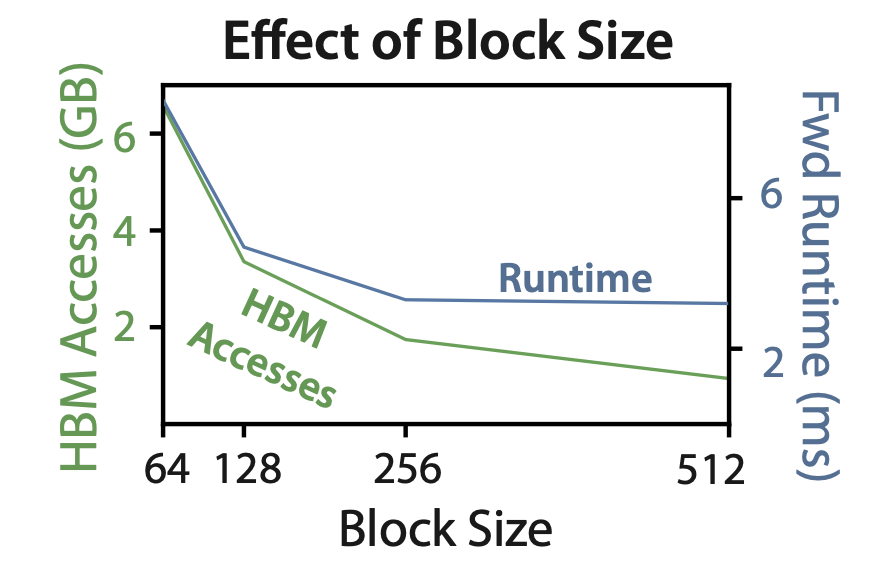
SRAM의 block size (앞서 논의했던 block과 동일합니다.)에 따라서 HBM access 횟수와 runtime의 관계를 나타낸 것 입니다. 256차원 이후로는 runtime이 포화되는 것을 확인할 수 있습니다.

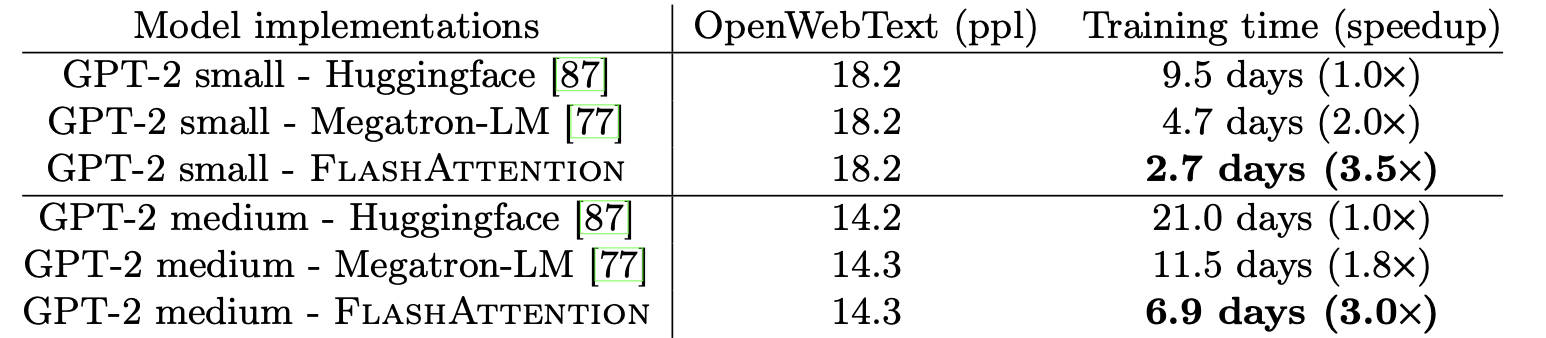
GPT-2의 훈련 시간이 얼마나 빨라지는지에 대한 실험도 소개했습니다. 본래의 transformer보다 약 3배이상 빨라지는 결과를 확인해볼 수 있었습니다.

마치며...

transformer의 표준 구현이 flash attention을 반영해줬으면 좋겠습니다. 누군가가 annotated tranformer: revision with flash attention과 같은 reference notebook code를 제작해놓으면 github star 많이 받을 것 같네요. 암튼, 이를 연구에 어서 적용해서 결과값을 해치지 않지만 속도면에선 상당한 이득을 볼 수 있는 flash attention을 임베딩해놓도록 하겠습니다.

다음편은 neural combinatorial optimization 혹은 diffusion 중 하나의 논문으로 리뷰해보겠습니다. 이상입니다.