요즘 근황

오랜만에 velog로 돌아왔습니다. 1학기가 종강한 뒤, 승근, 성영이와 함께 diffusion 스터디를 꾸려서 저널 클럽과 유사한 느낌으로 매주 대면 meet-up하고 있습니다. 논문은 주당 3개씩 선정을 하고 있고요, 모두가 논문을 읽되 각 논문 당 한명씩 전담 마크하여 디테일한 지식을 공유하는 것이 이번 스터디의 목적이 되겠습니다. 세명의 각기 다른 견지에서 흐름을 바라볼 수 있다는 점에서 풍성하게 이야기가 되는 것 같네요.

승근맨의 발표 중 캡쳐해봤습니다.

별개로, 외주 작업이 많진 않았지만 모두 stable diffusion 관련한 것이었습니다. 공교롭게도 연구, 외주, 스터디가 물아일체로 diffusion을 향해가고 있습니다.

AI project 전문가 크몽에 등록해보니 diffusion에 관련된 의뢰만 두건 받았습니다.

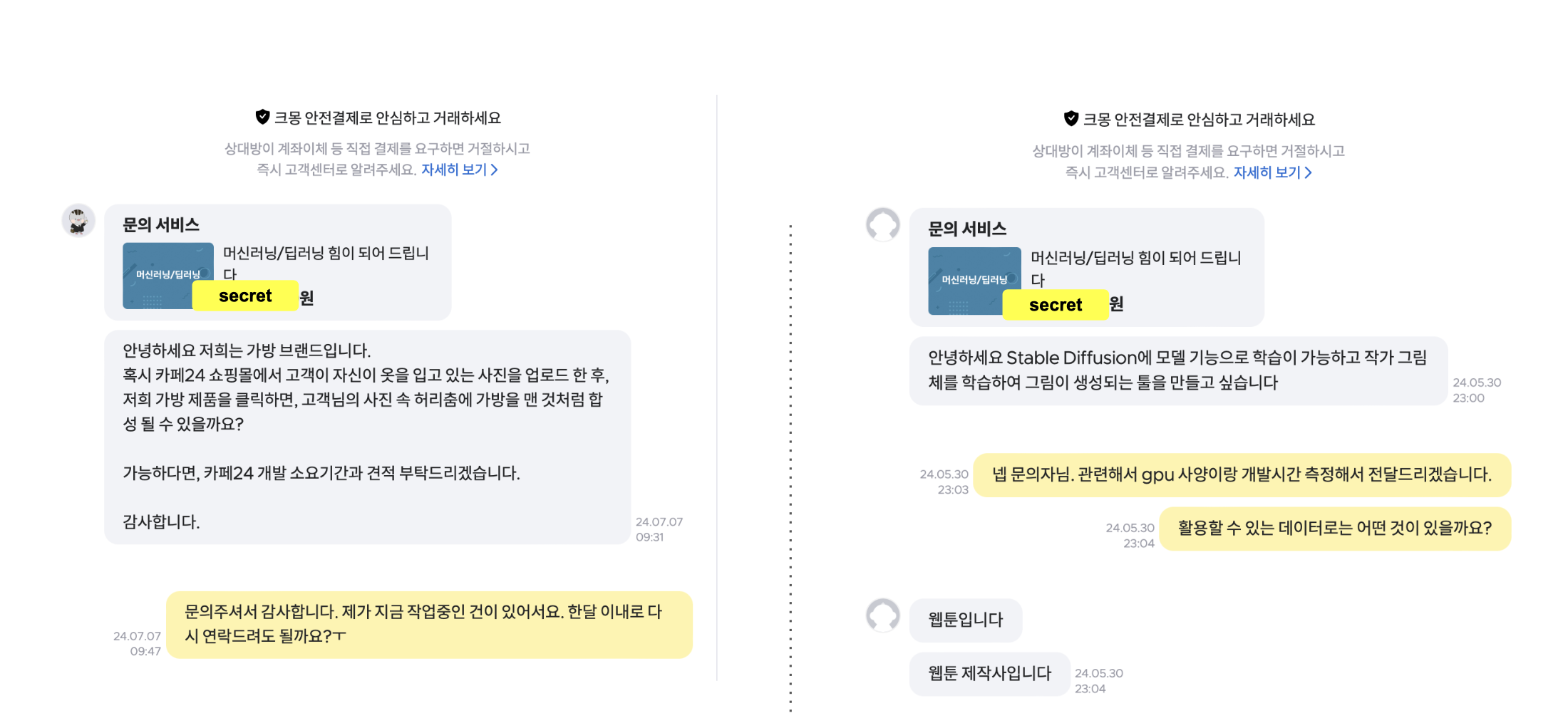
일단 콘티에서 작가의 고유의 그림체를 살리는 프로젝트를 진행하고 있습니다. (콘티, 그림체) 쌍의 데이터를 수집해서 학습을 진행하는 중 입니다. 정형화된 데이터가 아니라서 학습도 어렵기도하고 콘티, 그림체 사이에는 무수히 복잡한 관계성이 있어서 inverse problem으로 취급하기도 어려운데요. 당장은 (그림체 canny edge, 그림체) 쌍만을 활용해서 controlnet을 훈련시킨 상태로 1차 작업을 마무리 했습니다. 이후로는 브라우니안 브릿지 혹은 슈레딩거 브릿지를 활용한 image translation task를 review하고 적용시켜봐야겠다는 목표를 세웠습니다.

Stable diffusion webUI와 Controlnet을 활용한 콘티에서 그림체로의 모델 개발

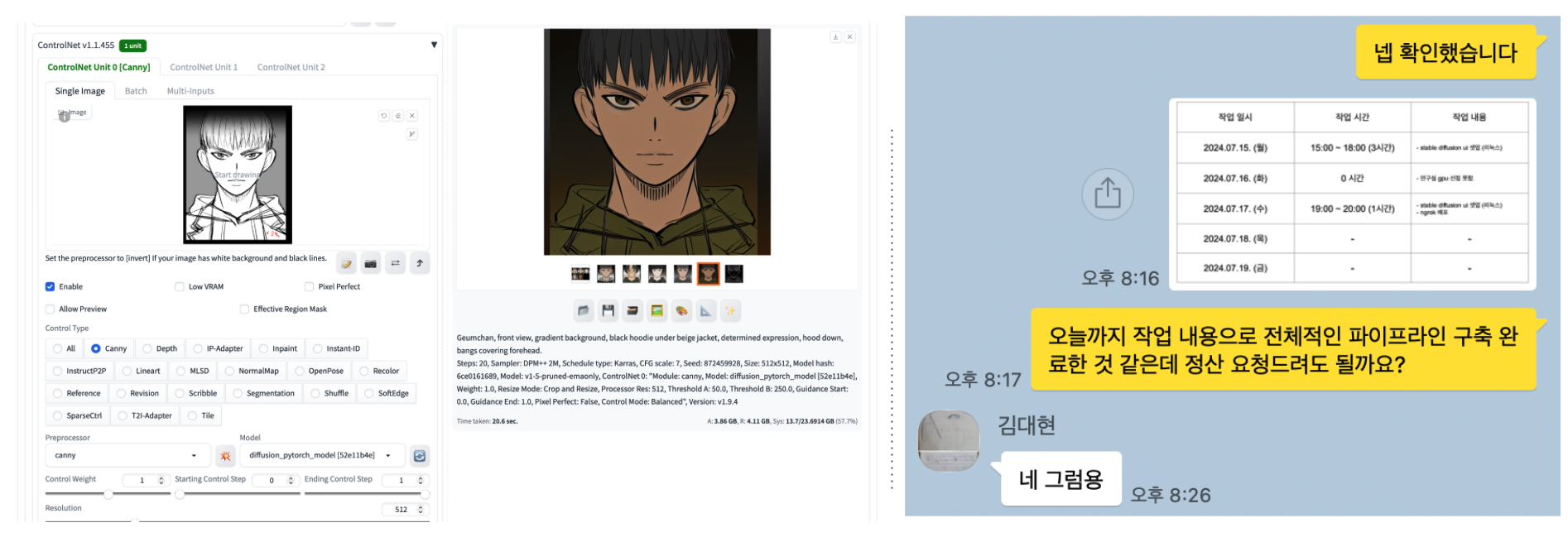
이번 기회에 inverse problem에 관련된 논문을 review하면서 콘티에서 그림체로 향하는 model이 아직 인간 지식의 경계에 머물고 있다는 생각이 들었습니다. 아무튼, 이런 난제를 어떻게든 해결하는 것 또한 공학자의 몫이니 잘 헤쳐나가 보겠습니다.

DPS 논문 링크: https://arxiv.org/abs/2209.14687

Inverse Problems?

Inverse Problem의 formulation

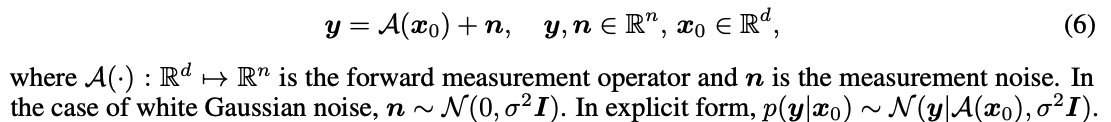
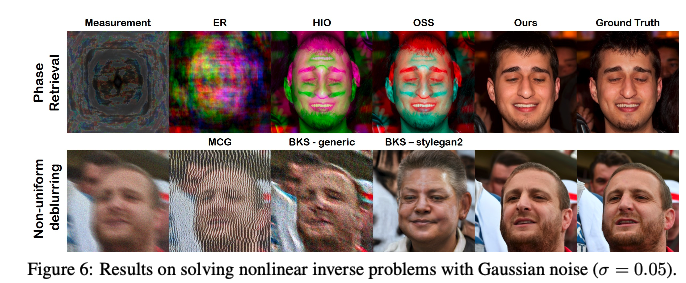
기본적으로 inverse problem은 measurement y를 관찰했을때, ${x_0}$로 복원해내는 모든 문제를 총망라합니다. 이때, 비가역 변환 A에 대해서 ${x_0}$와 y는 위와 같은 stochastic equation의 식을 만족하는데요, 직관적으로 ${x_0}$에서 y로 정보를 압축한다는 것을 알 수 있습니다. 이때, 정보의 손실을 sigma 만큼의 standard deviation을 가지는 normal distribution의 형태로 표기할 수 있습니다. 본 논문에서의 A는 inpainting, gaussian deblur, super-resolution, motion deblur 등의 linear transformation이 될 수도 있지만, Phase retrieval 혹은 non-uniform deblur과 같은 non-linear transformation 역시 함께 취급해 고려해줍니다.

Inverse problem을 풀기 위해서는 최소한 A의 formulation을 파악할 수 있어야한다.

cf.) 콘티에서 그림체로 가는 변환을 알 수 없기에 inverse problem domain에서 제시하는 solver로는 해결할 수는 없을 것 같습니다..

Linear Inverse Problem에서의 A의 예시 (Appendix B 참고)

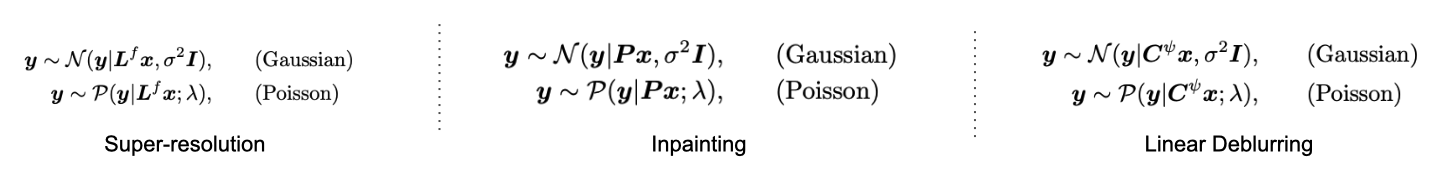
• Super-resolution: ${L^f}$ 는 bicubic downsampling block Hankel 매트릭스입니다.
• Inpainting: P는 0 혹은 1만을 원소로 가지는 마스킹 매트릭스입니다.
• Linear Deblurring: ${C^{\psi}}$는 blur kernel $\psi$에 대한 block Hankel 매트릭스입니다.

Non Linear Inverse Problem에서의 A의 예시 (Appendix B 참고)

• Non Linear Deblurring: ${F_{\phi}}$는 non linear deblurring kernel을 학습한 neural network를 나타냅니다.
• Phase Retrieval: F는 2D 이산 퓨리에 변환이며, P는 oversampling matrix 입니다.

다양한 task의 inverse problem과 DPS의 solutions

Related works & Contributions

대게의 diffusion 기반의 inverse problem은 measurement y를 먼저 측정한 이후에 prior인 P(x)를 기반으로 posterior P(x|y)의 approximation을 계산합니다. 그 뒤, posterior를 활용해 sampling을 반복적으로 수행하여 기대했던 x로 가까워지도록 denoising을 수행합니다.

한편, 본 논문에서는 두가지 방법론, Measurement subspace로 사영하면서 진행하는 접근 방식(Improving diffusion models for inverse problems using manifold constraints)과 SVD를 활용해 diffusion을 spectral domain에서 활용하는 방법(Denoising diffusion restoration models)을 주로 언급했습니다.

이들이 가진 문제점을 아래와 같이 비판했습니다.

1) Measurement에 noise가 껴있으면 제대로 문제를 풀지 못함.
2) Linear inverse problem만 해결가능.
3) SVD의 경우 계산량이 너무 많음.

그 동안의 작업들은 linear inverse problem만 다룰 수 있었지만, 본 논문에서 제시하는 DPS는 non linear inverse problem을 다룬 첫번째 논문이며 순수한 image domain에서만 데이터를 다룰 수 있다는 점에서 좋은 인상을 줍니다. 이들은 추후 Improving diffusion models for inverse problems using manifold constraints과의 연관지어 방법론의 차이점에 대해 후술합니다.

Score-based Diffusion models와 Inverse problem solving with diffusion models

Song이 제시했던 score-based generative model with stochastic differential equations

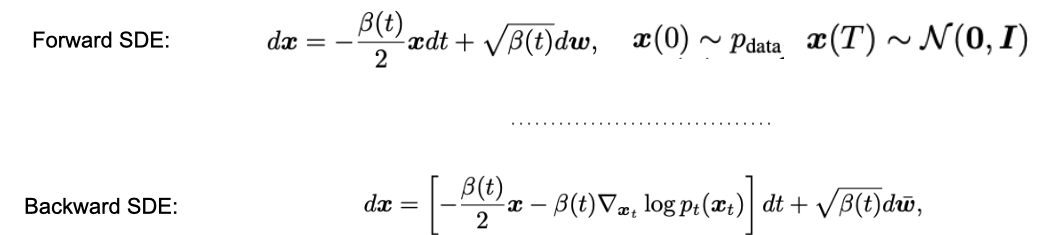
위의 식에서 알 수 있듯, continuous domain에서 정의된 time이 흘러감에 따라 forward differential stochastic equation data (${x(0)}$)가 점점 corruption이 진행되어 random noise(${x(T)}$)로 향하는 것을 확인할 수 있습니다. 한편, random noise에서 다시 data로 복원하기 위해서 backward SDE의 흐름을 따라가면 됩니다. 이를 위해 transition probability의 미분 값이 필요한 것을 확인할 수 있지요. 이를 approximate하기 위해 딥뉴럴 네트워크 기반의 score function이 도입되었고 아래와 같이 샘플링을 활용해 학습을 진행할 수 있습니다.

score-based generative model with SDE의 loss designs

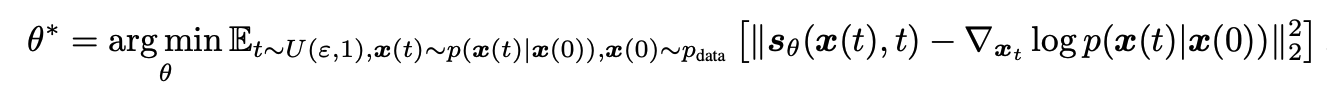
Diffusion 모델을 활용해서 inverse problem을 풀기 위해선, 위의 score function 대신 posterior를 활용해 control 해야 됩니다. Baseyian rule에 의해 아래의 식을 만족하므로:

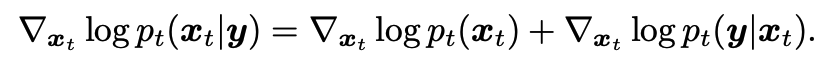
아래의 reverse sampling의 식을 고려할 수 있습니다.

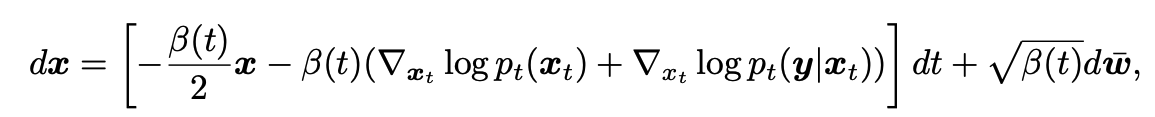
첫번째 term은 pretrained된 diffusion 모델에서 확인할 수 있는 prior이므로 손쉽게 얻을 수 있습니다만, 두번째 likelihood term은 intractable 하기때문에 적절한 approximation이 필요합니다. 이를 디자인 한 것이 본 논문의 핵심임을 알 수 있지요.

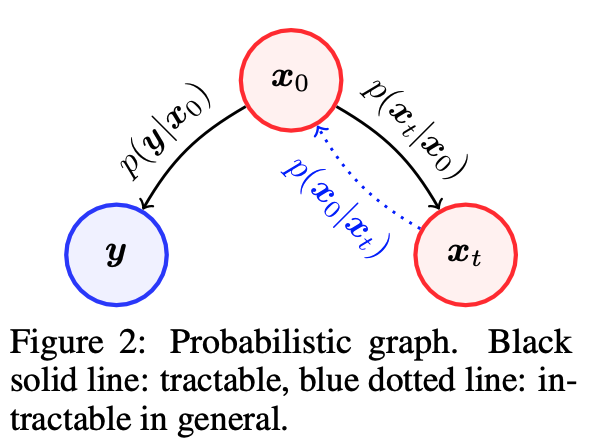
위의 확률 그래프에서도 확인할 수 있듯, $x_0$와 $y$는 forward measurement operator 디자인에 의해 관계성을 가지고, $x_0$와 $x_t$는 transition kernel에 의해 관계성을 가지지만 $x_t$와 $y$의 직접적인 관계가 없다는 것(intractable)을 확인할 수 있지요.

Diffusion Posterior Sampling (approximation of the likelihood)

Expectation of x_0 given x_t tweedie의 formula에 의해 위와 같이 conditional expectation을 계산할 수 있습니다. $x_t$와 $y$의 관계를 만들어 내기 위해 $\hat{x}_0$를 경유하는 느낌이 사뭇 드네요. 물론 posterior mean은 아래와 같이 approximate하여 사용할 예정입니다.

Expectation of x_0 given x_t with score function

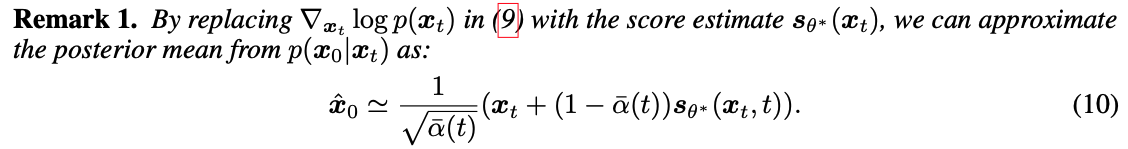
대망의 하이라이트

위와 같이 jenson gap을 정의하면 두 transition probability $P[ y|\hat{x}_0]$와 $P[y|x_t]$가 sigma의 역제곱에 비례하는 upperbound가 잡힌다는 것을 알 수 있습니다. 따라서, sigma가 무한대로 발산할 때 (y의 복잡도가 충분할 때), $P[y|x_t]$을 $P[y|\hat{x}_0]$으로 근사할 수 있다는 합리적인 결론에 다다를수 있죠.

intractable => tractable, hat_x_0는 x_t에 대한 함수이므로 미분 가능

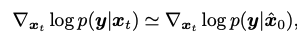
Model dependent likelihood of the measurement

$P[y|x_0]$을 Gaussian noise 혹은 Poisson noise로 고려해서 DPS 알고리즘을 완성할 수 있습니다. 대표적으로 gaussian의 경우만 살펴보도록 하겠습니다.

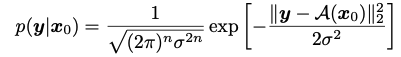
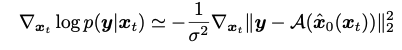
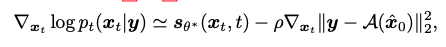
앞의 섹션에서 다뤘던 approximation of the likelihood를 십분 활용해서 likelihood의 미분값을 tractable하게 치환한 뒤, bayesian rule를 활용해 posterior의 미분값도 추론할 수 있다는 것을 나타낸 것 입니다.

Gaussian, Poisson noise에 대한 DPS 알고리즘

• 3번 라인: i번째 time step까지 고려된 noised input $x_i$를 활용해 score function을 구함.
• 4번 라인: score function을 활용해 x_0의 예측값을 구함.
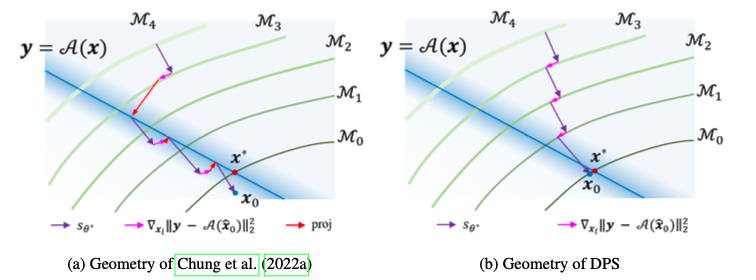
• 5, 6번 라인: pretrained 되어있는 ddpm ancestral sampling. (아래 그림의 data manifold를 이동시킴.)
• 7번 라인: posterior의 값이 증가하는 방향으로 data를 backpropagation 시킴. (아래 그림의
  data manifold 내에서 이동함.)

DPS 알고리즘의 시각화

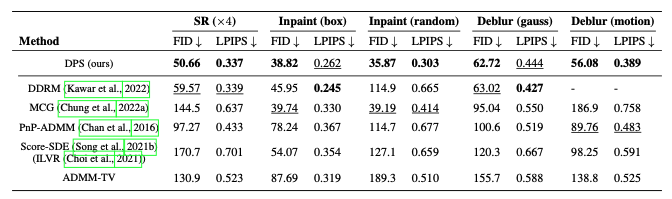
Experiments

Linear problem (SOTA with great margin)

Non Linear problem

마치며..

방학땐 무언가.. 이것 저것 잘 해보겠습니다.