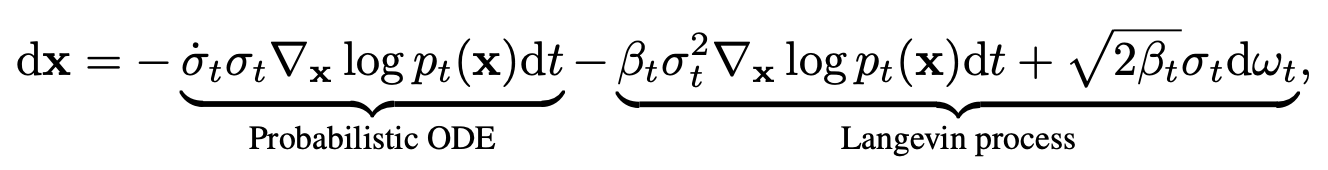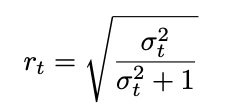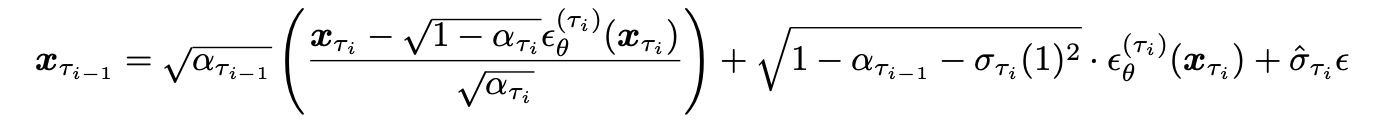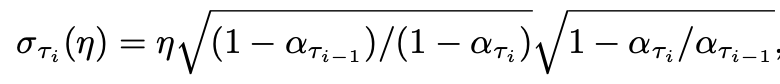PseudoInverse-guided diffusion models for Inverse Problems

Intro

Diffusion generative models을 활용해 inverse 문제를 해결하는 방식은 크게 두 가지로 나눌 수 있습니다. 하나는 각 task마다 별도의 학습이 필요한 problem-specific 방법론이고, 다른 하나는 posterior sampling을 활용한 problem-agnostic 접근법입니다. 이번에 소개해드릴 논문 "PseudoInverse-guided Diffusion Models for Inverse Problems"는 독창적인 방법으로 problem-agnostic한 접근을 택하면서도, problem-specific 방법론에 견줄 만큼 뛰어난 성능을 보여줍니다. 특히, problem-agnostic한 방법은 사전에 학습된 diffusion model을 plug-in 방식으로 활용할 수 있어, computational resource 비용이 절감된다는 장점이 있습니다.

Problem formulation

$y = Hx_0 + z, \quad z \sim \mathcal{N}(0, \sigma_y^2 I)$

위와 같은 함수 $H$와 노이즈 $z$를 통해 $x_0$가 $y$로 변환됩니다. 이때 inverse problem에서는 $y$만이 관찰 가능(measurable)하며, $x_0$와 $z$는 관찰할 수 없습니다. 따라서 inverse problem의 목표는, 측정된 $y$만을 활용하여 $x_0$를 복원하는 것입니다.

Reverse Sampling for Diffusion models

한편, diffusion sampling은 위의 식을 따라 reverse sampling이 진행됩니다. 이 과정에서 $\nabla_x \log p_t(x)$ 대신 학습된 score network (pretrained diffusion model)가 활용됩니다. Diffusion model을 이용해 inverse 문제를 해결하기 위해서는, measurement $y$가 주어졌을 때 $\nabla_x \log p_t(x)$ 대신 $\nabla_x \log p_t(x|y)$를 사용하여, $y$의 정보를 더 많이 반영하고 원하는 데이터로 수렴할 수 있도록 컨트롤하는 것이 필요합니다.

Bayes' rule & Approximation

reverse sampling에서 중요한 역할을 하는 $\nabla_{x_t} \log p_t(x_t | y)$는 베이즈 법칙에 따라 다음과 같이 표현할 수 있습니다:

$\nabla_{x_t} \log p_t(x_t | y) = \nabla_{x_t} \log p_t(x_t) + \nabla_{x_t} \log p_t(y | x_t)$

이때, 첫 번째 항인 $\nabla_{x_t} \log p_t(x_t)$는 학습된 score network $S_\theta(x_t; \sigma_t)$로 근사할 수 있습니다.

$\nabla_{x_t} \log p_t(x_t) \approx S_\theta(x_t; \sigma_t)$

두 번째 항인 $\nabla_{x_t} \log p_t(y | x_t)$는 가이던스 텀(guidance term)으로, 아래의 수식과 같이 근사할 수 있습니다:

$\nabla_{x_t} \log p_t(y | x_t) \approx \left( (y - H\hat{x}_t)^\top \left( r_t^2 H H^\top + \sigma_y^2 I \right)^{-1} H \frac{\partial \hat{x}_t}{\partial x_t} \right)^\top$

위 수식에서:

• Vector: $(y - H\hat{x}_t)^\top \left( r_t^2 H H^\top + \sigma_y^2 I \right)^{-1} H$
• Jacobian: $\frac{\partial \hat{x}_t}{\partial x_t}^\top$

$\sigma_y$가 0인 noiseless assumption을 추가하면 아래와 같이 pseudo-inverse operator를 활용해서 나타낼 수도 있습니다.

$\nabla_{x_t} \log p_t(y | x_t) \approx r_t^{-2} \left( \left( H^\dagger y - H^\dagger H \hat{x}_t \right)^\top \frac{\partial \hat{x}_t}{\partial x_t} \right)^\top, H^\dagger = H^\top (H H^\top)^{-1}$

여기서, $r_t$는 시간에 따라서 점점 증가하도록 heuristic 하게 설계되었습니다.

Approximation Details

아래의 식이 유도되는 과정을 좀더 자세하게 설명해보겠습니다.

$\nabla_{x_t} \log p_t(y | x_t) \approx \left( (y - H\hat{x}_t)^\top \left( r_t^2 H H^\top + \sigma_y^2 I \right)^{-1} H \frac{\partial \hat{x}_t}{\partial x_t} \right)^\top$

DPS: Diffusion Posterior Sampling for General Noisy Inverse Problems
에서 probablistic graph를 설명하며 아래와 같은 관계를 이끌어 냈던 적이 있죠.

$p_t(y | x_t) = \int_{x_0} p(x_0 | x_t) p(y | x_0) dx_0$

본 논문에서는 $\mathcal{N}(\hat{x}_t, r_t^2 I)$로 $p_t(x_0 | x_t)$를 근사합니다.

$p_t(x_0 | x_t) \approx \mathcal{N}(\hat{x}_t, r_t^2 I)$

$x_t$가 주어졌을때 $x_0$를 tweedi formula를 활용해 point estimation 할 수 있습니다. 이를 $\hat{x}_t$ 으로 표기합니다.

$\hat{x}_t = \mathbb{E}[x_0 \mid x_t] = x_t + \sigma_t^2 \nabla_{x_t} \log p_t(x_t) \approx x_t + \sigma_t^2 S_\theta(x_t; \sigma_t) \quad \text{(Tweedie's Formula)}$

이때, multivariate Gaussian distribution의 수식 전개를 활용하여 아래의 관계를 도출할 수 있습니다. Gaussian distribution은 평균(mean)과 분산(variance)만으로 전체 분포를 설명할 수 있기 때문에, 이 두 가지를 구하는 데 집중하면 쉽게 이해할 수 있습니다.

$p_t(y | x_t) \approx \mathcal{N}(H\hat{x}_t, r_t^2 H H^\top + \sigma_y^2 I)$

이를 미분하면 원래 설명하고자 했던 approximation과 일치한다는 것을 확인할 수 있죠.

DDIM Reverse Sampling Process

한편, 본 논문에서는 one step (iterative reverse process의 for loop element step)을 DDIM의 sampling 방식을 활용했습니다. 따라서 DDIM의 sampling process를 확인해두는 것이 좋을 것 같아 첨부해봤습니다.

Reverse Sampling process

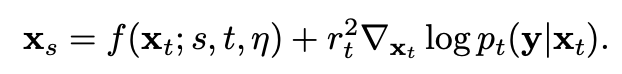
$f$는 DDIM reverse sampling 과정과 완전히 일치하며, pseudo guidance term에 $r_t^2$을 곱하여 $x$를 denoise해 나갑니다. 이때 $r_t^2$을 곱하는 것은 heuristic한 디자인이며, 직관적으로 이는 guidance term의 영향을 $\sigma_t$의 term에 independent 하도록 하려는 의도로 해석할 수 있습니다. (최종 알고리즘에선 단위 guidance에 적절한 weight을 곱해 더하도록 디자인 되어있음.)

아래의 그림에서 heuristic design의 sample quality를 비교합니다. 본 논문에서 제안한 (heuristic) weight의 정당성을 어필합니다.

$\hat{x}_t$는 $x_t$를 활용해 노이즈를 예측하고, 이를 바탕으로 $x_0$의 추정치를 계산한 것입니다. DDIM에서 사용되는 $\sqrt{\alpha_s}$, $c_1$, $c_2$는 각 항의 가중치로, 이를 통해 이미지가 노이즈 예측을 통해 계산됩니다. 본 논문에서 제안하는 guidance term은 $\sqrt{\alpha_t}$로 스케일링되는데, 이는 Variance Exploding (VE) SDE를 Variance Preserving (VP) SDE로 변환하는 과정에서 rescaling된 값입니다. $\alpha_t$는 시그널의 가중치를 나타내며, reverse process에서 시간이 $t$가 감소함에 따라 $\alpha_t$가 점점 커지므로, guidance의 영향력도 for loop을 반복하면서 점점 커집니다.

따라서, DDIM 기반의 sampling에서 measurement $y$에 대한 제어를 pseudo guidance를 통해 수행했다고 해석할 수 있습니다. 다만, 이 guidance term을 계산하는 과정이 computationally expensive하다는 점이 논문의 한계로 지적되고 있습니다.

다른 guidance model과의 비교

논문에서 첨부된 table에서 확인할 수 있듯이 Pseudoinverse guidance는 $y$가 $x_t$에 대해서 미분가능하지 않은 경우도 취급할 수 있다는 장점이 있습니다. 그 뿐만 아니라, Pseudoinverse operator가 reconstruction guidance에서 활용되었던 transpose operator 보다 훨씬 정교한 연산을 수행할 수 있다고 어필하고 있습니다. 더불어, $p(x_0|x_t)$가 $H$ operator에 대해서 independent하여 consistent하다고 합니다.

실험 결과

super resolution과 inpainting task에서 problem-specific method (각 task dataset에 대해서) training 와 비교를 진행했습니다. 그 결과 본 논문에서 제시된 problem-agnostic method가 생산한 이미지의 퀄리티(FID)가 problem-specific method과 견줄만하다는 결론을 이끌어냈습니다. 게다거, ablation study를 통해서 pseudo guidance와 adaptive weight의 영향력을 입증했습니다.

제안된 방법은 별다른 training 없이도 problem에 대해서 training을 진행한 방법과 성능을 나란히 한다는 점과 non-differential function y에 대해서도 문제를 풀 수 있다는 점에서 의미가 깊습니다. 다만, pseudoinverse operator의 계산으로 인해 속도 측면에서 개선되어야할 점이 있다고 합니다.

끝~