[Deep Learning] 기계학습과 MLE 관계

관점의 차이

일반 딥러닝 태스크에서는, 우리가 원하는 출력 $f_\theta (x)$가 정답과 가까워지는 것을 목표로 한다.
이를 위해 역전파를 이용할 때에는 출력 $f_\theta (x)$과 정답 $y$의 차이를 Loss Function이라고 정의하고, 두 값의 차이를 줄이는 방향으로 학습을 진행한다.

MLE 관점으로 볼 때는
네트워크 출력 값(확률 분포) $f_\theta (x)$ 가 주어졌을 때, 정답 $y$가 나올 확률(Likelihood)가 최대가 되기를 목표로 한다.

즉, Deep Neural network $f_\theta (x)$뿐만 아니라, 분포 $p(*|f_\theta (x))$가 어떤 분포를 따를 지 가정하고 가야한다.

VAE

전반적인 VAE의 간단 설명

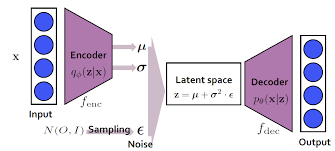
VAE를 학습할 때는 maximum likelihood 접근법을 사용한다. 즉, $p_\theta (x)$를 maximize하는 $\theta$를 찾는 것을 목적으로 한다.

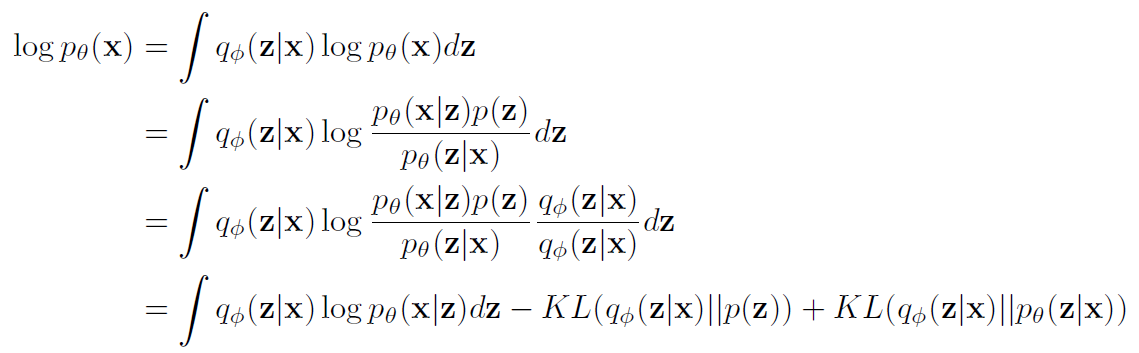
VAE의 maximum likelihood 증명

위의 식 중 마지막 식을 maximize하는 parameter $\theta$를 찾으면, 우리가 원하는 Likelihood를 maximize하는 parameter를 찾을 수 있다.

decoder에서 MLE 사용?

---

Logistic 함수

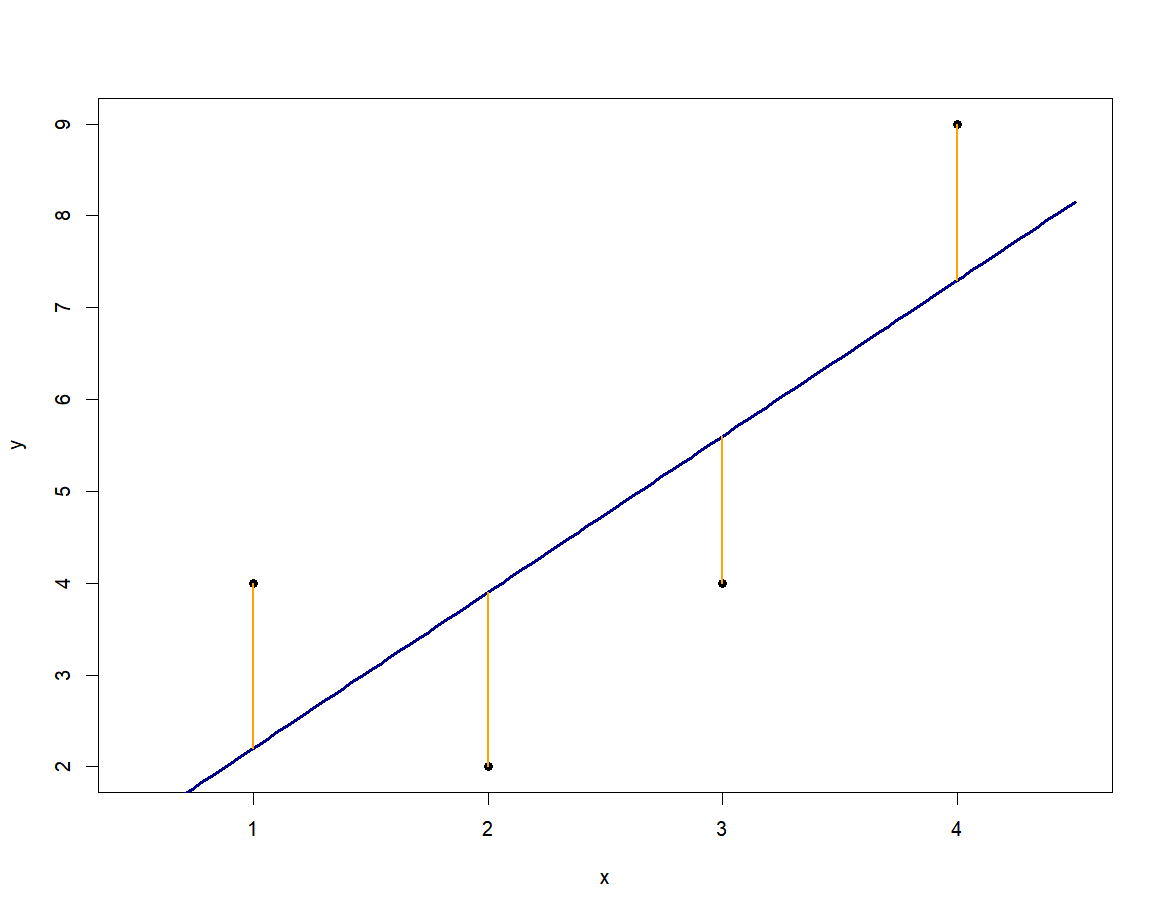
선형 회귀 분석에서 회귀 계수를 구하는 방법으로 최소 제곱법을 사용한다.
데이터를 가장 잘 설명할 수 있는 직선을 그리는 것으로 즉, 아래 그림에 오렌지 색 선분 길이 제곱의 합이 최소화되는 직선을 찾는 것이다.

실제 많은 자연, 사회현상에서는 특정 변수에 대한 확률값이 선형이 아닌 S-커브 형태를 따르는 경우가 많다. 이러한 S-커브를 함수로 표현해낸 것이 바로 로지스틱 함수이다. 시그모이드 함수라고 불리기도 한다.

$y = \frac{1}{1+e^{-x}}$

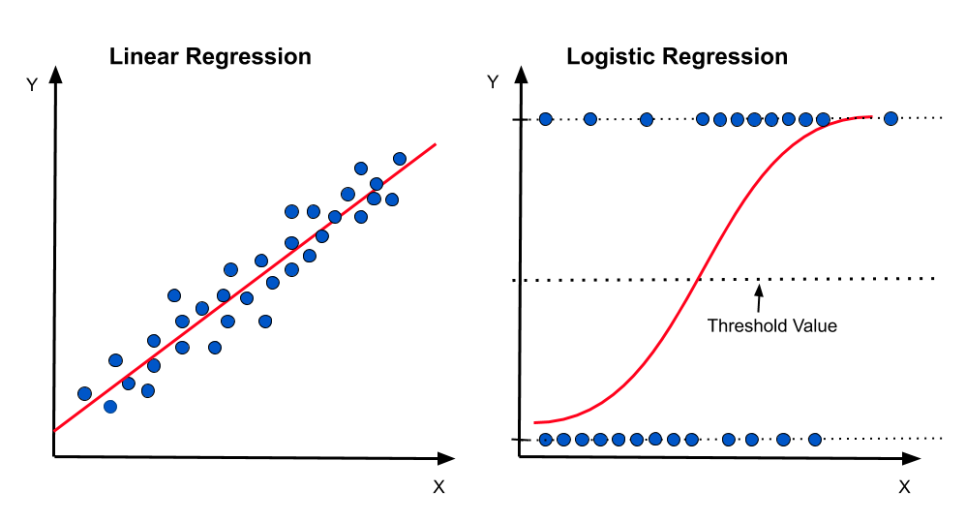
로지스틱 회귀는 베루누이 시행(Bernoulli trial)을 전제로 하는 모델이다.

*베로누이 시행이란? 어떤 실험이 두 가지 결과만을 가지는 실험을 가리킨다. 베르누이 시행의 결과에 따라 0(실패) 또는 1(성공)의 값을 대응시키는 확률변수를 베루누이 확률변수라고 합니다.

Logistic 함수에서의 Maximum Likelihood Estimation

로지스틱 회귀는 log likelihood 함수가 최대가 되는 파라미터 $\beta$를 결정하는 과정이다.

$L=\prod _{i}^{ }{{\sigma({\beta}^{T}\overrightarrow{{x}_{i}})}^{{y}_{i}}{\left\{1-\sigma({\beta}^{T}\overrightarrow{{x}_{i}})\right\}}^{1-{y}_{i}}}$

학습데이터에 관측치 $i$개가 있고, 정답 범주가 2개(0 혹은 1)인 이항로지스틱 모델의 parmeter $\beta$가 주어졌다고 가정한다. 그러면 $i$번째 관측치의 종속변수 $y_i$는 $\sigma({\beta}^{T}{x_i})$의 확률로 1, ${1-\sigma({\beta}^{T}{x_i})}$의 확률로 0이 된다.
*여기서 $x_i$는 $i$번째 관측치의 독립변수, $\sigma$는 로지스틱 함수를 가리킨다.

로지스틱 회귀의 parameter $\beta$는 MLE로 구하게 된다. 로그 우도함수(log-likelihood function)을 최대로 하는 회귀계수 $\beta$는 동시에 우도(likelihood)를 최대화하는 $\beta$이며 그 역도 성립한다.

log likelihood 함수 과정

$L=\prod _{i}^{ }{{\sigma({\beta}^{T}\overrightarrow{{x}_{i}})}^{{y}_{i}}{\left\{1-\sigma({\beta}^{T}\overrightarrow{{x}_{i}})\right\}}^{1-{y}_{i}}}$
$\ln{L} =\sum_{i}^{}{{y}_{i}\ln{\left\{\sigma({\beta}^{T}{\overrightarrow{x_{i}}})\right\}}}+\sum_{i}^{}{\left(1-{y}_{i}\right)\ln{\left\{1-\sigma({\beta}^{T}{\overrightarrow{x_{i}}})\right\}}}$

로그 우도함수는 추정 대상 parameter인 회귀계수 $\beta$에 대해 비선형이기 때문에 선형회귀 모델과 같이 명시적인 해가 존재하지 않는다.
따라서 Stochastic Gradient Descent(SGD)와 같은 반복적이고 점진적인 방식으로 해를 구하게 된다.

Reference

• KL divergence 설명 (Relative entropy 설명, KL divergence와 MLE)
• 로지스틱회귀 파라메터 추정