최근에 접한 문제 중에서 가장 이해하기 어려운 문제였다.
얼핏 단순한 DP 문제로 보이지만, 실제로는 비트마스킹 기법을 적용해야 풀 수 있는 문제이다.
1. 문제 이해
현재 자릿수에서 숫자 n에 도착했다고 가정하자.
아마 바로 전 자릿수의 n - 1 또는 n + 1에서 왔을 것이다. (물론 이전 숫자가 0이었다면 1로만, 9였다면 8로만 갈 수 있다)
현재 단계의 숫자 n에서의 경우의 수는, 바로 이 둘을 합친 값이 될 것이다.

보통은 여기까지만 고려해도 되지만, 이 문제에는 '최종적으로 0부터 9까지의 모든 숫자를 방문해야 한다'라는 조건이 있다.
즉, 각 자릿수의 숫자들마다 '지금까지 어떤 숫자들을 거쳐왔는지'를 기억할 필요가 있다.
만약 이를 집합 자료구조로 나타내고자 하면, 모든 고유한 경로마다 하나씩 자신의 집합을 가지게 될 것이고, 결국 현재 자릿수의 특정 숫자에 도착하는 경로는 여러 개이므로 수많은 집합들을 배열 형태로 가지게 될 것이다. (그리고 이는 팩토리얼 형태이므로 메모리 초과가 뜰 것이다)
그렇다면 방문한 숫자들에 대한 정보를 다른 방식으로 표현할 수 있을까?
2. 비트마스킹이란?
비트마스킹은 정수의 이진수 표현 자체를 자료구조로 이용하는 기법이다.
0과 1, 두 가지 상태를 나타내는 개별 비트들을 여러 개 모아 사용한다는 점은 흔히 사용되는 visited[N] 같은 배열과 비슷하지만, 여러 개의 비트들을 '하나의 십진수 값'으로 해석할 수 있다는 점이 가장 큰 차이점이다. (또한, 비트 연산은 일반적인 연산보다 훨씬 빠르므로 시간복잡도 측면에서도 유리하다)
0부터 9까지 각 숫자에 대한 방문 여부의 경우의 수는 총 2^10 = 1024가지이므로, 이 문제에서는 방문한 숫자들에 대한 정보를 비트마스크 형태로 표현할 것이다.
예를 들어, 이진수 0000000000은 십진수로 0이고 이는 '0'부터 '9'까지의 숫자 중 아무것도 방문하지 않았음을 뜻한다. 반면 0000000001은 숫자 '0'을 방문했음을, 00000000101은 숫자 '0'과 '2'를 둘 다 방문했음을 나타낸다.
만약 0부터 9까지 10개의 숫자를 전부 방문했다면 10개의 비트가 모두 1이 되어 1111111111, 십진수로 1023이 될 것이다.
3. 문제 적용
다시 문제로 돌아와서, 현재 자릿수에서 숫자 k에 도착했다고 가정하자. 똑같이 이전 자릿수의 숫자 k - 1 또는 k + 1에서 왔을 것이다.
이제는 추가적으로 지금까지 방문한 숫자들에 대한 정보까지 고려해야 한다.
일단 확실한 것은, 현재 숫자 k를 방문했으므로 방문 기록에 k를 추가해야 한다. 이것은 '지금까지 방문한 숫자 집합'을 나타내는 비트마스크에 (1 << k)을 OR 연산함으로써 수행할 수 있다.
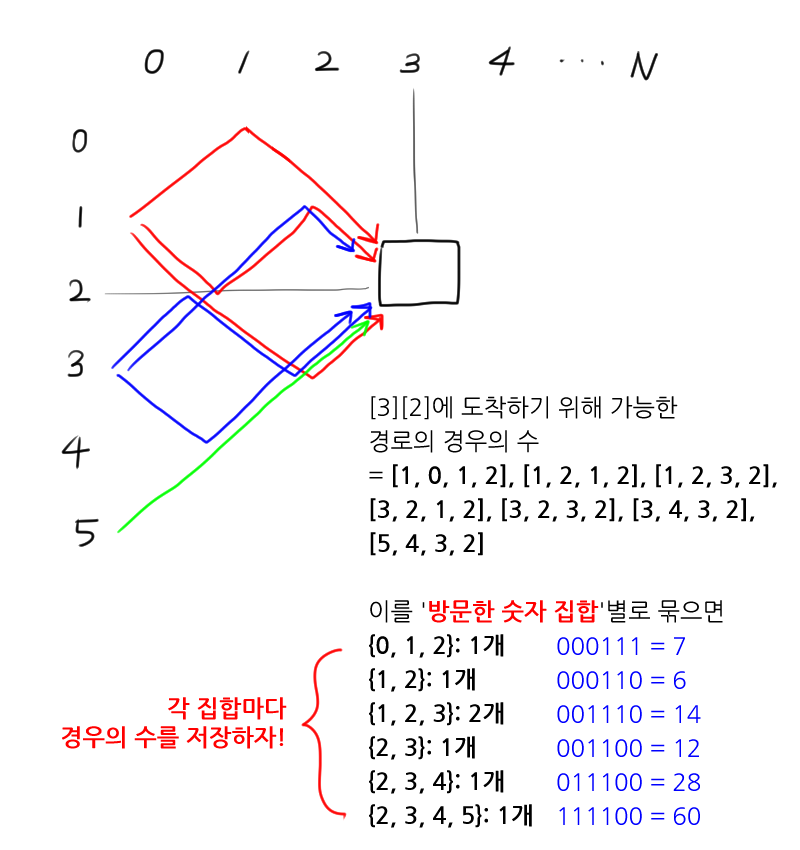
이때 같은 숫자들을 방문했더라도 서로 다른 경로를 통해 왔을 수 있으므로, 각 방문 집합에 따라 경로의 수를 저장할 수 있어야 한다.
그러기 위해서는 '지금까지 방문한 숫자 집합'을 DP 배열의 3번째 차원 인덱스로 표현하고, (dp[i][k][0~1023]) 해당 인덱스에 가능한 경로의 수를 값으로 저장하면 된다.
더욱 쉬운 이해를 위해 그림으로 예시를 들어보았다.
수도 코드로 표현하면 대충 이렇다.
자릿수 1부터 N까지:
이동 가능한 숫자 1부터 9까지:
가능한 방문 집합 비트 0부터 1023까지:
dp[현재 자릿수][현재 이동한 숫자][이전 방문 집합 OR 현재 선택한 숫자]
+= dp[이전 자릿수][이전에 선택한 숫자][이전 방문 집합]그리고 최종적으로 우리가 원하는 값은 sum(dp[N - 1][k][1023]) for k in range(10)이 될 것이다.
[N - 1]= 마지막 자릿수까지 읽었을 때[k]= 마지막으로 도착한 숫자 (0부터 9까지 모두 고려)[1023]= 이진수로1111111111, 즉 0부터 9까지 모든 숫자를 최소 한 번씩 방문한 경우
코드
import sys
input = sys.stdin.readline
N = int(input())
dp = [[[0 for _ in range(1 << 10)] for _ in range(10)] for _ in range(N)]
# dp[x][y][z] = 자릿수 x까지 봤을 때, 현재 숫자로 y를 선택한 경우, 비트 z에 해당하는 숫자들을 방문했을 때, 경우의 수
mod = 1000000000
res = 0
for k in range(1, 10): # 0은 제외하고
dp[0][k][1 << k] = 1 # 초기 경우의 수는 1 (k를 방문함도 동시에 표시)
for i in range(1, N): # 각 자릿수에 대해
for k in range(10): # 0에서 9까지의 숫자 방문
for bit in range(1024): # 이때, 모든 방문 기록 경우의 수를 고려
# bit | (1 << k) == 이전 방문 기록(bit)에 현재 숫자 방문 기록을 추가(| (1 << k))
if k - 1 >= 0:
dp[i][k][bit | (1 << k)] += dp[i - 1][k - 1][bit]
if k + 1 <= 9:
dp[i][k][bit | (1 << k)] += dp[i - 1][k + 1][bit]
dp[i][k][bit | (1 << k)] %= mod
for k in range(10): # 마지막으로 도착한 숫자 (0~9)
res += dp[N - 1][k][1023] # 0부터 9까지 모든 숫자를 방문했을 때, 1111111111(2) = 1023
res %= mod
print(res)