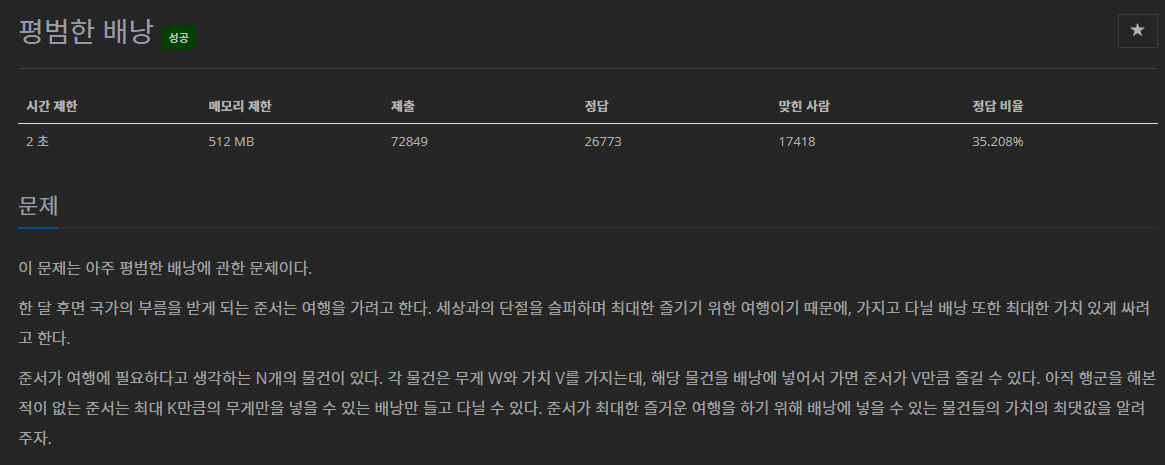
각각의 가치와 무게를 지닌 아이템들을 정해진 중량 내에서 최대의 가치가 되도록 선택하는 냅색 알고리즘 문제이다.
가장 먼저 떠올린 것은 백트래킹을 이용하여 모든 아이템의 모든 조합의 수를 따져보는 방법이었지만, 시간복잡도가 기하급수적으로 커지므로 쓸 수 없었다.
다음으로 떠올린 것은 DP로 푸는 방법이었는데, 여기서 DP의 '기준점'을 무엇으로 잡아야 하는지가 문제였다.
- 기준을 '아이템의 개수'로 둔다. (예 - 아이템이 1개일 때 최대 가치가 되는 경우, ...)
- 기준을 '배낭의 최대 허용 중량'으로 둔다. (예 - 중량이 1일 때 최대 가치가 되는 경우, 중량이 2일 때 최대 가치가 되는 경우, ...)
- 기준을 'i번째 아이템까지 살펴보았을 때'로 둔다. (예 - 1번째 아이템까지 살펴보았을 때 최대 가치가 되는 경우, ...)
등등...
어떤 문제를 DP로 풀기 위해서는 특정 값을 기준으로 현재의 최적값이 과거의 최적값을 통해 설명될 수 있어야 한다. 하지만 이 문제의 경우 기준을 하나만 두어서는 점화식을 만드는 것이 불가능했다. (예 - 가방의 무게가 같더라도 그 안에 넣은 아이템의 종류에 따라 미래의 가치가 달라질 수 있음)
해결법은 '조건'을 여러 개로 두는 것, 즉 다차원 배열을 이용하는 것이다.
위에 써놓은 조건 중 2번(배낭의 중량)을 행(i)으로, 3번(i번째 아이템 탐색)을 열(j)으로 둔 2차원 행렬을 생각해 보자.
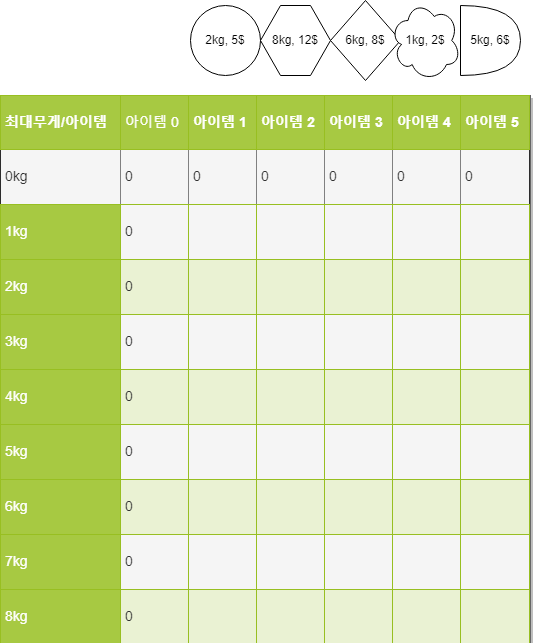
위의 행렬을 dp라 하면, dp[i][j] == (배낭의 최대 무게가 i이고, j번째 아이템까지 살펴봤을 때의 최대 가치)로 해석할 수 있다.
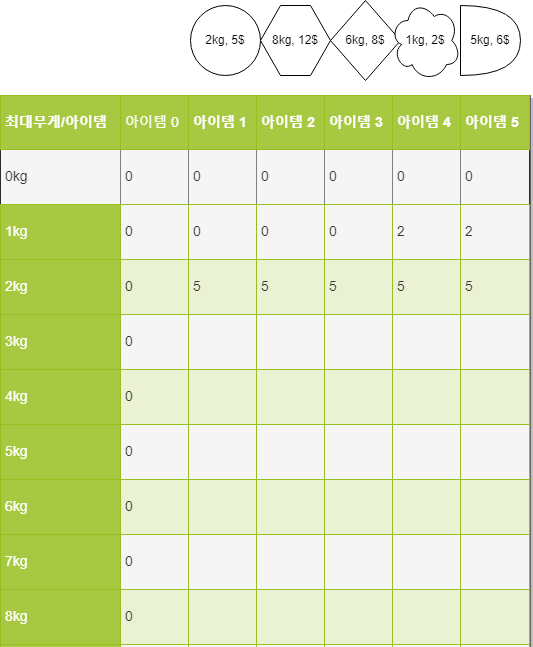
이때 dp[i]는 배낭의 최대 무게가 0인 경우, dp[j]는 아무 아이템도 고려하지 않은 경우이므로 값이 전부 0이 된다.
먼저 배낭의 무게가 1kg일 때 아이템을 하나씩 살펴보자.
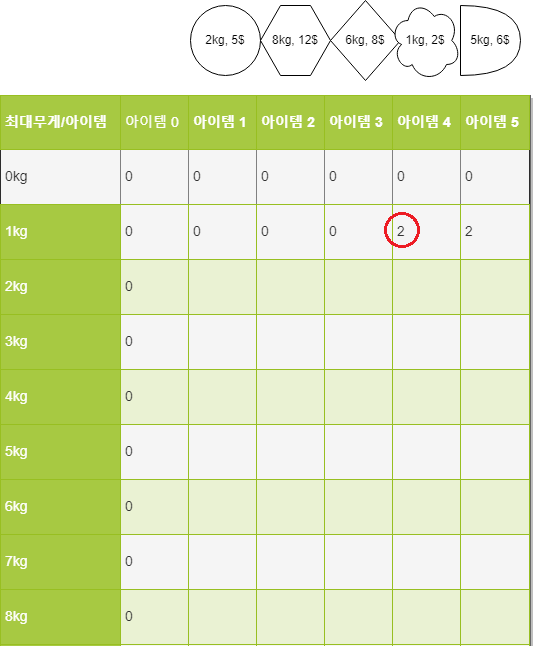
1kg 짜리 배낭에 넣을 수 있는 아이템은 4번째뿐이다. 일단 넣을 수 있다면 무조건 넣고 본다.
그렇다면 만약 여기서 더 많은 아이템을 살펴봤을 때,
'더 좋은 경우의 수'가 있다면 어떻게 해야 할까?
이미 배낭은 적당히 찼는데, 적은 무게와 높은 가치를 지닌 아이템이 등장했다면...
답은 과거로 돌아가서 가정해보는 것이다.
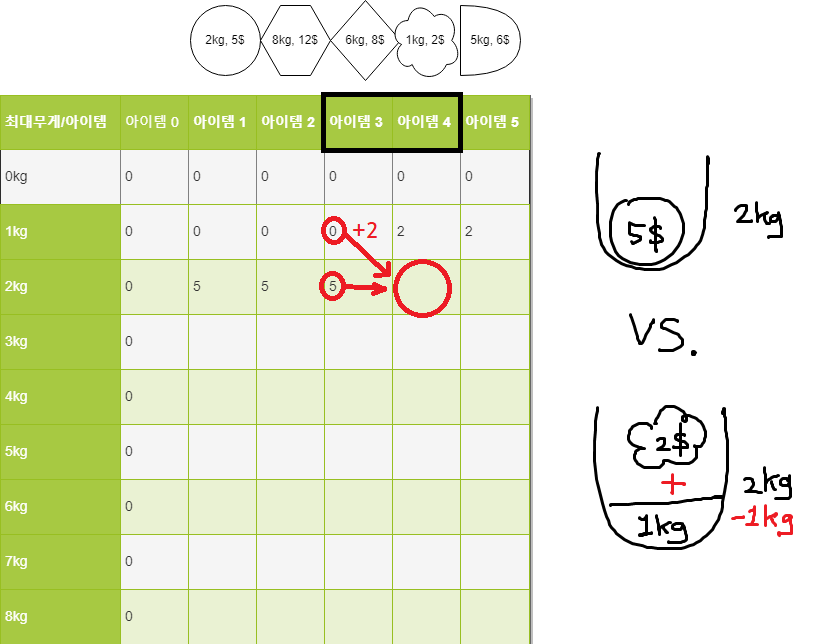
현재 보고 있는 아이템을 담지 않고 넘어갈 때의 가치 vs.
'현재 아이템이 담길 수 있었던 때'에서 현재 아이템을 담을 때의 가치
현재 배낭의 최대 무게(i)가 2이고, 가득 찼으며(w == 2), 담긴 가치(v)가 5인 상황에서,
현재 보고 있는 4번째 아이템의 무게가 1kg이므로, 이 아이템을 담을 수 있으면서도 최대한 채워놓은 배낭의 무게는 2kg - 1kg = 1kg일 것이다. 또한 4번째 아이템을 담기 직전의 상황은 3번째 아이템까지 살펴보았을 때를 의미한다. 이때의 가치는 dp[1][3]에 담겨있다. 여기에 4번째 아이템을 담는다면 가치는 dp[1][3] + 2 = 2가 된다.
만약 4번째 아이템을 담지 않고 넘어간다면 이전 가치값 dp[2][3]을 그대로 유지할 것이다.
결론적으로 dp[i][j] = max(dp[i - weight][j - 1] + value, dp[i][j - 1])이라는 점화식을 도출할 수 있다. (weight, value는 각각 현재 보고 있는 아이템의 무게 및 가치)
물론 이것은 현재 아이템이 배낭의 최대 무게보다 가볍거나 같을 때에만 가능하다. 그렇지 않다면 물건을 다 빼도 담을 수 없으므로 dp[i][j - 1]을 그대로 유지해야 한다.
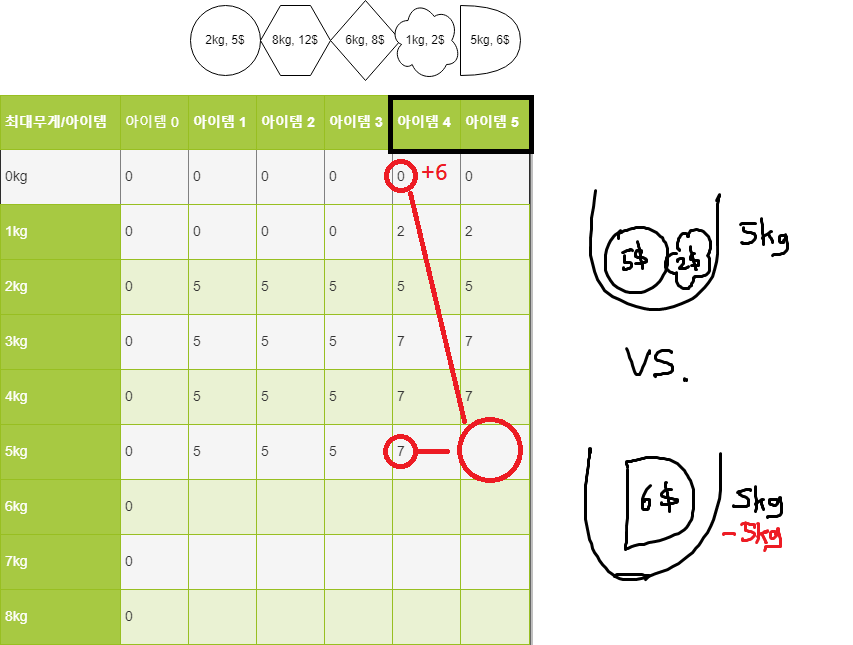
이때는 물건을 담지 않는 것이 가치가 더 높으므로 그대로 5를 써준다. 5번째 아이템은 현재 배낭의 무게를 초과하므로 역시 무시된다.
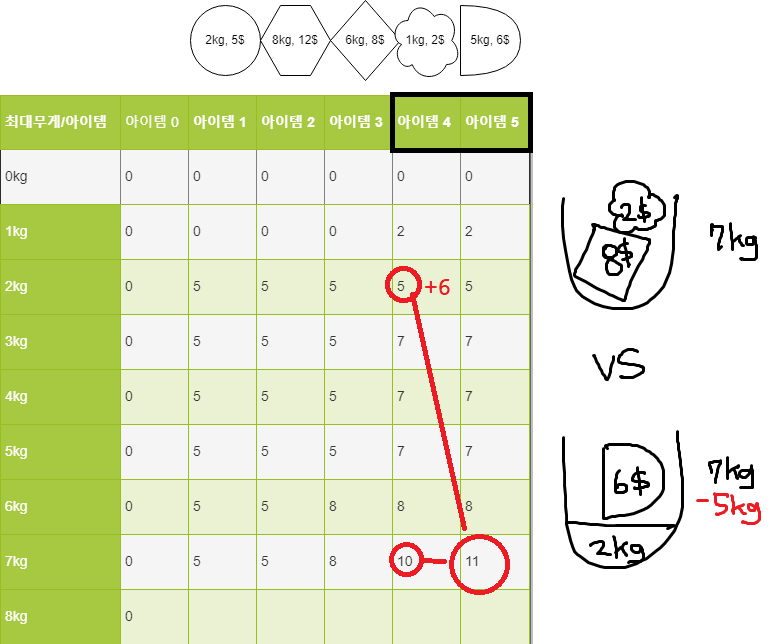
이런 방식으로 계속해서 따질 수 있다.
처음 이 문제를 봤을 땐 풀지 못했다. 2차원 배열 DP 문제를 몇 번 접해보지 않아서 기준을 떠올리는 것부터가 어려웠다. 문제 해설을 봐도 내가 바보여서인지 직관적으로 이해가 잘 되지 않았다...
그래서 각 단계마다 그림을 그려보면서 의미를 파악하려 노력했다. 다행히 지금은 충분히 이해할 수 있게 되었다.
