Inductive bias

꼼댕이·2023년 5월 24일

Variance & Bias

먼저 Error는 다음과 같이 Bias와 Variance로 분해될 수 있습니다.

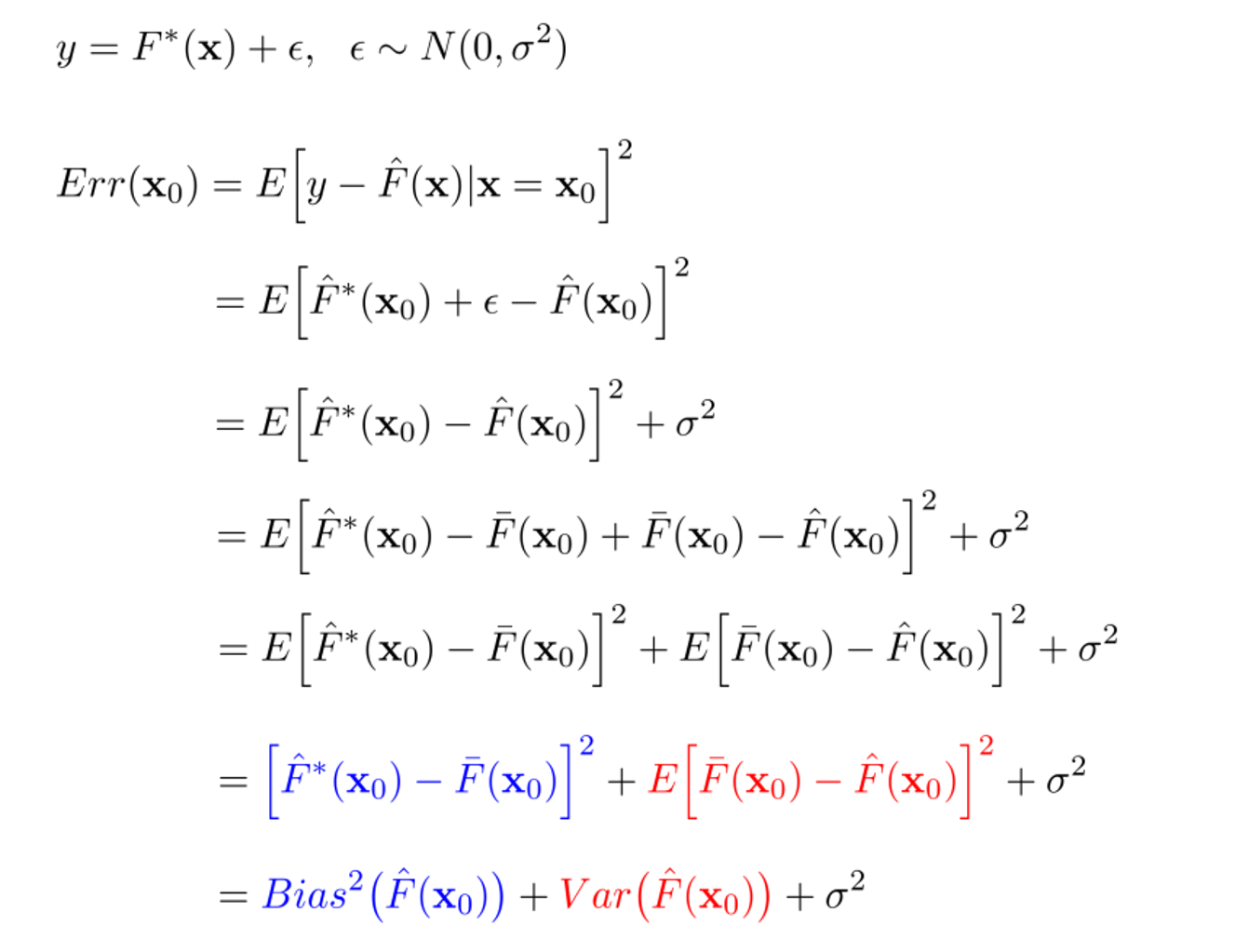
Bias
Bias(의 제곱)은 실제값( $F∗(X0)$ )과 예측값들의 평균(F∗(X0)$)의 차이를 의미합니다. 낮은 Bias는 평균적으로 우리가 실제값에 근사하게 예측을 수행한다는 것을 의미하며, 높은 Bias는 실제값과 예측값의 평균이 멀리 떨어져있음으로 poor match를 의미합니다. 즉, Bias는 모델의 예측값과 실제값이 얼마나 떨어져있는가를 의미하며, Bias가 크게 되면 과소적합(underfitting)을 야기합니다.
Variance
Variance는 예측값들의 평균( $F∗ (X0)$ )으로부터 특정 예측값들( $F(X0$ ))이 어느 정도 퍼져있는 가를 의미합니다. 낮은 Variance는 들어오는 데이터에 따라 예측값이 크게 바뀌지 않는 것을 의미하며, 높은 Variance는 들어오는 데이터에 따라 예측값이 크게 바뀌므로 poor match를 의미합니다. 즉, Variance는 예측 모델의 복잡도라고 해석할 수 있으며, Variance가 큰 모델은 훈련 데이터에 지나치게 적합을 시켜 일반화되지 않는 과대적합(overfitting)을 야기합니다.

Inductive Bias

주어지지 않은 입력의 출력을 예측하는 것이다. 즉, 일반화의 성능을 높이기 위해서 만약의 상황에 대한 추가적인 가정(Additional Assumptions)

일반적으로 모델이 갖는 generalization problem으로는 모델이 brittle(불안정)하다는 것과, spurious(겉으로만 그럴싸한)하다는 것이 있습니다.

Models are brittle : 데이터의 input이 조금만 바뀌어도 모델의 결과가 망가지게 됩니다.
Models are spurious : 데이터 본연의 의미를 학습하는 것이 아닌 결과(artifacts)와 편향(biases)를 학습하게 됩니다.

이러한 문제점들을 해결하기 위해 Inductive Bias를 이용하게 됩니다. Wikipedia에서 정의를 빌려오자면, Inductive bias란, 학습 시에는 만나보지 않았던 상황에 대하여 정확한 예측을 하기 위해 사용하는 추가적인 가정 (additional assumptions)을 의미합니다.

Machine learning에서는 어떤 목표(target)를 예측하기 위해 학습할 수 있는 알고리즘 구축을 목표로 하고, 이를 위해 제한된 수의 입력과 출력 데이터가 주어지게 됩니다. 훈련 데이터를 넘어 다른 데이터에 대해서도 일반화할 수 있는 능력을 가진 모든 기계 학습 알고리즘에는 어떤 유형의 Inductive Bias가 존재하는데, 이는 모델이 목표 함수를 학습하고 훈련 데이터를 넘어 일반화하기 위해 만든 가정입니다.

편향의 관점으로 다시 정의를 내려보자면 모델이 학습과정에서 본 적이 없는 분포의 데이터를 입력 받았을 때, 해당 데이터에 대한 판단을 내리기 위해 가지고 있는, 학습과정에서 습득된 Bias(편향)이라고 말할 수 있을 것 같습니다.

즉 모델을 좀 더 Robust하게 만들기 위함

몇 가지 Inductive Bias를 예로 들어보겠습니다.

Translation invariance : 어떠한 사물이 들어 있는 이미지를 제공해줄 때 사물의 위치가 바뀌어도 해당 사물을 인식할 수 있습니다.
Translation Equivariance : 어떠한 사물이 들어 있는 이미지를 제공해줄 때 사물의 위치가 바뀌면 CNN과 같은 연산의 activation 위치 또한 바뀌게 됩니다.
Maximum conditional independence : 가설이 베이지안 프레임워크에 캐스팅될 수 있다면 조건부 독립성을 극대화합니다.
Minimum cross-validation error : 가설 중에서 선택하려고 할 때 교차 검증 오차가 가장 낮은 가설을 선택합니다.
Maximum margin : 두 클래스 사이에 경계를 그릴 때 경계 너비를 최대화합니다.
Minimum description length : 가설을 구성할 때 가설의 설명 길이를 최소화합니다. 이는 더 간단한 가설은 더 사실일 가능성이 높다는 가정을 기반으로 하고 있습니다.
Minimum features: 특정 피쳐가 유용하다는 근거가 없는 한 삭제해야 합니다.
Nearest neighbors: 특징 공간에 있는 작은 이웃의 경우 대부분이 동일한 클래스에 속한다고 가정합니다.

CNN이 이미지 관련 문제에서 강점을 보이는 이유?

Classification, Object Detection, Semantic Segmentation 등 이미지를 다루는 모델들은 모두 CNN을 사용한다. 왜 CNN이 이미지 관련 문제에서 강점을 보이는 것일까? 바로 CNN이 이미지를 다루기에 적합한 Inductive Bias를 갖고 있기 때문이다. CNN에는 어떤 Inductive Bias가 숨어있는 것일까? FCN과 CNN을 비교해보며 한번 살펴보자.

FCN(Fully Connected Neural Network)은 가장 일반적인 블록의 형태로, 가중치와 편향으로 각 층의 요소들이 서로 모두 연결되어 있다. 즉, 모든 입력의 요소가 어떤 출력 요소던지 영향을 미칠 수 있기 때문에, Inductive Bias가 매우 약하다.

반면에, CNN(Convolutional Neural Network)은 Convolution Filter가 입력을 Window Sliding 하게 된다. CNN의 Entities(Grid Elements, Pixels)는 FCN의 Entities(Elements)와 마찬가지로 개별단위이지만, Entities 간의 관계가 약하다는 차이점이 있다. 이러한 특징으로 CNN은 FCN과 다르게 Locality & Translation Invariance의 Relational Inductive Biases를 갖는다.

여기서, Localitiy는 입력에서 각 Entities간의 관계가 서로 가까운 요소들에 존재한다는 것을 의미한다. 그리고 Translation Invariance란 입력과 동일하게 계속해서 관계가 유지된다는 것을 말한다. 이는 무엇을 의미할까? 어떤 특징을 가지는 요소들이 서로 모여있는지가 중요한 문제에서 좋은 성능을 보여준다는 것을 의미한다. 이러한 이유에서 CNN이 이미지 관련 문제에서 강점을 보이는 것이다.

CNN과 마찬가지로 RNN(Reccurent Neural Network)에서도 유사한 가정이 사용된다. CNN이 공간의 개념을 사용한다면, RNN은 시간의 개념을 사용하는 것이다. RNN에서는 CNN의 Locality & Translation Invariance와 유사한 개념으로 Sequential & Temporal Invariance의 Relational Inductive Biases를 갖는다. Sequential이란 입력이 시계열의 특징을 갖는다고 가정하며, Temporal Invariance는 동일한 순서로 입력이 들어오면 출력도 동일하다는 것을 말한다.

마찬가지로 GNN(Graph Neural Network)은 이러한 개념을 그래프로 가져간 것으로, Permutational Invarianced의 Relational Inductive Biases를 갖는다. 이러한 가정들의 장점은 가정이 맞는 경우 좋은 성능을 보여준다는 것이다. 하지만, 가정이 맞지 않는 경우에는 매우 약한 모습을 보여준다.

CNN vs Transformer

Transformer는 NLP분야 뿐만아니라 최근에는 CV에서도 강력한 성능을 보여주며, 주목을 받고 있다. 그렇다면, 항상 Transformer를 사용하는 것이 좋을까? CNN은 이미지가 지역적으로 얻을 정보가 많다는 것을 가정하고 만들어진 모델이다. 반면에, Transformer는 Positional Embedding과 Self-Attention을 사용해 모든 정보를 활용한다. 즉, Transformer는 CNN에 비해 Inductive Biases가 부족하다고 볼 수 있다. 결과적으로 Global한 정보가 필요한 경우에는 Transformer가 좋지만, Inductive Biases가 잘 맞는 이미지가 지역적으로 얻을 정보가 많은 경우에는 CNN이 적합하다는 것을 알 수 있다.