이전 게시글 내용에서 온다!
Homomolphism의 image
사실 homomolphism은 ring R에서 ring S로 가는 하나의 연산관계를 보존하는 함수이지 그 결과물들 즉, image가 ring이 될지에 대해서는 아직 얘기하지 않았다. 그 답이 아래 Cor3.11에 있다.
homomolphism R->S의 image는 항상 S의 subring이다!
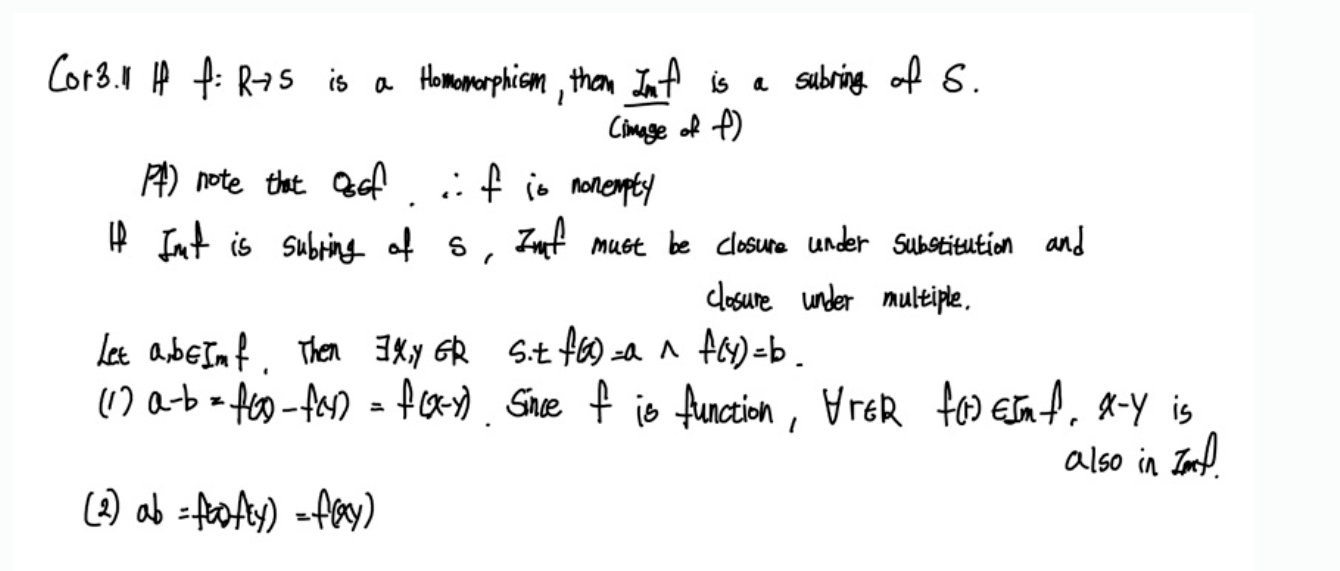
Existance of Isomolphism
우리는 어떤 두 ring사이에 Isomolphism이 존재하는지 알고 싶다.
Isomolphism이라는 건 대수적으로 완전히 같다는 의미이기 때문! 근데 어떻게 알 수 있을까? 그건 모른다.
하지만 두 개 사이에 Isomolphism이 존재하지 않음은 보일 수가 있다!
여러 사실들, 만약 Isomolphism이 존재해야 한다면 성립해야할 invariant, 즉 변치않는 사실들에 대해 알아보자.



1. Cardinality
가장 기본적인 사실이다. 두 set간에 bijection이 존재하려면 최소한 집합의 크기가 같아야한다. 자연수 집합 N에서 실수집합 R로의 bijection이 존재할 수 없듯 말이다.
2.number of zerodivisor
Isomolphism은 결국 대수적인 성질을 구분할 수 없다는 의미이다. 그러면 당연히 zerodivisor의 수도 같아야 하지 않겠는가?
위의 증명 2개는 zerodivisor은 zerodivisor가 되며 zerodivisor가 아닌 수는 zerodivisor가 아니게 된다는 증명이다. 2번째 증명에서 α가 0이 아니라는 것이 빠졌다.
3.number of units
Isomolphism은 대수적 성질을 구분할 수가 읎다.
4.additive order
additive order란 어떤 숫자를 계속 더한다고 했을 때 제일 적게는 몇 번을 더해야 0이 될까? 를 묻는 것이다. 예를 들어 Z6에서 2는 3번을 더했을 때 0이 된다.
