열심히 올리는 현대대수
1.현대대수 공부1

well-ordering을 이용한 divisibillity와 gcd에 관한 논의입니다. gcd(a,b) = au+bv 꼴로 표현할 수 있다는 내용과 division algorithm이 가장 중요한 내용입니다. 특히 gcd에 관한 내용은 gcd의 명제들을 증명하기에 아주
2.1.2, 1.3 Divisibility, prime and unique factorization

1.gcd(a,b)가 a와 b의 linear combination으로 이루어질 수 있다는 증명.(이전 내용에 기록)2.Thm1.4는 참 중요하다.p가 bc를 나눌 때 b를 나누지 못하면 c를 나누고 c를 나누지 못하면 b를 나눈다.3.Thm1.5 (=>)p가 prime
3.2.1 Congruence and Congruence classes

핵심은 modulo 연산으로 집합을 나누었을 때 equivalent class로 나눌 수 있고 set을 partition할 수 있다! 라는 것이다
4.2.3 The Structure of Zp and Zn

Zp는 항상 a가 0이 아닐 때 ax=1의 해가 존재한다. 이 때 a를 unit이라고 부른다. (Zp는 추후 field라는 명칭으로 부를 것이다!) 또 ab = 0 이면 a가 0이거나 b가 0이다.(추후 Integral Domain이라고 부른다.) 요놈은 zerodiv
5.3.1 Definition of Rings

Ring과 그 성질 1번
6.3.2 Basic properties of rings

ring의 성질! integral domain과 field의 관계성!
7.3.3 Isomorphism and Homomorphism 1

현대대수는 프로그래밍의 뭐랑 연관이 깊을까. 연산자 오버로딩? 이건 너무 직접적인 관계인가 ㅋㅋㅋ 하여튼 오늘도 시작해보도록 하자. Definition of Isomolphism Isomolphism sketch isomolphism은 굉장히 좋은 성질로 대수적으로
8.3.3 Isomolphism and Homomorphism 2
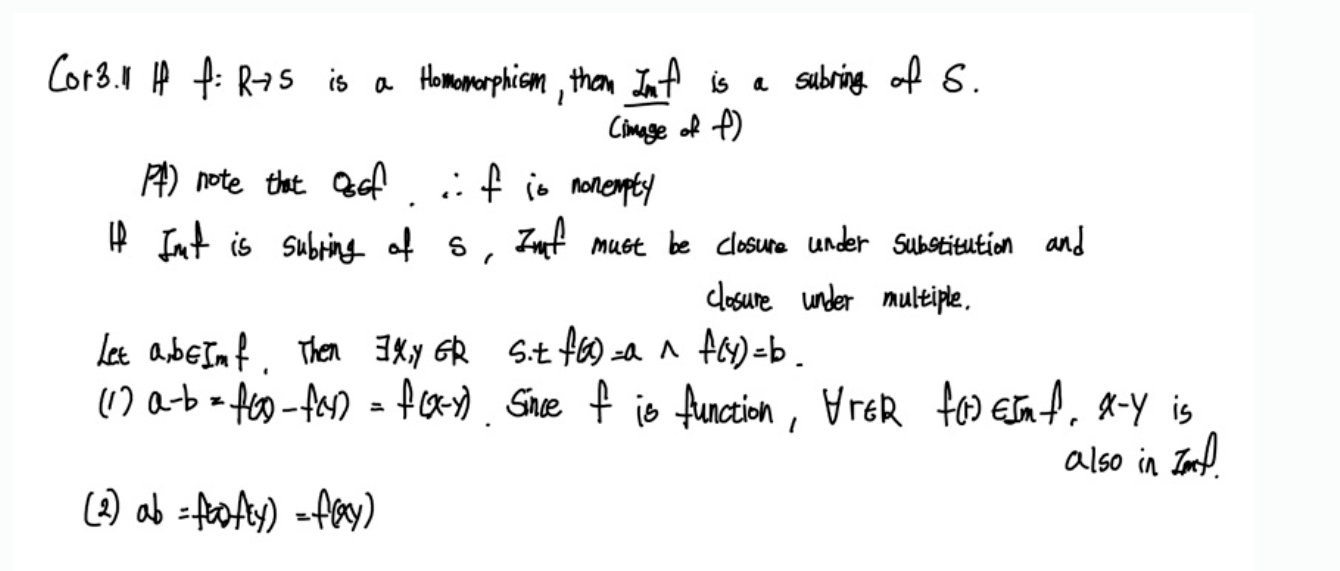
이전 게시글 내용에서 온다! 사실 homomolphism은 ring R에서 ring S로 가는 하나의 연산관계를 보존하는 함수이지 그 결과물들 즉, image가 ring이 될지에 대해서는 아직 얘기하지 않았다. 그 답이 아래에 있다. > homomolphism R->
9.4.1 Division algorithm for Polynomials, 4.2 Divisibillity

4장 polynomial arithmetic 계수가 ring의 원소인 polynomial들을 생각하고 그 연산에 대해 공부하자!
10.4.3 Irreducibles and Unique Factorization

다항식에서의 소수와 인수분해에 대해 알아봅시다!
11.4.4 Polynomial functions, roots and reducibility

n차 방정식의 근은 왜 최대 n개일까? 2,3차 방정식의 근이 없다는 것은 어떤 의미를 가질까? 한 번 알아보자.
12.4.5 Irreducibility in Q[x]

유리수 다항식과 정수 다항식은 사실 긴밀한 관계가 있습니다. 두 다항식의 인수분해는 연결돼 있는데요? 같이 확인해봅시다.
13.5.1,5.2 Congruence in F[x], Congruence class arithmetic

다항식에서도 합동관계를 찾아봅시다!!!
14.5.3 The Structure of F[x]/p(x) when p(x) is irreducible

F[x]/p(x)에 대해 알아봅시다. 특히 p(x)가 prime일 때!
15.6.1 Ideals and congruence(1)

Ideal을 정의함으로 congruence를 일반화해봅시다. 우리의 궁극적 목표는 Quotient ring입니다.
16.6.1(2),6.2 Quotient Rings and Homomorphism

Quotient ring과 ideal의 관계를 알아봅시다.
17.6.2 Quotient Rings and Homomorphisms2

first isomolphism theorem
18.6.3 Prime ideal and Maximal ideal

R/I가 integral domain이 되기 위한 조건! 그리고 field가 되기 위한 조건!
19.7.1 Definition and Examples of Groups

드디어 군입니다. 군 즉, group의 정의와 다양한 예시들을 살펴봅시다!
20.7.2 Properties of groups

group의 성질에 대해서 살펴봅시다.
21.7.3 Subgroups

살려줘어어어ㅓ subring같은 subgroup입니다.
22.7.3(2) Cyclic group

최악 최흉의 간단한 group인 cyclic group에 대해 알아보겠습니다.
23.7.4 Group homomolphism and Isomolphism

Group에서의 Homomorphism과 Isomolphism에 대해 다룹니다.
24.7.5 Symmetric and alternating groups

벌써 현대대수 1학기 마지막 글입니다. 오늘은 Cayley's thm과 Symmetric and alternating groups에 대하여 다룹니다.