4.5 Irreducibility in Q[x]

JUHONGYEE·2022년 4월 20일

수학 현대대수

열심히 올리는 현대대수

목록 보기

12/24

서론

이번엔 f(x)가 Q[x]에 속해있다고 해보자. Q[x]는 계수, 즉 coeffcient를 유리수로 가지는 polynomial들의 집합이다.
여기서의 irreducibility를 따져보자.

우리는 f(x)가 언제 irreducibility인지 알고싶다!

Irreducibility in Q[x]

def of Primitive

f(x) in Z[x] is called primitive if gcd of all coefficients is 1.

정수 polynomial ring에서 가져온 polynomial에서 모든 coefficient의 gcd를 구했을 때 1이라면 primitive라고 한다.

Thm 4.21 Rational root test

Let f(x) = $a_nx^n+a_{n-1}x^{n-1}+...+a_0$ .
if f(r/s) = 0 for some nonzero r,s in Z with (r,s) =1, then $r|a_0$ and $s|a_n$

이건 우리가 고등학교 때 배운 내용이다. 좀 쉽게 내용을 적어보자.
어떤 기약분수 r/s가 있다. f(r/s)가 정수 다항식에서 해가 된다. 그러면 r이 상수항을 나누고 s가 n차항을 나눈다.

먼저 직관을 잡아보자.
만약 정수 polynomial이 아니라 유리수 polynomial이었다면, (x-r/s)g(x)로 쓸 수 있을 것이다.(g(x)는 정수polynomial로 가져오자. )얘는 다시 1/s(sx-r)g(x)로 쓸 수 있다. 이 때 (sx-r)g(x)만 가져와도 r/s가 해인 정수 polynomial이 된다. 얘는 당연히 최고차항에 s가 곱해질거니까 최고차항을 s로 나눌 수 있고 상수항에 r이 곱해지므로 상수항을 r로 나눌 수 있다.

ex) $(x-1/2)(x^2+1) = 1/2(2x-1)(x^2+1), (2x-1)(x^2+1) = 2x^3-x^2+2x-1$
최고차항은 2로 상수항은 1로 나누어 떨어진다.

proof)
$f(r/s) = a_n(r/s)^n+a_{n-1}(r/s)^{n-1}...+a_0 = 0$
왜냐면 r/s가 해이므로.
양변에 $s^n$ 을 곱해주자. 그러면 $a_nr^n+a_{n-1}r^{n-1}s...+a_0s^n = 0$

이 때,
1) $r|a_0$
$r(a_nr^{n-1}+a_{n-1}r^{n-2}s...+a_1s^{n-1}) = -a_0s^n$ 이므로 r이 $a_0$ 를 나누거나 $s^n$ 을 나누어야 하는데 s와 r은 gcd가 1이므로 $r|a_0$

2) $s|a_n$
$s(a_{n-1}r^{n-1}+a_{n-2}r^{n-2}s...+a_0s^{n-1}) = -a_nr^n$ 이므로 s가 $a_n$ 을 나누거나 $r^n$ 을 나누거나이다. 근데 또 gcd가 1이므로 $s|a_n$ .

Example) $f(x) = x^3-2x+3$ , r/s = +-1 or +-3. 직접 해보시라!
만약 해가 있다면 1,-1,3,-3 외에는 있을 수가 없다. 왜냐하면 만약 유리수가 해라면 분모가 최고차항을 나누고 분자가 상수항을 나누기 때문이다.

Gauss lemma

간단하게 요약하면 결국 유리수 근 즉, rational root가 존재한다면 polynomial이 두 정수 polynomial로 쪼걔질 수 있다라는 것이다. 만약 안 쪼걔지면 근이 없다는 뜻이다.

Lemma4.22 Primitivity

Let f(x),g(x),h(x) in Z[x]. f(x) = g(x)h(x). Let p be prime. if p|f(x), then p|g(x) or p|h(x).
<=> if g(x) and h(x) are primitive ,then so is f(x)

원래 lemma의 내용은 모든 p(prime)에 대해 f(x)를 나눈다면 g(x)나 h(x)를 p가 나누어야 한다는 내용이다. 모든 coefficient를 생각해볼까? p가 f(x)를 나눈다면 p는 모든 f(x)의 coefficient의 common divisor이다. 이 때 이 p가 g(x)나 h(x)를 나눈다는 것은 다시 그들의 모든 coefficient의 commondivisor라는 뜻이다.
그런데 이 친구의 대우를 생각해보자. 모든 p에 대해 g(x)와 h(x)를 p가 나누지 못하면 f(x)도 나누지 못한다. g(x)를 나누는 p가 없다는 것은 g(x)가 primitive라는 것이다. 만약 gcd가 1이 아니라면 다시 그 gcd가 prime factorization 될 것이기 때문이다. h(x)도 동일하게 primitive이다. 이 때 g(x)와 h(x)가 primitive라면 그 곱인 f(x) 또한 primitive가 된다는 내용이다.

proof)

$f(x) = a_nx^n+...+a_0$
$g(x) = b_mx^m+...+b_0$
$h(x) = c_kx^k+...+c_0$
라고 하자.

이때 $g(x)h(x) = b_0c_0+(c_0b_1+b_0c_1)x+(c_0b_2+c_1b_1+c_2b_0)x^2+...$

$Then a_0 = b_0c_0, a_1 = c_0b_1+c_1b_0, a_2 = c_0b_2+c_1b_1+c_2b_0, a_3...$
(여기서 조금 잘 생각해보면 $c_0$ 로 시작하지 않고 $c_1,c_2$ 이렇게 시작하고 $b_1,b_2$ 이렇게 끝날 수도 있는데 증명에는 문제가 없다.)

$a_j = b_0c_j+...+b_jc_0$

이 때 귀류법을 사용하여 contradiction을 이끌어내자.
p|f(x)이지만 p가 g(x)도 나누지 못하고 h(x)도 나누지 못한다고 가정하자.

p가 g(x)를 나누지 못하므로 g(x)의 coefficient를 작은 것부터 하나하나 p로 나누다보면 나누어지지 않는 것이 존재. 그 때의 index를 r이라고 하자.
h(x)도 마찬가지이므로 그 때의 index를 s라고 하자.

이 때 p|f(x)이므로, $p|a_{r+s}$ 이다.
그 때 $a_{r+s}$ 를 전개해보면 다음과 같다.

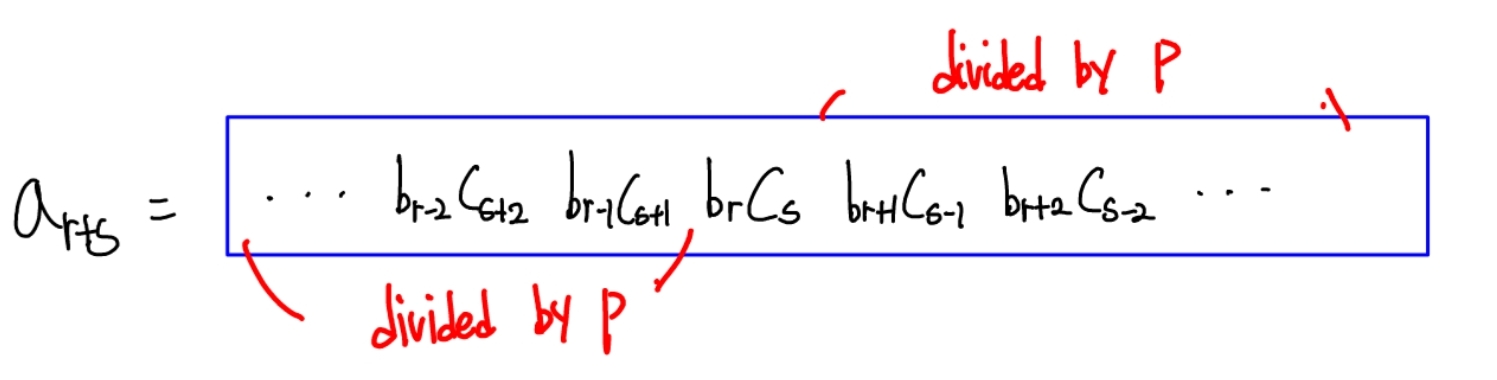
양 끝은 $a_0b_{r+s},a_{r+s}b_0$ 가 되는데 만약 $a_{r+s}$ 나 $b_{r+s}$ 가 없을 수 있지 않냐고 라고 얘기한다면 그냥 그 값이 0이라고 하면 된다. 왜냐하면 $1+x = 1+x+0*x_2+0*x_3$ 이나 마찬가지기 때문이다.
이 때 $b_rc_s$ 의 양 옆으로 뻗어나가있는 value들은 다 p로 나누어진다. 왜냐면 r,s가 p로 나누어지는 최소 index이기 때문이다. 예를들어 $b_{r-1},c_{r-1}$ 은 모두 p로 나누어 떨어진다.
하지만 $b_rc_s$ 는 p로 나누어떨어지지 않는다. 즉 $a_{r+s}$ 가 나누어 떨어지지 않는다. 즉, f(x)는 p로 나누어떨어지지 않는다. -> contradiction

증명 끝.

Thm 4.23 Irreducibility

Let f(x) be in Z[x]. Suppose f(x) = g(x)h(x) for some g(x),h(x) in Q[x]. Then there exist r,s in Q s.t f(x) = (rg(x))(sh(x)) and rg(x),sh(x) are in Z[x].
inverse도 성립(if and only if)

가우스는 진짜...레전드긴 하다...ㅋㅋㅋㅋ
그 의미를 그대로 써보면.

정수 polynomial f(x)가 deg = m과 deg = n의 유리수 polynomial로 인수분해 되면 deg = m과 deg = n의 정수 polynomial로도 인수분해 되고 deg = m과 deg = n 정수polynomial로 인수분해 되면 deg = m과 deg = n 유리수 polynomial로도 인수분해된다.

이건 대우가 쓸만한 명제이다. 대우 명제를 해석하면 이렇다.

f(x)가 deg = m과 deg = n 정수 polynomial로 인수분해가 되지 않는다면 deg = m과 deg = n 유리수 polynomial로도 인수분해되지 않는다.

증명은 한 방향만)
r,s를 Q에서 뽑을건데 rq(x)와 sh(x)가 primitive가 되게 뽑는다.(가능하다. 다 정수로 만들어주고 gcd로 나누어주면 된다.) 그러면 lemma4.2에 의해서 rg(X)sh(x)는 primitive이다. 즉 rsf(x)가 primitive이다. f(x)는 Z[x]의 원소이므로 rs = 1.(rs가 1이 아니면 coefficient들의 gcd가 1이 안나온다.)
즉 f(x) = rg(x)*sh(x).

ex) $x^4-5x^2+1$ 이 irreducible임을 보이기.
1) rationl root test로 degree가 1인 factor가 없음을 보이기
2) $(x^2+ax+b)(x^2+cx+d)$ 로 놓음으로 degree가 2인 factor가 없음을 보이기
즉 unit과 associate만 divisor.

Thm 4.24 Eisenstein's criterion

Let f(x) be in Z[X]. $f(x) = a_nx^n+a_{n-1}x^{n-1}+...+a_0$
Suppose there exist prime p satisfying the following conditions
1. $p|a_i$ for i = 0,1,2,...,n-1
2.p does not divide $a_n$
3. $p^2$ does not divide $a_0$
Then f(x) is irreducible in Q[x]