들어가는 말

벌써 현대대수 1학기 마지막 글입니다.
오늘은 Cayley's thm과 Symmetric and alternating groups에 대하여 다룹니다.
Cayley's thm은 처음에 group을 공부할 때 group의 본질은 무엇일까라는 질문의 답이 될 수 있습니다. group은 permutation group과 isomolphic하구나 라는 답을 얻게 되겠습니다.

마지막 현대대수1의 글, 7.5장을 시작해보겠습니다.

Thm7.21 Cayley's Thm

Any group G is isomolphic to a permutation group.

자 우리는 먼저 permutation group이 뭔지부터 알아보야 합니다. 그러면 symmetric group에 대해서 먼저 상기해야 한다는 것을 7.1 글을 보신 분들이라면 다 아실 겁니다.

symmetric group이란 먼저는 그 set을 함수들의 집합으로 가지고 있습니다. 이게 진짜 중요합니다. 함수들의 집합입니다. 그런데 그 함수들이 우리가 잘 알고 있는 permutation에 관한 함수들입니다.
그에 대해 우리는 symmetric group of T라는 용어를 사용하는데 T라는 set이 있을 때 이 set을 permutation 해주는 함수를 그 원소로 가지고 있다는 의미입니다. 무슨 의미인지 예시를 통해 봅시다.

T = {1,2,3}이라고 해봅시다. 이 때 symmetric group of T를 A(T)라고 씁니다. 그러면 이 symmetric group A(T)에는 무엇이 들어 있느냐, 바로 함수들이 들어 있는 것입니다.
그곳에는 6개의 함수가 존재하겠네요.

$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$,$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$,$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$

$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$,$\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}$,$\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$

예를 하나 들어보면 첫번째 함수를 $f_1$이라고 한다면 $f_1(1)$ = 1, $f_1(2)$ = 2, $f_1(3)$ = 3 와 같이 대응시키는 함수 $f_1$이 A(T)의 원소인 것입니다.

그렇게 6개의 함수 원소들이 있는 것이죠
여기서의 operation 즉, 연산은 composition 즉, 합성입니다. 함수의 합성이 연산인 것입니다. 우리는 이것이 group임을 보였습니다.

더 나아가 permutation group이라는 것은 무엇이냐. 이 6개의 원소 중 subset을 뽑아 group으로 만든 것을 permutation group이라고 한다는 것입니다.
물론 group의 조건을 잘 만족하는 subset이여야 합니다.

이런 상황에서 Cayley's thm은 우리에게 좋은 직관을 줍니다. 모든 group은 어떤 permutation group과 isomolphic하다, 즉 형태만 다른 것이지 본질이 permutation group에 있다 라는 것입니다.

저도 아직 정확한 직관을 얻지는 못한 것 같습니다만 그 위치를 바꾸는 것에 그 본질이 있는 것 같습니다. 한 번 증명해보며 확인해봅시다,

proof sketch)
먼저 지난 글에서 증명한 f:G→H 가 injective homomorphism이면 G≅Im(f)임을 상기해봅시다.

그를 생각하며 injective homomorphism f:G→A(G)를 찾아봅시다,

자 이 포인트에서 헷갈리면 안됩니다.
A(G)로 쓰이는 permutation group을 잡을건데 그 원소가(그 원소는 함수입니다.) 다음과 같게 할 겁니다.
For each a∈G, define $f_a : G→G$ by $f_a(x) = ax$ for x∈G. 만약 이 친구들이 permuatiton group A(G)에 속하고 injective이면 자연스럽게 Isomolphism을 찾을 수 있을겁니다.
다시 한 번 강조하면 permutation group의 원소들은 각각 함수입니다.

이때 아직 우리는 $f_a$가 permutation group의 원소인지 알지 못합니다. 한 번 확인해볼까요?
만약 $f_a$가 A(G)에 속한다면 $f_a$는 bijective function입니다.

Check 1. $f_a$ is injective.
Suppose $f_a(b)$=$f_a(c)$.
Then $ab = ac$ ⇒ $a^{-1}ab = a^{-1}ac$ ⇒ $b=c$.

∴ $f_a$ is injective

Check 2. $f_a$ is surjective.
suppose g∈G.
Then g = eg = $aa^{-1}g$ = $a(a^{-1}g)$ = $f_a(a^{-1}g)$

Since ∀g∈G ∃k∈G s.t f(k) = g, ∴ $f_a$ is surjective.

위의 Check들에 의해 $f_a$는 A(G)에 속한다고 할 수 있겠습니다.

자 그러면 $a$를 $f_a$로 보내는 함수가 surjective임은 확실한데 injective임도 보여야겠죠?
또한 homomorphism인지도 보여야 합니다. 그러면 Cayley의 정리가 완성이 됩니다.

Check 1. f is injective
Suppose $f_a = f_b$.
Then ∀x∈G $f_a(x)$ = $f_b(x)$ ⇒∀x∈G ax = bx ⇒ a=b(∵ There exist inverse of x)

Check 2. f is homomorphism
Suppose a,b ∈ G.
f(a)f(b) = $f_a∘f_b$ = a(b(x))= abx = f(ab)

$f_a$에서 연산은 composition입니다.
즉 homomorphism이군요.

Cayley의 정리가 결국 성립합니다.

group에서 operation의 과정은 결국 permutation에서는 위치를 바꾸어주는 작업과 동일하다는 직관을 우리는 습득할 수 있겠습니다.

7.5 Symmetric and alternating groups

The cycle notation

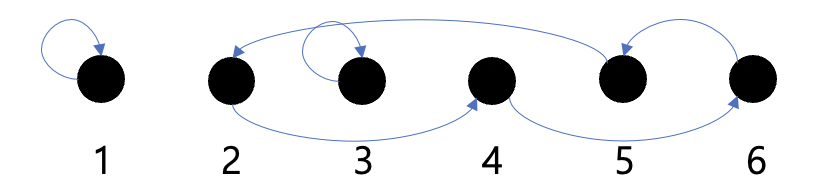
자자 G에 원소 1,2,3,4,5,6이 있다고 가정해봅시다. 한 permutation이 위와 같은 수의 변환을 만드는 함수라면 이걸 어떻게 표현할 수 있을까요? 보니까 1과 3 각각에서 2456에서 값들이 순환하고 있습니다. cycle이 있는 것이죠.

모든 걸 permutation을 다음에 나올 notation으로 표현할 수는 없지만 위의 예시는 최소 표현이 가능할 것 같습니다.

(2465) 라고 말입니다.
1과 3은 어차피 자기 자신으로 가기 때문에 쓰지 않고 순환하는 4개의 원소들을 적어준 것입니다. 2는 4로 4는 6으로 6은 5로 5는 다시 2로 가는 함수를 한 notation으로 표현이 가능한 것입니다.

(2456) = (4562) = (5624) = (6245) 라고도 할 수 있습니다. 그 관계만 잘 표현해준다면 장땡이죠.

예시를 두 개 더 봅시다.

Example

(153) = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 5 & 2 & 1 & 4 & 3\end{pmatrix}$

2와 4는 자기 자신으로 가기 때문에 그대로 두고 cycle이 있는 것들만 적어주는 것입니다.
$\space$

(23) = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 1 & 3 & 2 & 4 & 5\end{pmatrix}$
동일하게 1,4,5는 자기 자신으로 가기 때문에 그대로 둡니다.

이 때 (153)(23),(23)(153)을 고려해봅시다. 이는 함수의 composition입니다.

(153)(23) = (2153) 이 됩니다.
두 개를 좌우라고 표현하겠습니다.
(우)2를 넣으면 3이 나오고 (좌)3을 넣으면 1이 나오므로 21
(우)1을 넣으면 1이 나오고 (좌)1을 넣으면 5가 나오므로 215
(우)5를 넣으면 5가 나오고 (좌)5를 넣으면 3이 나오므로 2153
(우)3을 넣으면 2가 나오고 (좌)2를 넣으면 2가 나오므로 21532 = 2153

두 함수를 합성하니 이런 Cycle을 만들 수 있겠습니다.

commutative는 성립을 안해서 (23)(153)은 다른 답이 나옵니다. 직접 해보시면 좋겠습니다.

Remarks

1. Cycle notation에서는 원래 set의 총 개수 n의 정보가 없습니다. 그래서 같이 적어주어야 합니다.

2. 모든 1-cycle은 identity입니다. (1)=(2)=(3)...(n) = e. 그러므로 우리는 (1)을 identity로 써주겠습니다.

3. 모든 K-cycle은 order를 k로 가지고 있습니다.

처음엔 3번이 잘 이해가 안됐는데요
(567)을 세번 돌리면 (567) (756) (675) (567) 이렇게 해서 (567)로 돌아오게 되는 것이 아닌지 생각이 들었습니다. 그런데 $(567)^3$에 5를 대입해볼까요? 5를 넣으면 그 최종 값이 5가 나오게 됩니다. 6을 넣으면 6이 나오고, 7을 넣으면 7이 나오게 됩니다. 마지막 나오는 (567)은 결과입니다. 5자리에서 5가 나온다는 의미이죠. 그런 점에서 $(567)^3$은 identity일 수 밖에 없습니다.

$(567)^1$ = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 &6 &7\\ 1 & 2 & 3 & 4 & 6&7&5\end{pmatrix}$의 아랫부분만 계속 변해서

$(567)^2$ = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 &6 &7\\ 1 & 2 & 3 & 4 & 7&5&6\end{pmatrix}$

$(567)^3$ = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 &6 &7\\ 1 & 2 & 3 & 4 & 5&6&7\end{pmatrix}$

과 같이 합성한 친구들이 나오게 됩니다.

4. 모든 permutation을 cycle로 표현할 수는 없습니다.
   $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 &6\\ 2 & 1 & 4 & 6 & 5&3\end{pmatrix}$과 같은 permutation은 cycle이 2개가 들어있기에 한 notation으로 표현할 수는 없습니다.
   ((12)와 (346))

하지만 두 notation의 product로 표현할 수 있습니다. (12)와 (346)은 서로 cycle이 겹치지 않기 때문에 operation을 취했을 때 자연스럽게 위와 같은 permutation을 구할 수 있습니다.
(서로 겹치지 않는다는 성질을 disjoint라고 부릅니다.)

(12)(346)= (346)(12) 그리고 commtative도 성립을 하겠군요

(12)(346) = (346)(12) = $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 &6\\ 2 & 1 & 4 & 6 & 5&3\end{pmatrix}$

Obeservation 1.
그리고 우리는 증명하지는 않겠지만 Thm7.24로 모든 permutation을 disjoint한 두 permutation의 product로 표현할 수 있습니다.

Obeservation 2.
위의 예시에서 봤을 때 두 disjoint한 cycle은 위치를 바꾸어도 됩니다. 물론 증명은 생략하겠습니다.(Thm7.23)

Obeservation 3.
permutation의 order를 계산할 때는 permutation을 disjoint한 cycle들로 쪼걘다음 그들의 length의 lcm을 구하면 됩니다.(Thm7.25)

직관적으로 생각해볼 수 있는데 disjoint한 cycle들로 permutation을 쪼걜 수 있다면 그들은 각자 자신의 길이를 order로 갖습니다. 즉 identity로 만들기 위해서는 n제곱을 할 때 n이 그 길이의 최소공배수가 되면 되겠습니다.

예를 들어 (12)(346)에서는 (12)가 길이가 2고 (346)이 길이고 3이면서 disjoint이고 각각의 order가 2,3이므로 6번 operation해주면 identity가 되겠습니다. 직관적으로 당연하죠?

Alternating groups

Let $S_n$ be a symmetric group
1. A 2-cycle is called a transposition.
2. A permutation is called even(or odd) if it can be written as a product of even(or odd) number of transpositions.
3. The alternating group $A_n$ is the set of even permutations in $S_n$.

Example

$S_3$ = {(1),(12),(13),(23),(123),(132)}

(1) = (12)(12) = (13)(13) = (23)(23)
(123) = (23)(13)
(132) = (23)(12)

$A_3$ = {(1),(123),(132)}

그런데 정의만으로 우리는 어떤 permutation이 even number of transposition으로 쓰여질지 아닐지 알기가 쉽지 않습니다. 대신 우리는 $A_n$이 $S_n$의 subgroup이고 그 원소의 개수가 $n!\over 2$라는 것을 보이겠습니다.

3개의 step을 거칠건데요 그 과정은 다음과 같습니다.

Step1 (1)∈$S_n$ i not odd

Step2 No permutation is both even and odd.

Step3 $A_n$ has order $n!\over 2$

Let's start.
Step1 (1)∈$S_n$ i not odd
이게 제일 까다로운 과정인데요. 자세히 보셔야 합니다. 그래야 논리가 이해가 됩니다.

자 (1)이 $T_kT_{k-1}...T_1$과 같은 transposition의 product라고 해봅시다.
(순서가 반대인 이유는 오른쪽부터 연산을하기 때문입니다.)

자 transposition의 length는 2입니다.
Let $T_i$ = (cd) with c≠d∈{1,2,...,n}

위와 같은 condition은 일단은 transposition이기 때문이고 c=d가 같아버리면 identity가 되기 때문입니다.

그러면 $T_i$와 $T_{i+1}$에는 4가지 경우의 수의 관계가 있을 수 있습니다.

1. $T_{i+1}$ = (xy), cd와는 전혀 다른 두 수로 이루어진 transposition입니다.
   이 때 $T_{i+1}T_i$ = (xy)(cd) = (cd)(xy) = $T_iT_{i+1}$

즉, 두 위치를 바꿀 수 있습니다.(disjoint하기 때문이죠.)

2. $T_{i+1}$ = (xc), c하나는 같고 x는 d와 다릅니다.
   이 때 $T_{i+1}T_i$ = (xc)(cd) = (dxc) = (cd)(dx)

이번엔 (cd)의 위치를 옮겨버릴 수 있습니다. 대신 (xc)는 (dx)가 되었군요.
핵심은 (cd)를 옮길 수 있으면서 오른쪽에는 c가 남지 않는다는 겁니다.

3. $T_{i+1}$ = (xd), d 하나는 같고 c와 x는 다릅니다.
   2번과 비슷하겠죠?
   $T_{i+1}T_i$ = (xd)(cd) = (cxd) = (cd)(xd)
   여기도 (cd)를 옮길 수 있군요. 그리고 오른쪽에는 c가 안남습니다.

4. $T_{i+1}$ = (cd)
   Then $T_{i+1}T_i$ = (1)

똑같은 것 2개를 곱하면 자연스럽게 identity입니다.

우리는 위의 4가지 과정을 $T_{i+1}T_i$를 $T_i'T_{i+1}'$으로 바꾸는 과정이라 하겠습니다.
예를 들어 3번에서는 $T_{i+1}T_i$ = (xd)(cd), $T_i'T_{i+1}'$ = (cx)(xd)입니다.

우리는 (1) = $T_kT_{k-1}...T_1$이라고 가정했습니다. 그러면 어떤 j>1에 대해서는 $T_j=T_1$일 수 밖에 없습니다.
왤까요? 만약 아니라고 해봅시다. 위를 만족하는 j가 없는거죠. 그렇다면 (1) = $T_1T_kT_{k-1}...T_2$ 과 같이 쓸 수 있습니다. $T_1$을 우리는 1. 2. 3.경우에 깔끔하게 옮길 수 있기 때문이죠. 4. 과 같은 상황이 일어나지 않는다고 가정했으니까요.
그런데 이러면 모순입니다. 위의 1. 2. 3.을 자세히 볼까요? (cd)를 옮길 수 있으면서 오른쪽에는 c를 남기지 않습니다.즉, $T_kT_{k-1}...T_2$ 여기에는 c 항이 아예 없습니다.
그런데 우리는 (1) = $T_kT_{k-1}...T_1$이라고 했기 때문에 c가 한 번 나왔다면 최소 1개의 c는 더 있어야지 c를 c로 보내게 할 수 있습니다. (cd)에서 c를 d로 돌렸으면 다시 어떤 과정을 거쳐 c로 돌려버려야 하고 그러므로 $T_kT_{k-1}...T_2$에는 c가 최소한 하나는 있어야 합니다. 그런데 4. 과 같은 상황이 일어나지 않으면 c가 남지 않으므로 모순이죠.

그러므로 $T_1$은 어떤 것과 쌍으로 묶여 사라집니다. 다른 $T_k$들도 마찬가지입니다. 쌍으로 묶여 사라지죠. 그러므로 (1)은 even일 수 밖에 없습니다. ㅎㅎ 잘 생각해보세요.

Step2 No permutation is both even and odd.
Suppose $T_kT_{k-1}...T_1$ = $O_mO_{m-1}...O_1$, k는 짝수이고 m은 홀수입니다.
Then (1) = $(T_k)^{-1}(T_{k-1})^{-1}...(T_1)^{-1}O_mO_{m-1}...O_1$ = $T_kT_{k-1}...T_1O_mO_{m-1}...O_1$
(∵ transposition의 inverse는 자기 자신입니다.)

그런데 m+k는 odd이므로 step1에 의해 모순입니다.

그러므로 even이거나 odd이거나 입니다.

Step3 $A_n$ has order $n!\over 2$
$S_n$의 원소의 개수는 n!입니다. 그런데 그게 정확히 odd와 even으로 나뉘니 even만 모아 놓은 $A_n$의 원소의 개수는 $n!\over 2$일 수 밖에 없습니다.

---

드디어 끝났습니다. group에 대하여는 이제 시작한 것이나 마찬가지지만 1학기의 모든 내용을 정리하였습니다.
아는 내용을 남이 보기에 혹은 미래의 제가 읽기에 어떻게 하면 편할까를 고민하며 적었습니다.
방문자 수가 적어서 거의 미래의 저와 소통한다는 생각으로 적었던 것 같습니다 ㅎ
1학기 고생 많으셨습니다.

그리고 나도 고생 많았다!
앞으로 글을 읽고 있는 나는 왜 읽고 있는지 모르겠지만 목표를 이뤄서 나중에 수학을 들여다보고 있기를 바라. 이 1학기동안 블로그에 들였던 시간이 헛되지 않았으면 해.

고생했다.