✔️ROC curve

reference : https://angeloyeo.github.io/2020/08/05/ROC.html
-
FPR이 변할때 TPR이 어떻게 변하는지를 보여주는 곡선이다.(0~1 사이의 값을 가짐)
-
분류모델 성능 평가 시 반드시 기술해야할 사항은
모델의 정확도, 정밀도, 민감도(재현율)이 있다.
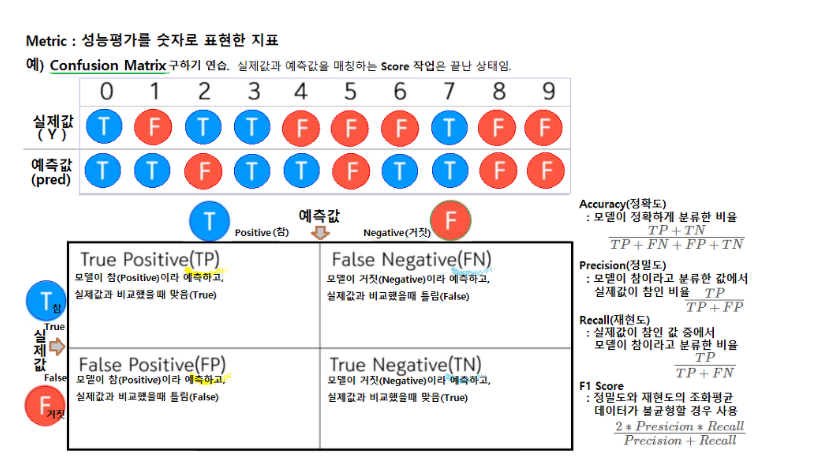
-
TP(True Positive) : 실제값과 예측치 모두 True
TN(True Negative) : 실제값과 예측치 모두 False
FP(False Positive) : 실제값은 False, 예측은 True
FN(False Negative) : 실제값은 True, 예측은 False
-
-
정확도(accuracy) :
TP + TN / TP + FN + FP + TN- P든 N이든 전체 예측 중에 맞춘 비율
-
재현도(Recall) :
TP / TP + FN- 실제 값이 Positive인 대상 중에 예측과 실제 값이 Positive로 일치한 데이터의 비율,
잘못 걸러내는 비율이 높더라도 놓치는 것이 없도록 하는 경우에 사용
- 실제 값이 Positive인 대상 중에 예측과 실제 값이 Positive로 일치한 데이터의 비율,
-
정밀도(Precision) :
TP / TP + FP- 예측을 Positive(1) 로 한 대상 중에 예측과 실제 값이 Positive(1)로 일치한 데이터의 비율
-
민감도(sensitivity) :
TP / TP + FN- 얼마나 우리가 예측하는 값을 빠뜨리지 않고 예측했는지를 나타내며, 실제로 Positive인 것들 중 얼마나 많이 맞추었는가를 의미
-
특이도(specificity) :
TN / FP + TN- 얼마나 0을 예측했는지. 0과 1 사이의 값을 가지며 1에 가까울수록 좋은 모델
-
조화평균(F1 Score) :
- 정확도와 정밀도를 이용해 구한다. (0.1)
- 정밀도와 재현율이 어느 한쪽으로 치우치지 않을 때 높은 값을 가짐
-
-
🔗 각 값에 대한 자세한 설명
🔗 참고
❗정밀도와 재현도 선택
- 모델이 나왔을때, 데이터의 성격을 보고 재현도(Recall)이 중요한지, 정밀도(Precision)가 중요한지 잘 판단해야 한다.
예제 : 50주년행사 경품 전화 / 우수고객 : 여행상품권
| 실제값/예측값 | 당첨 Positive | 낙첨 Nagative |
|---|---|---|
| 당첨 True | TP : 40 | FN : 5 (기회잃음) |
| 낙첨 False | FP : 15 (사기당함) | TN : 40 |
accuracy : 80/100 = 80%
정밀도(Precision) : TP / TP + FP ... 40 / 55 = 72%
재현도(Recall) : TP / TP + FN ... 40 / 45 = 88%
이 예제의 경우에는 경품에 당첨되지 않았는데도 당첨 메시지가 고객에게 전달되는 경우인
정밀도의 상황(사기당함)이 더 중요하다.
✏️ROC curve 예제
make_classification 함수로 임의의 샘플 데이터를 생성했다.
#샘플100 / 독립변수2 생성
x,y = make_classification(n_samples=100, n_features=2, n_redundant=0, random_state=123)
model = LogisticRegression().fit(x,y)
y_hat = model.predict(x) #예측값
#결정/판별함수 - 판별 경계선 설정용
f_value = model.decision_function(x)
#판별,예측,실제값
df = pd.DataFrame(np.vstack([f_value,y_hat,y]).T,columns=['f','y_hat','y'])
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y, y_hat))
#[[44 4]
# [ 8 44]]confusion_matrix 를 확인하여 정밀도, 재현도, 특이도를 수식으로 계산해보았다.
# accuracy TP + TN / 전체수
acc = (44+44)/100
# 재현도(Recall) TP / TP + FN
recall = 44 / (44+4)
# 정밀도(Precision) : TP / TP + FP
precision = 44 / (44 + 8)
# 특이도 TN / FP + TN
specificity = 44 / (44 + 8)
#위양성률
fallout = 8 / (8+44) #또는 1-특이도 (1-specificity)
accuracy : 0.88
재현도(Recall) : 0.916
정밀도(Precistion) : 0.84
특이도 : 0.84
위양성률 : 0.153위양성률은 1-특이도 로도 계산 할 수 있다.
from sklearn import metrics 을 사용하여 정밀정확도 점수와 보고서 함수로 한번에 출력해보자
from sklearn import metrics
ac_score = metrics.accuracy_score(y, y_hat)
print(ac_score) #0.88
cl_report = metrics.classification_report(y, y_hat)
print(cl_report) precision recall f1-score support
0 0.85 0.92 0.88 48
1 0.92 0.85 0.88 52
accuracy 0.88 100
macro avg 0.88 0.88 0.88 100
weighted avg 0.88 0.88 0.88 100
fpr, tpr, threshold = metrics.roc_curve(y,model.decision_function(x))
- threshold : 임계값
- TPR은 1에, FPR은 0에 가까울수록 좋다.
이제 이 결과로 ROC curve를 그려보자
#ROC 커브
plt.plot(fpr,tpr,'o-',label="Logistic Regression")
plt.plot([0,1],[0,1],'k--',label='classifier line(AUC:0.5)')
plt.plot([fallout],[recall],'ro',ms=10)
plt.xlabel('fpr')
plt.ylabel('tpr')
plt.legend()
plt.show()
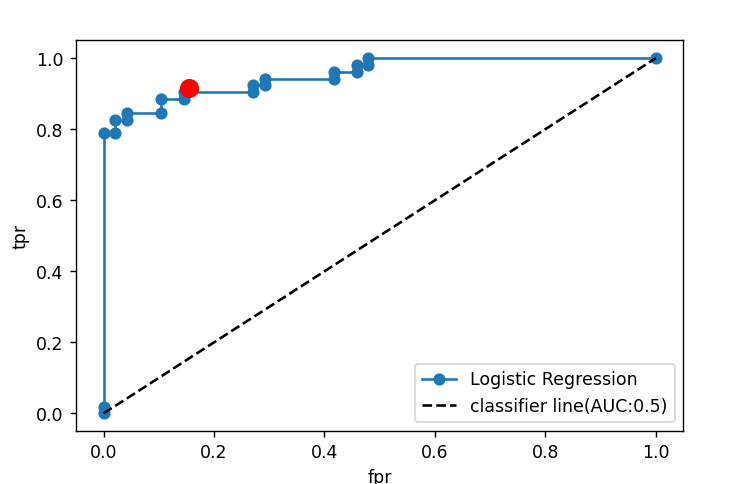
- AUC(Area Under the Curve)
ROC 커브 하단 영역의 넓이를 구한 값으로, 0-1사이의 값을 갖는다
더 높을수록 더 좋은 분류 성능을 의미한다.
print('AUC : ', metrics.auc(fpr,tpr)) #0.968