
📌 사용 환경
Python 3.10.2
conda 24.9.0
JupyterLab 4.2.5
어제 갑작스럽게 velog의 서버가 터져서 하루 미뤄진 점에 대한 양해를 구하며 🙏
Pandas를 이용해서 DDA, Seaborn을 이용해서 EDA를 했다.
그렇다면 다음은 확증적 데이터 분석 CDA(Confirmatory Data Analysis), 검증이다.
먼저 통계에 대한 개념을 다시 잡고가자.
통계란 다양한 데이터를 이용해 현상을 파악하고 분석하여 미래로 이어주는 것으로
수능시험에서 이용하는 표준점수, 시험 평균 점수, 강수량 등이 있다.
보통 자연과학, 사회과학 등 많이 쓰인다.
그렇다면 이런 통계를 구하는데, 어떤 데이터를 기준으로 할까?
1. 모집단(population)과 표본(sample)
크게 모집단(population)과 표본(sample)이 있다.
모집단(population)은 전체 데이터를 말하는데, "모을 수가 없다"라고 이해하면 된다.
우리나라 20대 평균 연봉을 구하고 싶다면, 우리나라 20대 전체가 모집단이다.
그런데 모두를 조사하는 것은? 당연히 불가능하다. 모집단을 다 모을 수 없다.
그래서 표본(sample)이라는 것이 있다.
모집단에서 일부만 뽑아낸 부분 데이터이며, 이런 표본을 뽑는 과정을 표집(sampling)이라고 한다.
이 샘플링을 잘해야 한다. 즉 유의미한 데이터를 뽑아내야 한다.
그렇다면 모집단에서 표집(sampling)을 할때, 뽑을 개수를 정해야하는데 이를 표집수(N)라고 한다.
예를들어 N=100이라면, 샘플(sample)이 100개, 즉 행이 100개 이렇게 이해하면 된다.
그리고 표집(sample)에는 종류가 많은데, 그 중 머신러닝에서 많이 쓰는 무선표집(Random Sampling)이라는 것이 있다.
무선표집이란 sampling시 어떤 기준을 두지 않고 무작위로 추출하는 과정이다.
만약 주관적으로 정해서 뽑는다면 편향(치우친)된 데이터를 뽑을 수 있고 좋지 않다.
따라서 머신러닝에서는 랜덤하게 뽑는다.
2. 통계
2.1. 기술통계
기술 통계는 데이터를 요약하고 설명하는 데 사용되는 통계적 방법으로 데이터의 간결한 요약 정보를 제공한다.
예를들어 평균이나, 분산, 표준편차, 그리고 histplot이나 boxplot 등으로 데이터를 시각화하고 요약하는 것들을 말한다.
2.2. 추론통계
추론통계는 먼저 추정과 검정(검증)으로 나눈다.
표본(sample) 데이터를 이용해 모집단(population)에 대한 추정을 하고, 가설을 검정하는데 사용한다.
예를들면 sample 데이터의 평균이나 분산을 이용해 모집단의 평균이나 분산을 추정하거나, 두 그룹의 차이가 있는지 확인하는 가설 검정 등을 말한다.
모집단은 컴퓨터에서 계산하는 것이기 때문에 머신러닝에서는 모을 수 있다.
그런데 통계는? 컴퓨터로 계산을 못하니까 표본을 이용해서 해야한다.
그렇다면 추론통계는 언제 사용될까? 바로 파라미터를 설정할때 들어간다.
간단하게 예를들면 다음과 같다.
def plus(x,y):
p=x+y
print(p)
plus(1,2)이런 함수가 있다고 했을때, 이를 실행하면 그냥 3이 나오고 끝이었다.
그런데 만약 print(p)의 값이 10이라고 정해져있다면?
10이 되기위해서 어떤 값을 전달해야할까?
(2,8), (5,5)와 같은 값들이 있을 것이다.
이렇게 10이라는 결과값에 맞춰서 x와 y값을 추정하는 것이다.
이게 사실 이미 만들어져 있다.
지금 만든 plus(x,y) 함수는 사실 너무 간단한 함수여서 명확하게 알 수 있는데, 사실은 그 함수안에 굉장히 복잡하다.
따라서 지금처럼 (1,9), (2.8)등을 쓰면 10을 퍼펙트하게 맞출 수 있지만,
만약 x+y라는 수학적 공식을, 즉 내부를 잘 모른다면?
(1,2)와 같은 값들을 던질 수도 있는 것이고, 그러면 0.2라는 예측율이 나오는 것이다.
즉 이렇게 추정은 파라미터를 찾는 것이다.
이 내용들이 통계, 즉 수학의 부분이다.
정통통계는 표본을 가지고 모집단을 추론하는 것인데,
머신러닝은 표본이 데이터가 되는 거고, 파라미터를 추정하는 것이다.
그리고 검증은 나중에 예측변수 y의 값을 알기 위해 x1~x100까의 변수가 있다면 거기서 필요한 변수만 골라서 쓰기위해 사용한다.
하지만 내부로 들어가면 추정하는 과정은 똑같다.
그리고 수학적인 부분은 함수가 알아서 해주기때문에 다루지 않지만 예를들어 최소제곱법과 같은 부분은 머신러닝에서 사용되기 때문에 이런 몇개는 나중에 머신러닝 부분에서 진행할 예정이다.
추론통계에서는 주로 가설검정을 많이 다룬다.
이제 추정과 검정에 대해 나눠서 정리할 예정인데 정리 전에 아래 내용을 보면 조금 도움이 될 것이다.
추정은 예를들면 100명의 20대 연봉 샘플을 뽑아서 그들의 평균 연봉이 2600만 원이라면, 모집단(전체 20대)의 평균 연봉을 2600만 원으로 추정하는 과정이다.
그리고 검정은 "우리나라 20대의 평균 연봉이 2500만 원이다"라는 가설을 세우고, 그에 대해 100명의 샘플에서 나온 평균 연봉이 2600만 원이라면, 이 샘플이 2500만 원이라는 귀무가설을 기각할 수 있는지 검정하는 과정이다.
이렇게 알아두고 이제 각각 알아보자.
2.2.1. 추정
통계학에서는 모집단은 절대 안된다. 뽑을 수가 없다.
그러니 무조건 샘플을 뽑는다. 즉 모든 통계는 sample이 기준이다.
sample을 100개를 모았다면(N=100) 그 sample에서 평균, 분산, 표준편차을 구할 수 있다.
그러나 모집단은 구할 수 없다. 데이터가 없기 때문에 알 수 없다.
따라서 표본의 평균, 분산, 표준편차를 이용해서 모집단의 모수의 값인 평균, 분산, 표준편차를 추정하는 것이다.
다시 말하면, 모집단의 평균을 구하고 싶은데, 우리나라 20대의 평균 연봉을 알고 싶지만, 20대 전체를 다 조사할 수 는 없다.
따라서 100명의 20대 sample을 뽑아서 그들의 평균 연봉을 구한다.
그리고 이 표본에서 나온 평균 연봉은 모집단(전체 20대)의 평균 연봉을 추정하는 값이 된다.
즉 추정은 모집단의 값을 알아내기 위해 표본에서 얻은 값을 기반으로 추정하는 과정을 말하는 것이다.
그리고 이런 추정의 종류에는 점 추정과 구간추정의 2가지가 있다.
점 추정이란 모집단의 파라미터를 하나의 값으로 추정하는 방법이다.
예를들면 표본의 평균을 사용하여 모집단 평균을 추정하는 것이다.
그리고 이렇게 값이 하나가 나오는 것을 점 추정이라고 한다.
그리고 구간 추정이란 모집단의 파라미터가 특정 구간에 있을 것이라고 추정하는 방법으로, 추정 값에 대한 신뢰도를 나타낸다.
예를들면 모집단의 평균은 2500만원에서 3000만원 사이일 것이라고 구간을 추정하는 것이다.
그런데 이 각 점(값)이나 구간을 추정해 내는 부분은 수학적인 부분이다.
점 추정은 표본의 평균이나, 분산, 중위수, 최빈수 등에 적률법, 최대가능도 추정법(최대우도법), 최소제곱법 등을 적용하여 모집단의 각 값들을 내는 것이고,
구간 추정은 신뢰도, 신뢰구간을 이용한다.
그래서 머신러닝으로 가서 예측 값의 신뢰도를 평가하거나, 비지도 학습, 이상치 탐지 등을 할때 사용되므로 후에 다룰 예정이다.
따라서 지금은 모집단의 평균과 분산, 표준편차를 구하는 수학적인 내용에 대해서만 조금 알면 된다.
(이 부분은 통계 수학을 작성했던 글에서 추가해서 다룰 예정)
2.2.2. 검정
검정은 모집단에 대해 어떤 주장을 검증하는 과정을 말한다.
sample 데이터로 부터 모집단의 특정한 모수의 값이나 확률분포에 대하여 어떤 가설을 설정하고 하고 이 가설이 성립하는지를 결정하는 것인데, 여기서 가장 중요한 개념인 가설에 주목해야한다.
이 가설을 하나 새워두고, 주어진 가설이 사실인지 아닌지를 확인하는 것이 주된 내용이다.
(참고로 모수는 모집단의 평균, 분산, 비율, 표준편차 등 통계적인 특성치를 말한다. 또 샘플데이터에서 모집단으로의 검정에 대한 부분이 주가 된다.)
먼저 이 가설에는 귀무가설과 대립가설이 있다.
귀무 가설(H₀) 이란 차이가 없다거나 변화가 없다는 가설이다.
대립 가설(H₁) 이란 차이가 있거나 변화가 있다는 가설이다.
주어진 가설이 맞다고 믿고, 이를 확인하기 위해 표본을 분석하여 통계적으로 유의미한 차이가 있는지를 검토하는데, 예를들면 다음과 같다.
귀무가설을 모집단에 대해서 "우리나라 20대의 평균 연봉은 2500만원이다." 라고 세웠다.
그런다음 20대의 샘플을 100명 정도 뽑아서 그 표본의 평균 연봉을 구한다.
예를 들어 표본에서 평균 연봉이 2600만원 이라고 나왔다면, 이것이 귀무가설과 일치하는지를 확인해야 하는 것이다.
반대로 대립가설은 "우리나라 20대의 평균 연봉은 2500만원이 아니다."라는 가설이다.
그래서 뽑은 샘플의 평균이 2500만원과 통계적으로 큰 차이가 나는지를 검증한다.
만약 이때 차이가 없다고 판단되면 귀무가설을 채택하고, 차이가 있다고 판단되면 귀무가설을 기각한다.
즉 검정은 주어진 가설이 참인지 거짓인지를 표본을 통해 확인하는 과정이다.
그런데 여기서 이 통계적으로 차이가 나는지를 알아야 한다고 했는데, 이 차이를 알기위해 p-value와 유의 수준(α, 0.05)이 사용된다.
p-value는 확률값으로 0~1사이의 값이며, 유의수준은 0.05로 정해져 가설검정의 판단 기준이 된다.
그리고 이 두 값을 비교하여 가설의 참과 거짓을 판단하는데, 이전 상관분석에서 다뤘던 corr()함수를 통해 상관계수와 0.5를 비교했던 부분과 비슷하다.
p-value > 0.05인 경우에는 귀무가설을 채택하고
p-value < 0.05인 경우에는 귀무가설을 기각한다.
(p-value를 구하는 과정은 따로 다루지 않겠다.)
또 귀무가설과 대립가설은 차이가 있는데 다음과 같다.
- 귀무가설: 보통 상태, 일반적인 상태, 평균의 차이가 없음, 상관성이 없음, 연관이 없이 독립적, 분산의 차이가 없음
- 대립가설: 의심하는 상태, 규명하는 바, 일반적이지 않은 이상상태, 평균의 차이가 있음, 상관성이 있음, 연관이 있으며, 분산의 차이가 있음
3. 확증적 데이터 분석(CDA) : 통계적 가설 검정 기법
통계적 가설 검증 기법 (표본 -> 모집단 추론(추정과 검정))
- 귀무가설(H₀): 보통 가설, 일반적인 상태(지구는 둥글다.)
- 대립가설(H₁): 규명하고자 하는 가설(지구는 네모나다.)
- p-value (확률값)를 통해서 가설이 참/거짓 인지 확인하는 분
- 유의 수준: 가설 검정 판단의 기준 0.05
- p-value > 0.05: 귀무 가설 참 (귀무 가설 기각 실패)
- p-value < 0.05: 대립 가설 참 (귀무 가설 기각)
- 유의 수준: 가설 검정 판단의 기준 0.05
규명하고자 하는 바를 가설로 수립하고, 해당 가설이 참인지 거짓인지를 객관적 수치(p-value)로 규명하는 분석기법이다.
검정을 할때는 먼저 크게 단일변수와 다변수의 경우로 나눈다.
이전 EDA, 시각화 부분에서도 나눠서 진행했듯이 이 CDA도 다르다.
즉 단일 변수 검정과 다변수 검정을 다 다루고 나면,
DDA로 데이터의 구조를 확인하고, EDA로 시각화를 하고 CDA로 가설검정을 하는 순서인 것이다.
3.1. 단일 변수 검정
연속형: 정규성 검증, One Sample T-Test(1 표본 평균 검증)
범주형: 비율 검증
단일 변수검정에는 연속형과 범주형 둘로 나누며,
연속형에는 정규성 검증과, One Sample T-Test가 있고,
범주형에는 비율 검증이 있다.
이전 글에서 위키독스에서 연습한 Tips 데이터셋을 이용한다.
tips=sns.load_dataset("tips")
tips.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 244 entries, 0 to 243
Data columns (total 7 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 total_bill 244 non-null float64
1 tip 244 non-null float64
2 sex 244 non-null category
3 smoker 244 non-null category
4 day 244 non-null category
5 time 244 non-null category
6 size 244 non-null int64
dtypes: category(4), float64(2), int64(1)
memory usage: 7.4 KB3.1.1. 연속형(숫자형) 검정
정규성 검정
One Sample T Test(1 표본 평균 검정)
3.1.1.1. 정규성 검정
정규성 검정을 해보자.
정규성 검정이란, 정규 분포인지 아닌지를 따지는 것이다.
먼저 total_bill의 그래프를 보자. 단일변수, 연속형의 시각화(EDA)는? histplot을 이용한다.
sns.histplot(data=tips, x="total_bill", kde=True)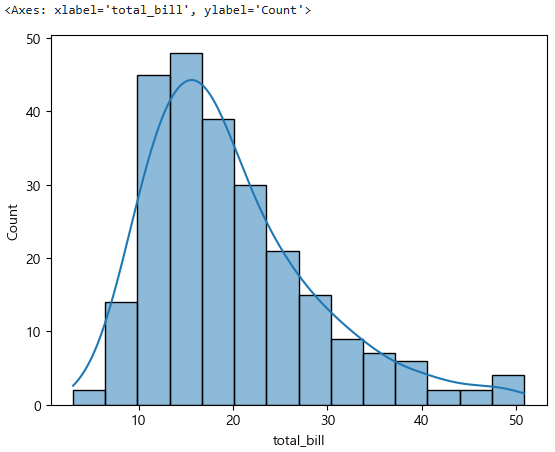
이렇게 식사요금의 분포를 그려서 보니까 이게 정규분포인지 아닌지 모르겠고, 결국 최종적인 목표인 모집단일때는 정규분포일까를 알아야 한다.
따라서 이를 먼저 샘플데이터로 보고 정규성 검증을 해보자.
(샘플데이터가 정규분포여도 모집단으로 가면 다를 수 있으니까)
정규 분포인가? (평균으로부터 적당히 잘 퍼져있는가?)
- 귀무가설: 해당 연속형(식사요금) 데이터 분포는 정규분포이다. -> 일반적인 통계적 가설 / p-value < 0.05 유의수준
- 대립가설: 해당 연속형(식사요금) 데이터 분포는 정규분포가 아니다. (비정규분포) -> 우리의 가설 / p-value > 0.05 유의수준
- 기준
- 유의수준(α) 0.05
- p-value
이 정규성 검정을 위해서는 normaltest()라는 함수를 사용한다.
이 함수안에 정규성 분포를 계산하는 통계적인 부분이 다 들어있다.
(p-value가 나온다.)
stats.normaltest(tips["total_bill"]) NormaltestResult(statistic=45.11781912347332, pvalue=1.5951078766352608e-10)여기서 보면 pvalue=1.5951078766352608e-10 이렇게 나와 있는데, 이 마지막에 있는 -10에 주목해야한다.
이는 앞에 0이 10개가 있다는 뜻이고, 1.59 × 10-10을 말하며 즉 pvalue = 0.00...159 이 된다.
즉 0.000...15 > 0.05 이므로, 대립가설이 참, 귀무가설은 기각, 따라서 식사 요금 연속형 데이터는 비정규분포임을 말한다.
또 tip에 관해서 보면 다음과 같다.
sns.histplot(data=tips, x="tip", kde=True)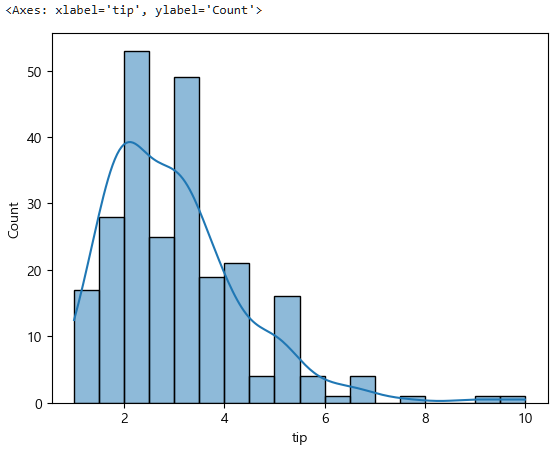
이는 딱봐도 정규분포가 아니긴한데, 우선 정규성 검정을 해보면,
stats.normaltest(tips["tip"]) NormaltestResult(statistic=79.37862574074785, pvalue=5.796294322907102e-18)이 또한 -18이니까 0이 앞에 18개가 붙는다.
따라서 0.00...579 < 0.05 -> 대립가설 참, 귀무가설 거짓, 정규분포가 아니다.
size도 마찬가지다.
sns.histplot(data=tips, x="size", kde=True)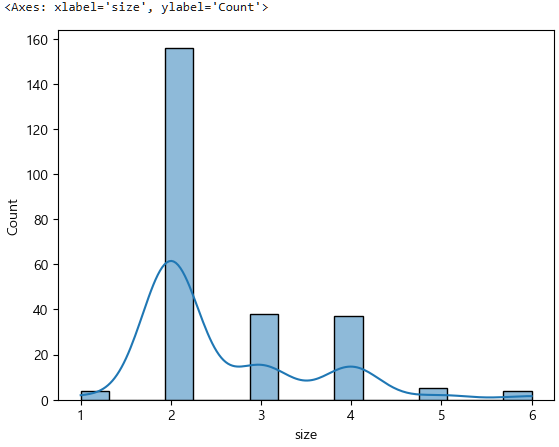
stats.normaltest(tips["size"])NormaltestResult(statistic=64.55815532237287, pvalue=9.580202540024401e-15)0.00..958 < 0.05 -> 대립가설 참, 귀무가설 거짓, 정규분포가 아니다.
3.1.1.2. One Sample T-Test(1 표본 평균 검정)
하나의 값과 하나의 집단 간의 평균 검정
- 귀무가설: A값과 집단의 평균이 같다.(평균의 차이가 없다.)
- 대립가설: A값과 집단의 평균이 다르다.(평균의 차이가 있다.)
One Sample T-Test는 하나의 값과 하나의 집단 간의 평균 검정을 하는데,
이는 앞서 귀무가설과 대립가설의 차이에 대해 말한 부분을 다시 봐야한다.
또 귀무가설과 대립가설은 차이가 있는데 다음과 같다.
- 귀무가설: 보통 상태, 일반적인 상태, 평균의 차이가 없음, 상관성이 없음, 연관이 없이 독립적, 분산의 차이가 없음
- 대립가설: 의심하는 상태, 규명하는 바, 일반적이지 않은 이상상태, 평균의 차이가 있음, 상관성이 있음, 연관이 있으며, 분산의 차이가 있음
여기 귀무가설에서 보통상태, 일반적인 상태까지는 정규성 검정을 했는데,
그 다음인 평균은 이 One Sample T-Test, 1 표본 평균 검정부분이다.
그렇다면 성별 tip의 평균을 기준으로 잡아보자.
tips["sex"].value_counts()sex
Male 157
Female 87
Name: count, dtype: int64남녀 전체의 tip의 평균을 보면
tips["tip"].mean()2.99827868852459이제 groupby를 사용해서 성별 팁의 평균을 보는 것이다.
tips.groupby("sex", observed=False)["tip"].mean() # 카테고리형이니까 observed=Falsesex
Male 3.089618
Female 2.833448
Name: tip, dtype: float64그러면 남녀 전체로 보면 평균 팁으로 2.99달러를 주는데,
남자와 여자가 평균인 2.99하고 차이가 있는가를 보면, 차이가 있긴한데, 매우 작은 차이다.
그런데 만약 이게 모집단으로 간다면, 데이터가 엄청 많을 것인데 0.1정도면 차이가 있을까? 이걸 보는 것이다.
tips_m=tips[tips["sex"]=="Male"]
tips_f=tips[tips["sex"]=="Female"]
tips_m.shape, tips_f.shape((157, 7), (87, 7))이제 하나의 값(tip 평균)과 하나의 집단(남 or 녀) 간의 평균을 검정해보자.
먼저 남자 집단이다.
stats.ttest_1samp(tips_m["tip"], tips["tip"].mean()) # 3.08과 2.99 비교TtestResult(statistic=0.7685681440821323, pvalue=0.44331167428061835, df=156)pvalue 0.44 > 0.05 유의수준 이므로 귀무가설이 참, 귀무가설 기각실패, 평균의 차이가 없다.
이제 여자 집단이다.
stats.ttest_1samp(tips_m["tip"], tips["tip"].mean()) # 3.08과 2.99 비교TtestResult(statistic=-1.3259534498746917, pvalue=0.18836618104053912, df=86)pvalue 0.18 > 0.05 유의수준 이므로 귀무가설이 참, 귀무가설 기각실패, 평균의 차이가 없다.
이렇게 보니 좀 더 정리가 될 것이다.
표본을 모집단은 어떨것이라는 가설을 검증하는 것이다.
3.1.2. 범주형(문자형) 검정
3.1.2.1. 비율 검정
One-Proportions Z-Test, 1 표본 비율 검정
- 특정 모집단의 비율이 기대값(기준값)과 다른지 검정
- 귀무가설(H0): 표본 비율과 기준 비율의 차이가 없다.
이 비율 검정은 보통 만족도를 조사할때 사용하기 때문에 이번에는 부산시 업무관계자 만족도 조사 공공데이터를 이용한다.
링크: https://data.busan.go.kr/bdip/opendata/detail.do?publicdatapk=15042279
먼저 데이터를 읽어와서 구조를 보자.
busan_servey_df=pd.read_csv("./data/pandas/Busan_Servey.csv", encoding="cp949")
busan_servey_df.shape(60, 4)busan_servey_df.head()
busan_servey_df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 60 entries, 0 to 59
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 업무명 60 non-null object
1 조사일자 60 non-null object
2 조사매체 60 non-null object
3 점수 60 non-null float64
dtypes: float64(1), object(3)
memory usage: 2.0+ KB이제 비율검정을 해야하기 때문에 object형인 점수를 살펴보자.
busan_servey_df.describe()count 60.000000
mean 98.500000
std 6.247033
min 60.000000
25% 100.000000
50% 100.000000
75% 100.000000
max 100.000000
Name: 점수, dtype: float64점수를 봤는데 점수가 너무 높다.
그래서 먼저 100점인 애들만 따로 뽑아보자.
score=busan_servey_df[busan_servey_df["점수"] == 100]
score.shape(55, 4)그랬더니 55명이 뽑혔다. 전체는 60명.
그렇다면 이제 전체 샘플 수와 100점으로 응답한 수를 비교해야한다.
그리고 그 기준 비율을 정해야하는데,
지금보면 점수가 굉장히 높기 때문에 0.9정도로 설정했다.
count=score["점수"].count()
nobs=busan_servey_df["점수"].count()
prop=0.9 # proportion
print(count, nobs, prop)55 60 0.9- 귀무가설: 표본비율과 기준비율의 차이가 없다.
- 대립가설: 표본비율과 기준비율의 차이가 있다.
먼저 ztest를 위해 라이브러리를 import해주자.
from statsmodels.stats.proportion import proportions_ztest이제 ztest를 진행하면,
proportions_ztest(count, total, proportion)(0.467099366496912, 0.6404287874127922)이를 보면 p-value가 0.64가 나온 것을 알 수 있다.
따라서 0.64 > 0.05 이므로, 비율의 차이가 없고, 귀무가설이 참이고, 귀무가설 기각이 실패한 것이다.
즉, 90% 이상이 만족했다는 것이다.
2 표본 비율 검정 (Two-Proportions Z-Test)
- A그룹 100명 중 60명 특정(만족도 9점) 설문에 응답하고 B그룹은 120명 중 특정(만족도 9점) 설문에 응답
- 비율에 차이가 있는지
- 귀무가설: 비율에 차이가 없다.
- 대립가설: 비율에 차이가 있다.
사실이 비율검정은 머신러닝에서 많이 사용하지 않기 떄문에
2 표본 비율 검정 (Two-Proportions Z-Test)에 대해서는 간단하게 다룬다.
groupA=100
answer_groupA=60
groupB=120
answer_groupB=70
counts=[answer_groupA, answer_groupB]
nobs=[groupA, groupB]
proportions_ztest(counts, nobs)(0.25035587206626936, 0.8023121521186127)p-value는 0.8이므로 귀무가설은 참이고, 귀무가설은 기각됐으며, 설문 만족도 (비율)에 차이가 없다.
3.2. 다 변수 검정
x범주형(문자) y연속형(숫자): 두 집단간의 차이
x범주형(문자) y범주형(문자): 연관분석 (성별에 따라서 합격 여부가 차이가 있는가) -> Chi Square Test, 비지도학습에서 할 예정
x연속형(숫자) y연속형(숫자): 상관분석 -> 했음 (정규성 검증은 따로 안했는데, corr함수에 다 들어가 있음) -> 회귀 예측 모델에서 더 할 예정
x연속형(숫자) y범주형(문자): 분류 예측 모델 -> 머신러닝에서 할 예정
그렇다면 지금까지 하나의 컬럼(단일변수)으로 정규성 검정과 1샘플 이런걸 왜했을까?
지금부터 할 다변수 검정을 할때, y값이 정규인지, 비정규인지에 따라 진행하는 방향이 다르기 때문이다.
3.2.1. x범주형(문자) y연속형(숫자) - 두 집단간의 차이
성별, 흡연여부, 식사 타임, 요일에 따른 팁 차이
먼저 y(팁), 연속형이 정규성이 있는지(정규분포인지, 비정규분포인지) 확인해야한다.
그런데 앞서 봤듯이 팁에 정규성이 하나도 없었다.
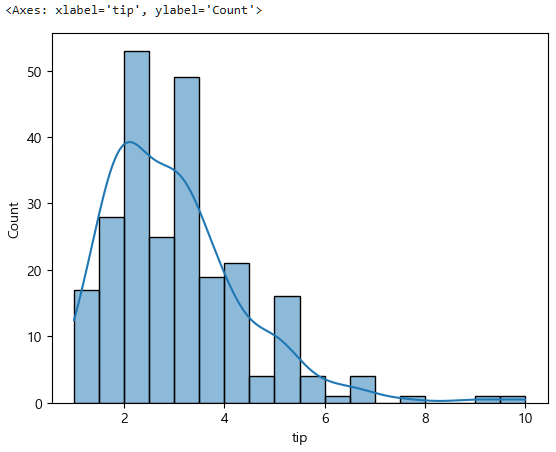
식사요금, 팁, 인원수 모두 비정규, 대립가설이 맞았었다.
어찌됐든 x범주형 y연속형의 검정은 y의 정규성을 먼저 판단하고나서 거기서부터 갈린다.
순서는 다음과 같다.
- 정규성검정 (stats.normaltest())
- 정규형 -> 등분산 검정: Levene Test (stats.levene())
1.1. 등분산 -> x항목의 수
- 2집단: T-Test (stats.ttest_ind( , equal_var=True))
- 3집단 이상: ANOVA Test (stats.f_oneway())
1.2. 이분산 -> x항목의 수
- 2집단: T-Test (stats.ttest_ind( , equal_var=False))
- 3집단 이상: Kruskal Wallis Test (stats.kruskal())- 비정규형 -> x항목의 수
- 2집단: Wilcoxon Test (stats.ranksums())
- 3집단 이상: Kruskal Wallis Test (stats.kruskal())
(여기서 T-Test는 One Sample T-Test가 아닌 Two Sample T-Test다)
즉, y가 정규형일때 등분산인지, 이분산인지
그리고 또, 등분산일때 x 항목에 수에 따라 2집단일때와 3집단 이상일때
이분산일때 x 항목의 수에 따라 2집단일때와 3집단 이상일때로 나뉜다.
y가 비정규형일때는 바로 2집단일때와 3집단 이상일때로 나뉜다.
3.2.1.1. 비정규성
먼저 y가 비정규일때를 보자.
- 성별에 따른 팁차이
tips.groupby("sex", observed=False)["tip"].mean()sex
Male 3.089618
Female 2.833448
Name: tip, dtype: float64위에서는 전체평균과의 차이를 물어봤는데, 이는 두 집단의 차이가 있는지를 확인하는 것이다.
sns.barplot(data=tips,x="sex",y="tip",errorbar=None)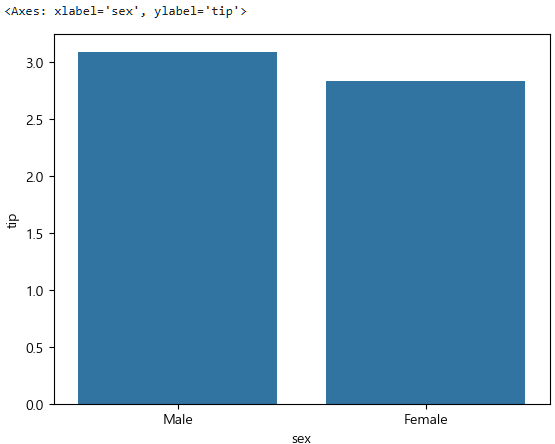
이렇게 sample 데이터에서 차이가 나는 것을 확인했는데,
이제 모집단에서는 어떤지 검정을 해보자.
먼저 정규성/비정규성을 확인하자.
귀무가설: (모집단일때) 남녀간 팁 평균의 차이가 없다.
대립가설: (모집단일때) 남녀간 팁 평균의 차이가 있다.
stats.normaltest(tips["tip"])NormaltestResult(statistic=79.37862574074785, pvalue=5.796294322907102e-18)pvalue < 0.05 -> 비정규이고 2집단이므로 ranksums() 함수를 사용한다.
tips_m=tips[tips["sex"]=="Male"] # tips.query(" sex == 'Male' ")
tips_f=tips[tips["sex"]=="Female"]
tips_m.shape, tips_f.shape((157, 7), (87, 7))2집단(남/여) -> Wilcoxon Test(윌콕슨 검정) -> stats.ranksums()
stats.ranksums(tips_m["tip"], tips_f["tip"])RanksumsResult(statistic=0.8710758231820401, pvalue=0.383712753987847)pvalue 0.38 > 0.05 유의수준 -> 귀무가설 참, 귀무가설 기각 실패, 남녀 팁 평균의 차이가 없다.
- 요일에 따른 팁 차이
지금까지 한 내용들을 보면 전체 과정이 이와 같다.
DDA로 전체 구조 파악 -> 그룹별 팁 평균, 그래프(EDA), 검정(CDA)
이제 찾아볼 성별, 흡연여부, 식사타임, 요일 각각에 따른 팁 차이를 볼때
방금 팁은 비정규임을 알아냈다.
그리고 집단의 개수를 찾아야하는데, 성별과 흡연여부, 식사타임은 2개인데,
요일인 경우에는 집단이 3개 이상이다. 따라서 이 경우는 어떻게 하는지 알아보자.
3개 이상인 경우에는 stats.kruskal()을 사용한다.
요일 그룹별 팁 평균을 파악하자.
tips.groupby("day", observed=False)["tip"].mean()day
Thur 2.771452
Fri 2.734737
Sat 2.993103
Sun 3.255132
Name: tip, dtype: float64그리고 이를 그래프로 그리면
sns.barplot(data=tips, x="day", y="tip", errorbar=None)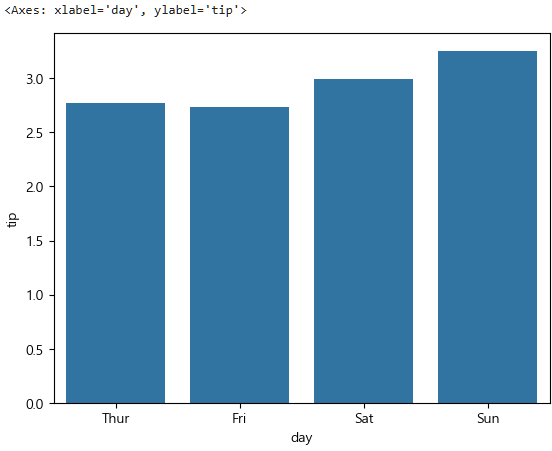
이제 원래라면 정규성을 파악해야하지만, tip이 비정규성임을 확인했기 때문에 생략하고
집단의 개수를 파악한다.
tips["day"].value_counts()day
Sat 87
Sun 76
Thur 62
Fri 19
Name: count, dtype: int64tips_day_sat=tips[tips["day"]=="Sat"]
tips_day_sun=tips[tips["day"]=="Sun"]
tips_day_thur=tips[tips["day"]=="Thur"]
tips_day_fri=tips[tips["day"]=="Fri"]
tips_day_sat.shape, tips_day_sun.shape, tips_day_thur.shape, tips_day_fri.shape((87, 7), (76, 7), (62, 7), (19, 7))이제 요일은 총 4개로 3개 이상인 kruskal()함수를 사용한다.
stats.kruskal(tips_day_sat["tip"], tips_day_sun["tip"], tips_day_thur["tip"], tips_day_fri["tip"])KruskalResult(statistic=8.565587588927054, pvalue=0.035660560194476144)결과로 pvalue 0.03 < 0.05 유의수준이므로 대립가설이 참이고, 귀무가설이 기각된다.
즉 요일별 팁 차이가 있다.
3.2.1.2. 정규성
정규성은 두 집단의 평균이 나오면 분산이 나오는데, 그 분산의 값이 같은지 다른지에 따라 등분산과 이분산으로 또 다르다.
그런데 문제가 이 Tips 데이터셋에는 정규성을 가지는 데이터가 없다.
정규분포가 나오려면 데이터가 많아야한다. 그러니까
⭐ 현재 데이터가 없으니, 정규성을 가진다고 가정하고 진행하자 ⭐
- 정규성 -> 등분산 / 이분산
- 등분산 검정 - Levene Test
- 귀무가설: 분산의 차이가 없다. -> 등분산
- 대립가설: 분산의 차이가 있다. -> 이분산
- 등분산 -> 2집단(T-Test / stats.ttest_ind( , equal_var=True)) / 3집단 이상(ANOVA Test / stats.f_oneway())
- 이분산 -> 2집단(T-Test / stats.ttest_ind( , equal_var=False)) / 3집단 이상(Kruskal Wilis Test / stats.kruskal())
tips_m=tips[tips["sex"]=="Male"]
tips_f=tips[tips["sex"]=="Female"]
tips_m.shape, tips_f.shape((157, 7), (87, 7))이제 등분산인지 이분산인지를 결정하기 위해 stats.levene()함수를 사용한다.
stats.levene(tips_m["tip"], tips_f["tip"])LeveneResult(statistic=1.9909710178779405, pvalue=0.1595236359896614)pvalue 0.15 > 0.05 유의수준 -> 귀무가설 참, 귀무가설 기각 실패, 남녀 그룹의 tip 분산의 차이가 없다.
즉 등분산이므로 x의 항목수를 봐야 한다.
집단이 남/녀로 2개이니까 Two Sample T-Test를 사용해야한다.
stats.ttest_ind(tips_m["tip"], tips_f["tip"], equal_var=True)Ttest_indResult(statistic=1.387859705421269, pvalue=0.16645623503456755)pvalue 0.16 > 0.05 유의수준 -> 귀무가설 참, 귀무가설 기각 실패, 두 집단의 차이가 없다.
그리고 여기서 equal_var는 등분산이니까 True이며, 이분산일때는 똑같이 사용하되, False로 바꿔줘야한다.
위에서 말했지만 이 데이터는 정규성을 가진다고 가정한 데이터였기 때문에 이분산에 대한 내용까지는 따로 다루지 않고 나중에 기회가 되면 다루겠다.
참고로 이분산이라면,
stats.ttest_ind(tips_m["tip"], tips_f["tip"], equal_var=True)
stats.kruskal(tips_day_sat["tip"], tips_day_sun["tip"], tips_day_thur["tip"], tips_day_fri["tip"])이와 같이 사용하면 된다.
3.2.2. x범주형(문자) y범주형(문자) - 두 집단간의 독립성 검정
3.2.2.1. Chi Square Test (카이 제곱 검정)
귀무가설: A항목과 B항목은 서로 독립적이다. (연관성이 없다)
대립가설: A항목과 B항목은 서로 의존적이다. (연관성이 있다)
앞서 귀무가설과 대립가설의 차이를 정리했었는데 여기서,
- 귀무가설: 보통 상태, 일반적인 상태, 평균의 차이가 없음, 상관성이 없음, 연관이 없이 독립적, 분산의 차이가 없음
- 대립가설: 의심하는 상태, 규명하는 바, 일반적이지 않은 이상상태, 평균의 차이가 있음, 상관성이 있음, 연관이 있으며, 분산의 차이가 있음
이 연관성에 대한 부분이다.
범주형인 성별과 흡연여부에 대한 두 집단의 독립성을 검정해보자.
- 귀무가설: 성별에 따라 흡연의 차이가 없다. (서로 독립)
- 대립가설: 성별에 따라 흡연의 차이가 있다. (서로 연관)
이에 대한 그룹화, 시각화, 검정진행한다.
이제 각 데이터를 살펴보면
tips["sex"].value_counts()sex
Male 157
Female 87
Name: count, dtype: int64tips["smoker"].value_counts()smoker
No 151
Yes 93
Name: count, dtype: int64이제 이 둘을 groupby로 묶어준다.
tips.groupby(["sex","smoker"], observed=False)["smoker"].size()sex smoker
Male Yes 60
No 97
Female Yes 33
No 54
Name: smoker, dtype: int64이를 표로보러면 문자-문자 이기 때문에 countplot을 사용한다.
sns.countplot(data=tips, x="sex", hue="smoker")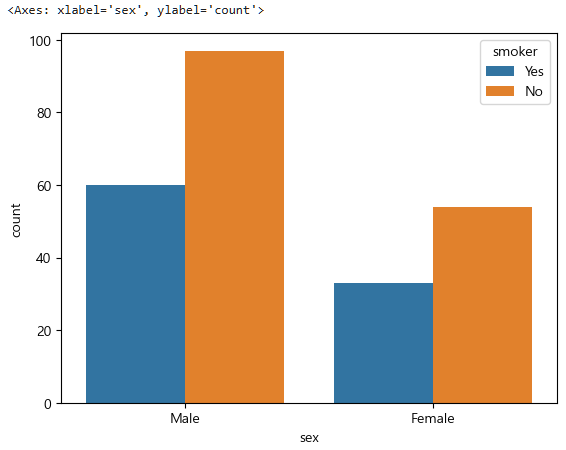
이제 그룹바이로 묶었는데 이를 Chi Square Test로 독립성을 검정하기 위해서는 먼저 분할표를 만들어서 분할표의 변수 독립성으로 접근해야한다.
파라미터를 교차표로 받기 때문에 먼저 pandas의 crosstab이라는 명령어로 교차표를 만든다.
(pivot_table과 비슷한 모양이다.)
df_crosstab=pd.crosstab(tips["sex"], tips["smoker"])
df_crosstab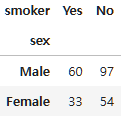
분할표의 변수 독립성에 대한 Chi Square Test은 chi2_contingency()함수를 사용한다.
다시 귀무가설과 대립가설을 보자면 아래 내용이었다.
- 귀무가설: 성별에 따라 흡연의 차이가 없다. (서로 독립)
- 대립가설: 성별에 따라 흡연의 차이가 있다. (서로 연관)
stats.chi2_contingency(df_crosstab)Chi2ContingencyResult(statistic=0.0, pvalue=1.0, dof=1, expected_freq=array([[59.84016393, 97.15983607],
[33.15983607, 53.84016393]]))
pvalue 1.0 > 0.05 유의수준이므로, 귀무가설은 참이고, 기각 실패, 성별에 따른 흡연의 차이는 없다.
여기서 이 dof(자유도)에 대해서는 나중에 다룰예정이다.
3.2.3. x연속형(숫자) y연속형(숫자) - 두 집단간의 상관 관계
정규형 : pearsonr()
비정규형 : spearmanr()
앞서 EDA에서 상관분석에 대한 내용에 대해 다뤘었는데, 그 내용과 동일하다.
따라서 corr()함수를 떠올릴 수 있는데, 사실 그 내용이 맞다.
사실 그냥 corr()함수를 쓰면된다.
원래는 지금까지 정규성일때와 비정규성일때를 나눠서 진행했었는데,
사실 corr()함수는 알아서 다 해준다.
그래서 굳이 나눠서 하려면 이 pearsonr() 함수와 spearmanr() 함수를 사용하면 된다.
어찌됐든 사용법만 조금 알아보자.
연속형인 데이터들을 뽑아보자.
tips_num=tips.select_dtypes(include=["number"])
tips_num.head()
식사 요금, 팁, 인원수 이들이다.
이제 corr()함수를 먼저 보면,
tips_num.corr()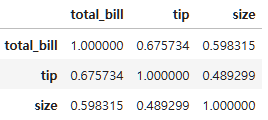
이렇게 식사 요금과 팁이 관계가 있다는 것을 알 수 있다.
그리고 이제 시각화를 해보면,
sns.scatterplot(data=tips, x="total_bill", y="tip")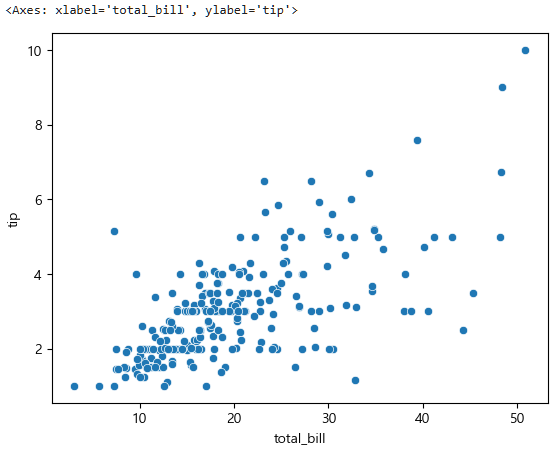
sns.scatterplot(data=tips, x="size", y="tip")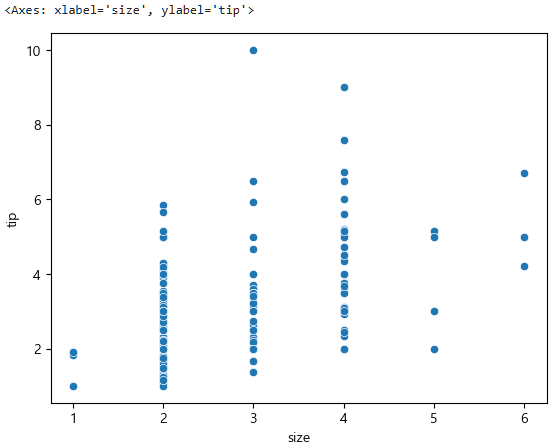
sns.scatterplot(data=tips, x="size", y="total_bill")
이렇게 나온다.
그렇다면 이제 corr는 다 나오는데, 특정한 것들만 보고싶다면,
pearsonr() 함수와 spearmanr() 함수를 사용하면 된다.
이제 그러면 식사 요금과 팁의 상관성을 보고싶다면,
- 귀무가설: 식사 요금과 팁의 상관성이 없다.
- 대립가설: 식사 요금과 팁의 상관성이 있다.
그런데 사실 둘 다 비정규성이었다.(둘 중 하나라도 비정규성이면 speramanr()사용)
stats.normaltest(tips_num["total_bill"])NormaltestResult(statistic=45.11781912347332, pvalue=1.5951078766352608e-10)stats.normaltest(tips_num["size"])NormaltestResult(statistic=64.55815532237287, pvalue=9.580202540024401e-15)그렇기 때문에 speramanr()을 사용한다.
stats.spearmanr(tips["total_bill"], tips["tip"])SignificanceResult(statistic=0.6789681219001009, pvalue=2.501158440923619e-34)pvalue 0.000...25 < 0.05 유의수준 -> 대립가설 참, 귀무가설 기각, 상관성이 있다.
그렇다면 만약 이들이 둘 다 정규성이었다면?
stats.pearsonr(tips["total_bill"], tips["tip"])PearsonRResult(statistic=0.6757341092113645, pvalue=6.692470646863819e-34)pvalue 0.000...669 < 0.05 유의수준 -> 대립가설 참, 귀무가설 기각, 상관성이 있다.
원래 비정규니까 값은 다르게 나온다.
📌 참고
x연속형(숫자) y범주형(문자)에 대해서는 머신러닝의 분류에측에서 다룰 예정이다.
💪 퀴즈
Q1. 추정과 검정의 차이점으로 옳은 것은?
1) 추정은 모집단의 파라미터를 추정하는 방법이며, 검정은 가설을 확인하는 과정이다.
2) 추정은 표본을 선택하는 과정이며, 검정은 데이터의 분포를 확인하는 과정이다.
3) 추정은 표본의 크기를 결정하는 것이며, 검정은 통계적인 모델을 만드는 과정이다. 4) 추정은 결과 값을 예측하는 과정이며, 검정은 실제 데이터를 분석하는 과정이다.
A1. 1
Q2. p-value가 0.03일 때, 유의 수준이 0.05일 경우 결론은?
1) 귀무 가설을 기각한다.
2) 대립 가설을 기각한다.
3) 귀무 가설을 채택한다.
4) 귀무 가설과 대립 가설을 모두 기각한다.
A2. 1
Q3. 점 추정과 구간 추정의 차이로 옳은 것은?
1) 점 추정은 모집단의 파라미터를 하나의 값으로 추정하고, 구간 추정은 모집단의 파라미터가 특정 구간에 있을 것이라고 추정한다.
2) 점 추정은 모집단을 추정하는 방법이고, 구간 추정은 표본을 추정하는 방법이다.
3) 점 추정은 구간을 사용하여 결과를 추정하고, 구간 추정은 하나의 값을 사용한다.
4) 점 추정과 구간 추정은 동일한 방법을 사용한다.
A3. 1
Q4. 구간 추정에 사용되는 개념으로 옳은 것은?
1) 신뢰도와 신뢰구간
2) 최소제곱법과 최대가능도 추정법
3) p-value와 유의수준
4) 분산과 표준편차
A4. 1
Q5. p-value가 다음과 같을 때, 의미하는 바로 옳은 것은?
- 귀무가설: 우리나라 20대의 평균 연봉은 2500만원이다.
- 대립가설: 우리나라 20대의 평균 연봉은 2500만원이 아니다.
- p-value: 1.6846793127448966e-251
1) 대립가설이 채택됐고, 우리나라 20대의 평균 연봉은 2500만원이다.
2) 귀무가설과 대립가설 모두 채택됐다.
3) 귀무가설과 대립가설 모두 기각됐다.
4) 귀무가설은 기각됐고, 우리나라 20대의 연봉은 2500만원이 아니다.
A5. 4
Q6. 정규성 검정에서 사용되는 함수로 옳은 것은?
1) stats.normaltest()
2) stats.ttest_ind()
3) stats.f_oneway()
4) stats.kruskal()
A6. 1
Q7. 등분산 검정에 해당하는 검정 방법으로 옳은 것은?
1) Levene Test
2) Wilcoxon Test
3) Kruskal Wallis Test
4) Chi Square Test
A7. 1
Q8. 비정규 분포를 가지는 3개의 집단의 검정 방법으로 옳은 것은?
1) T-Test
2) Kruskal Wallis Test
3) Levene Test
4) Wilcoxon Test
A8. 2
