Performance measure

1. Performance measure

내가 만든 모델이 얼마나 실제값을 잘 대변하는지 상대적인 비교를 하기 위한 지표

• MAE(Mean Absolute Error)
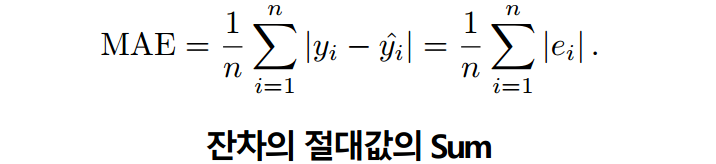  = np.abs(y-ŷ).sum()/len(y)로 구현 가능
  👉 0에 가까울수록 좋다.

*예측한 값과 실제값을 list형식으로 넣어줘서 수식을 수행하게된다.
from sklearn.metrics import median_absolute_error
y_true = [3, -0.5, 2,7]
y_pred = [2.5 , 0.0, 2, 8]
median_absolute_error(y_true, y_pred)

• RMSE(Root Mean Squared Error)
  가장 일반적으로 많이 사용
  

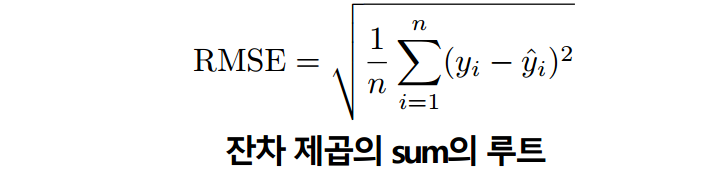
from sklear.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5 , 0.0, 2, 8]
mean_squared_error(y_true, y_pred)

• Regression metrics
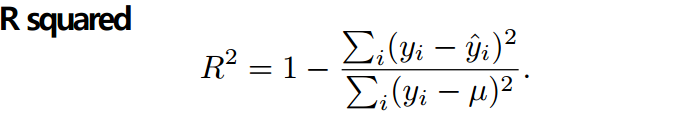  0과 1사이의 숫자로 크면 클 수록 높은 적합도를 가진다.

2. Training & Test data set

Training한 데이터를 다시 Test 할 경우, Training 데이터에 과도하게 fitting 된 모델을 사용될 수 있다.
모델은 새로운 데이터가 처리가능하도록 generalize 되어야한다.
👉 Training Set과 Test Set을 분리!
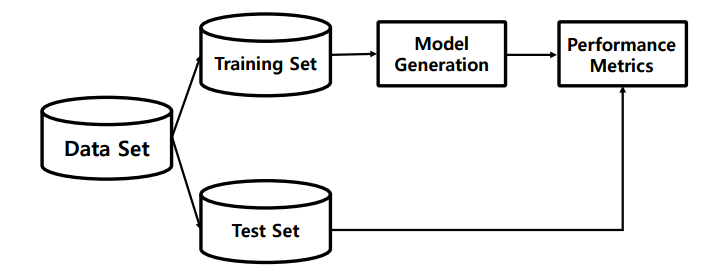Training set을 가지고 weight이 모두 다른 model을 만들어 RMSE를 통해 평가를 한다.
이때 Training set과 Test set을 나누는 것을 hold out Method(sampling)라고 한다.

• Sampling(Holdout Method)
  데이터를 Training or Test로 나눠서 모델을 생성하고 테스트하는 기법
  모델 생성을 위한 데이터 랜덤 샘플링 기법

import numpy as np
from sklearn.model_selection import train_test_split

X, y = np.arrange(10).reshape((5,2)), range(5)
X_train, X_test, y_train, y_test = train_test_split(
	X, y, test_size=0.33, random_state=42)

model_selection이라는 모듈에서 train_test_split을 나눈다.
x, y 데이터 parameter를 넣어주면 X_train, X_test, y_train, y_test로 나눠준다.

3. w/sklearn

scikit_learn을 이용하여 linear regression을 사용하여 실제로 y값을 예측.
1) 데이터 로딩

from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import numpy as np

boston = load_boston()
x_data = boston.data
y_data = boston.target.reshape(boston.target.size,1)
x_data[:3]

2) 데이터 스케일링
fit()을 통해 모델 생성 되었다 = weight값들이 정해졌다.
MinMaxScaler()를 활용하여 x_data를 scaling
⇒ 모든 데이터를 0~1 사이로 만들어주고 이것을 x_scaled_data로 부른다.

from sklearn import preprocessing
minmax_scale = preprocessing.MinMaxScaler().fit(x_data)
x_scaled_data = minmax_scale.transform(x_data)
x_saled_data[:3]

3) Train-Test Split
training set과 test set을 나눈다.
len(X_train) : len(X_test) = 8:2 비율로 데이터 샘플링을 해준다.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x_scaled_data, y_data, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

4) Linear regression fitting
fit_intercept : 상수항(절편값) 넣을 것인지 아닌지
copy_X : 데이터를 복사해서 사용하는 것이기 때문에 일반적으로 True사용
.fit() 피팅시킬때 train값만 따로 피팅

from sklearn iport linear_model
regr  linear_mode.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
regr.fit(X_train, y_train)

print('Coefficients:', regr.coef_)
print('intercept:', regr.intercept_)

5) 수식 결과 비교
reqr.predict(X_test) = ŷ = y의 예측

y_true = y_test 	#원래값
y_perd = reqr.predict(X_test_)	# 예측치

from sklearn.metrics import mean_squared_error
nq.sqrt(mean_squared_error(y_true, y_perd)
#RMSE로 성능을 비교해주기 위해 식 대입. 위의 문장과 의미가 같다.
# nq.sqrt(((y_True-y_perd) **2).sum() / len(y_true))

👉 normal equation으로 만든 sklearn에서 제공하는 linear regression모델로
이 linear regression모델을 만들기 위해 데이터를 train과 test로 나눈다.
먼저 train 데이터로 모델을 만든 다음 test로 성능을 평가한다.