Normal equation
Cost function을 최소화하는 방법
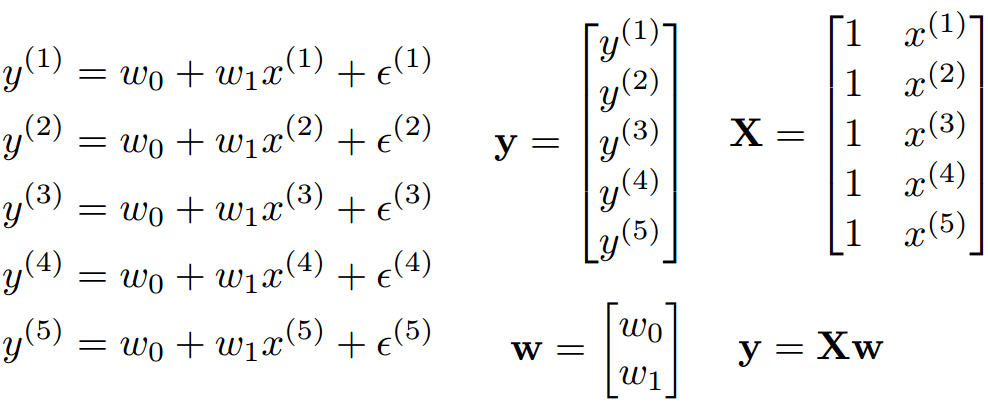vector는 소문자 bold, matrix는 대문자 bold, e는 잔차(에러)
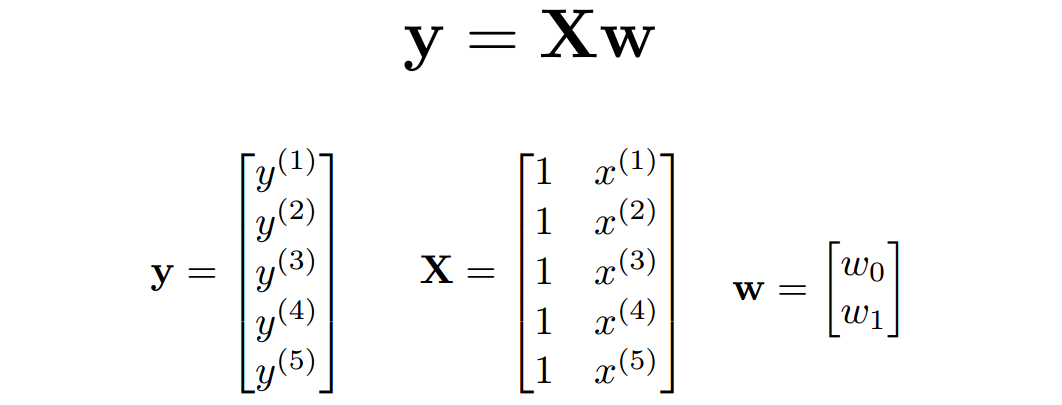
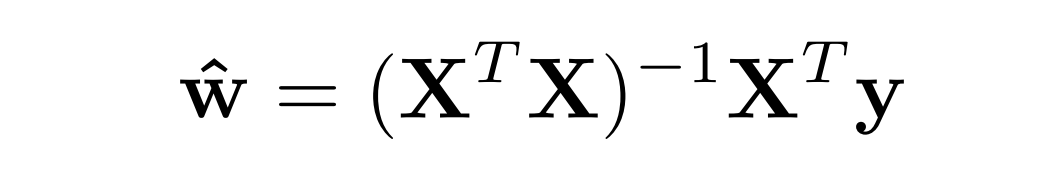
👉 X^T*X이 역행렬이 존재할 때 사용
Iteration등 사용자 지정 parameter가 없음
Feature가 많으면 계산 속도 느려진다.
Normal_equation_code
fit_intercept : 절편 값(w0)
→ fit_intercept=true : 절편값을 추가
→ fit_intercept=false : 절편값을 넣지 않는다/
coef : 계수값
fit() : matrix x에서 weight값(w)을 찾아내기 위한 함수
predict : 실험을 하고자 하는 x값(ŷ 예측값 반환)
import numpy as np
class LinearRegression(object):
def __init__(self, fit_intercept=True, copy_X=True):
self.fit_intercept = fit_intercept
self.copy_X = copy_X
self._coef = None
self._intercept = None
self._new_X = None
def fit(self, X, y):
"""
Linear regression 모델을 적합한다.
Matrix X와 Vector Y가 입력 값으로 들어오면 Normal equation을 활용하여,
weight값을 찾는다. 이 때, instance가 생성될 때, fit_intercept 설정에 따라
fit 실행이 달라진다. fit을 할 때는 입력되는 X의 값은 반드시
새로운 변수(self._new_X)에 저장된 후 실행되어야 한다."""
self._new_X = np.array(X) #넌파이array형태로 변환하기 위해
y = y.reshape(-1,1) #two dimensional로 바꿔줌
if self.fit_intercept: # 절편 추가
# data의 모든 개수, column 1개
intercept_vector = np.ones([len(self._new_X),1])
# 앞에 인데스는 모두 1(intercept_vector) 뒤에는 x0, x1, x2 ...할당
self._new_X = np.concatenate((intercept_vector, self._new_X),axis=1)
"""
fit_intercept가 True일 경우:
- Matrix X의 0번째 Column에 값이 1인 column vector를추가한다.
적합이 종료된 후 각 변수의 계수(coefficient 또는 weight값을 의미)는 self._coef와
self._intercept_coef에 저장된다. 이때 self._coef는 numpy array을 각 변수항의
weight값을 저장한 1차원 vector이며, self._intercept_coef는 상수항의 weight를
저장한 scalar(float) 이다.
"""
#역행렬
weights = np.linalg.inv(
self._new_X.T.dot(self._new_X)).dot #(X^T*X)^(-1)
(self._new_X.T.dot(y)).flatten()) #X^T*y
if self.fit_intercept:
self._intercept = weights[0] #w[0] = w0값이 들어간다.
self.coef = weights[1:] #구하려고 하는 계수값 = w1 ... w(n)
else:
self._coef = weights
"""
Parameters
----------
X : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
y : numpy array, 1차원 vector 형태로 [n_targets]의 구조를 가진다.
Returns
-------
self : 현재의 인스턴스가 리턴된다
"""
pass
def predict(self, X):
"""
적합된 Linear regression 모델을 사용하여 입력된 Matrix X의 예측값을 반환한다.
이 때, 입력된 Matrix X는 별도의 전처리가 없는 상태로 입력되는 걸로 가정한다.
fit_intercept가 True일 경우:
- Matrix X의 0번째 Column에 값이 1인 column vector를추가한다.
normalize가 True일 경우:
- Standard normalization으로 Matrix X의 column 0(상수)를 제외한 모든 값을
정규화을 실행함
- 정규화를 할때는 self._mu_X와 self._std_X 에 있는 값을 사용한다.
Parameters
----------
X : numpy array, 2차원 matrix 형태로 [n_samples,n_features] 구조를 가진다
Returns
-------
y : numpy array, 예측된 값을 1차원 vector 형태로 [n_predicted_targets]의
구조를 가진다.
"""
return None
@property
def coef(self):
return self._coef
@property
def intercept(self):
return self._intercept✔ jupyter notebook에서 실행할 때
import solution_linear_mode
import imp
imp.reload(solution_linear_mode)
lr = solution_linear_mode.LinearRegression(fit_intercept=True)
# 접합한걸 부른다음
lr.coef
lr.intercept # 실행시킨다.
Data Engineer