백준 #9095 : 1, 2, 3 더하기

이준영·2023년 4월 14일

DP 알고리즘

DP : 1,2,3 더하기(백준 #9095)

문제

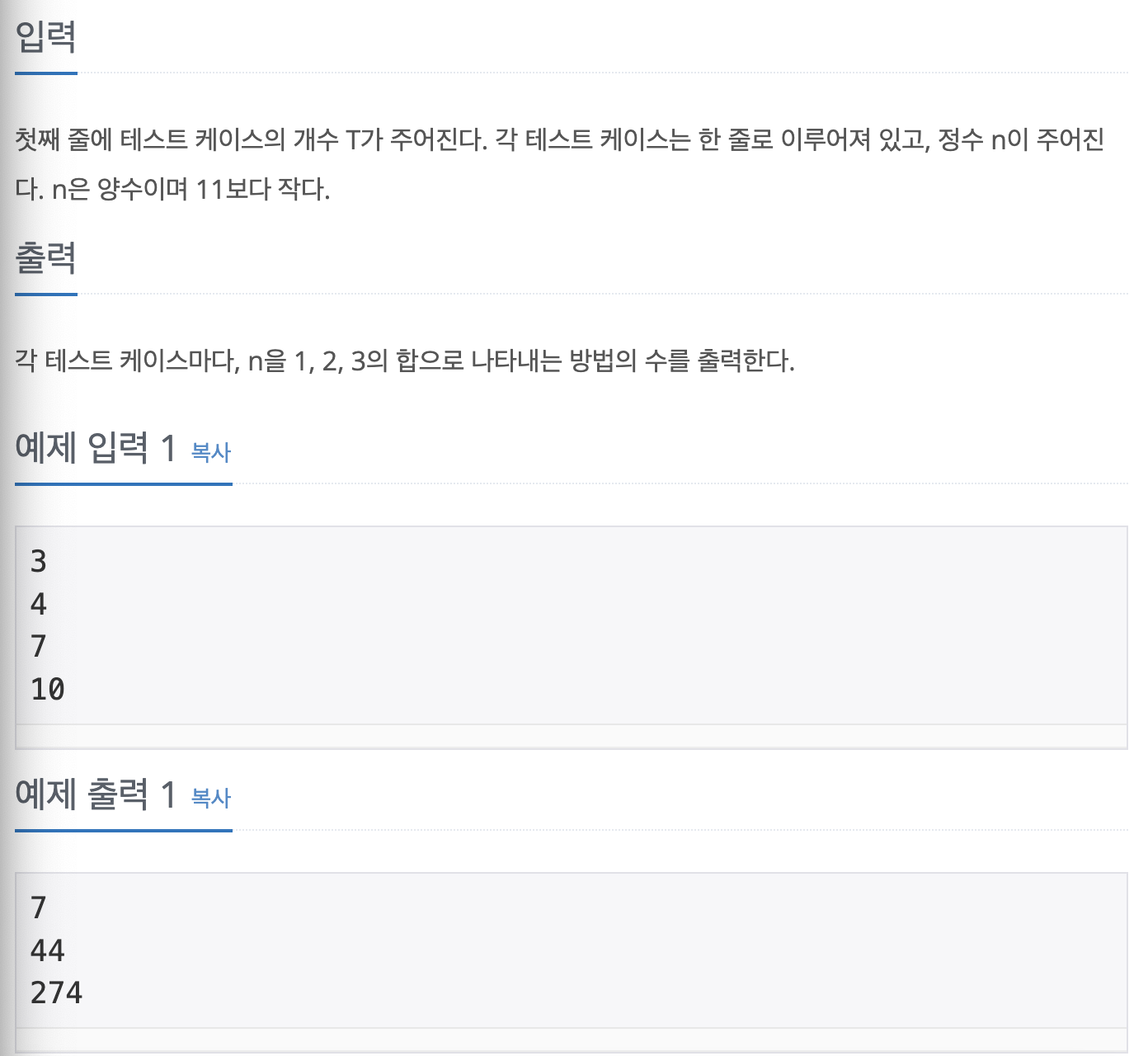
DP는 규칙 찾기가 중요한 듯 하다

규칙 찾기
1 = 1
2 = 1+1 / 2
3 = 1+1+1 / 1+2 / 2+1 / 3

4 = 1+3 / 2+2 / 3+1
5 = 1+4 / 2+3 / 3+2
6 = 1+5 / 2+4 / 3+3
...

결론 : f(n) = f(n-1) + f(n-2) + f(n-3)

이상하게 삽질하다가 규칙 찾아내는데만 한시간 넘게 걸렸다...

규칙을 알아냈으니 코드는 금방짜겠지?!

방법 1

def f(n) :
    if n == 1 :
        return 1
    elif n == 2 :
        return 2
    elif n==3 :
        return 4
    else :
        return f(n-1) + f(n-2) + f(n-3)

n = int(input("정수 n 입력"))    
print(f(n))

근데 이렇게 하면 n이 커질수록 연산시간이 심각하게 오래걸린다. 재귀함수의 한계...
이거 전에 배울때 무슨 용어가 있었던 것 같은데.. 기억이... 아무튼!!

해결방법 --👉 배열을 이용하자!!

방법2

n = int(input("정수 n 입력 : "))

dp = [1,2,4]

for i in range(3,n+1):
    dp.append(dp[i-1] + dp[i-2] + dp[i-3])

print(dp[n-1])

현재 dp[i] 기준으로 이미 지난 인덱스의 리스트 값(dp[i-1] ~ dp[0])은 저장돼있기 때문에 연산시간을 단축시킬 수 있다!

백준 문제 풀이

for문의 range를 (3,n+1)로 하면 append()를 이용했기 때문에 input을 반복해서 주면 문제가 생긴다.
append()는 배열의 마지막 index 뒤에 이어붙이는 것이기 때문에
두번째 input을 입력할 때부터 배열의 index가 내가 원하는 index 가 아니게 된다.

해결방법 :

배열을 초기화하던가 --> 너무 비효율적인듯 하다
배열 마지막 인덱스 다음부터 구하기 --> 이거다

dp = [1,2,4]

cnt =  int(input())

for i in range(cnt):
    n = int(input())

    for j in range(len(dp),n+1):
        dp.append(dp[j-1] + dp[j-2] + dp[j-3])
        
    print(dp[n-1])