[영상처리] 10. Image Compression

🔴 Image Compression

• 압축, 용량 줄이기
• 전달, 저장 시 사용
• Digital image를 표현하는데 필요한 data의 양은 줄이고, 가능한 한 많은 정보를 보존 하는 것이 목표

◾ data != information

• 아래 예시는 같은 정보를 가지지만 다른 data를 가진다.

◾ Image compression techniques

1. Lossless (무손실)

• 손실 없이 모든 정보를 다 가진다.
• 압축 영상을 복원한 영상과 원래 영상이 일치 -> 압축률이 낮다.
• Code

2. Lossy (손실)

• 몇몇 정보는 잃지만, 적당히 예측할 수 있다.
• 중복되거나 덜 중요한 정보 제거로 압축률이 높다.
• Image, Audio, Video

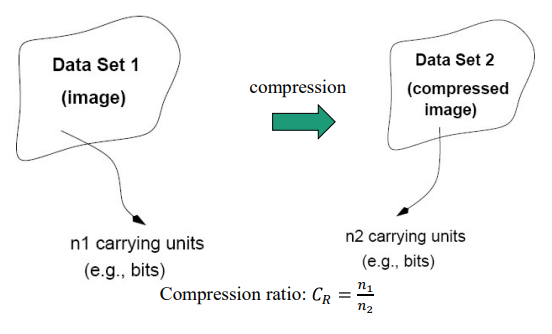
◾ Compression Ratio

• 원본데이터 비트 / 압축데이터 비트
• $C_R=1$: 그대로
• $C_R=2$: 0.5만큼 압축

◾ Relevant data redundancy

• 관련 데이터의 중복성(=압축해서 사라진 부분의 양)
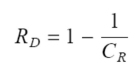
• ex) 90% 데이터 중복

◾ Compression by types of data redundancy

• 세가지 종류

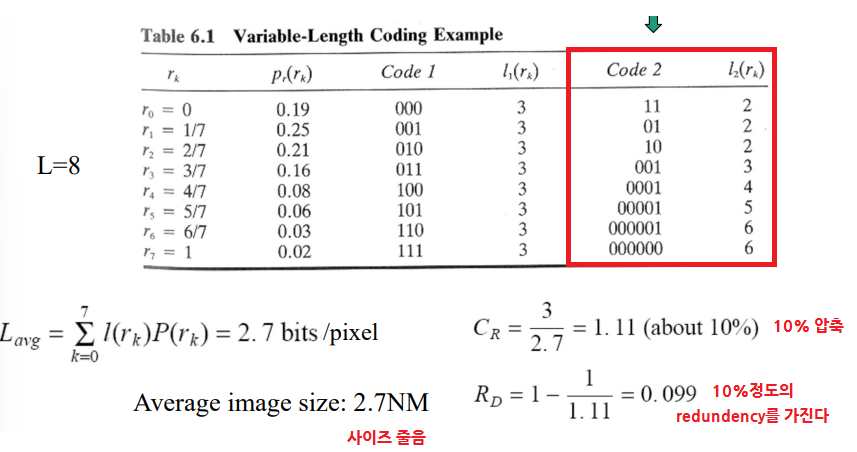
1. Coding redundancy

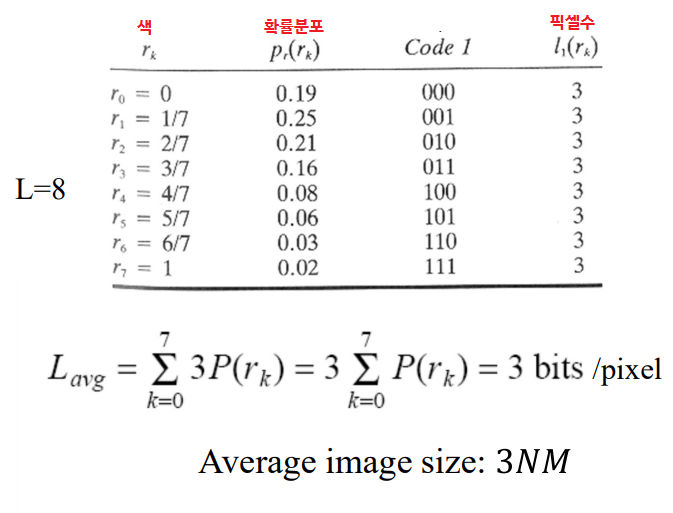
• 픽셀마다 다른 개수의 bit 쓰기 (밝기마다 비트수 조절!)
• k번째 gray level에는 $r_k$개의 bit만 쓰자 (검정은 1bit)
• 코드 워드당 평균 길이 / 픽셀당 평균 데이터(bit): 전체이미지에서 특정 픽셀이 나올 확률를 곱해서 구한다.
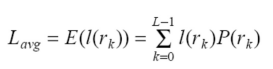
• 그래서 NXM의 이미지의 평균 사이즈는 아래와 같다.

◾예시

• 모든 픽셀이 3비트
• 픽셀마다 다르게

2. Interpixel(or spatial) redundancy

• 픽셀, 공간 중복성
• Pixel correlations을 따져서 픽셀 간 중복성 예측 (이웃으로 픽셀 상관관계를 따져 예측)
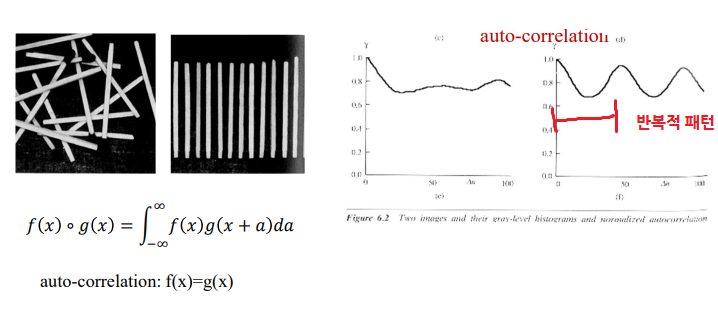
• 반복적 패턴을 가지면 하나만 하자
  
  
• +) 전달할 정보가 아래와 같다면, 굳이 회색 아니고 binary로 해도 정보 전달엔 문제 없음. 1024byte에서 1024bit로 1/8 감소

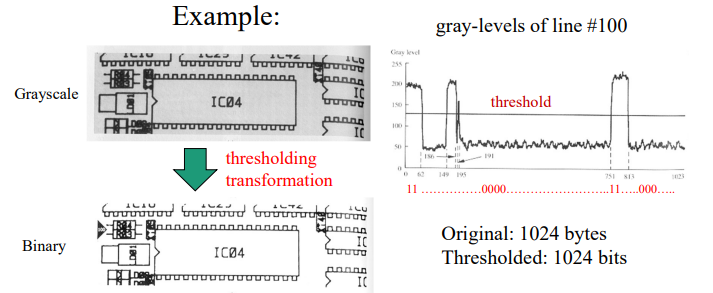
3. Psychovisual(or Irrelevant Information) redundancy

• 다른 data지만 사람눈에는 똑같아 보이는 경우

---

🟠 Information Theory basic

• 목표: 가능한 한 많은 정보를 보존하면서 데이터 양 줄이기
• 그래서 이미지의 정보를 보존할 수 있는 최소 데이터 양은 얼마일까? -> 엔트로피

◾ Entropy

• 변화가 있어야지 정보가 있는 것이다.
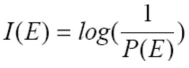
• 계속 똑같은 것(확률분포=1)은 정보 의미가 없다.
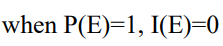
• 특별한 정보에 확률분포를 곱한 것이 엔트로피이고, 정보를 갖고 있는 것이 얼마나 자주 나오는가를 파악할 수 있다.

---

🟡 Compression Pipeline

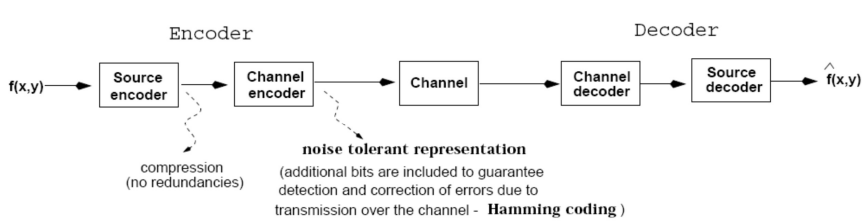
🟢 Symbolic Encoding

1. Huffman Coding (Adresses coding redundancy)

• 자주 나오는 건 짧게 하고, 자주 안쓰이는 건 길게 해도 괜찮다.

1. Encoding

• Symbol: 예를 들면 RGB에서는 0~255사이의 수
• Probability: 그 Symbol이 몇 번 나오는지

• (왼->오) 먼저, Symbol별로의 확률 분포를 정렬하고, 가장 낮은 두 확률을 묶어 아래와 같이 만든다.
• (오->왼) 뒤에서부터 code symbols을 정해준다.

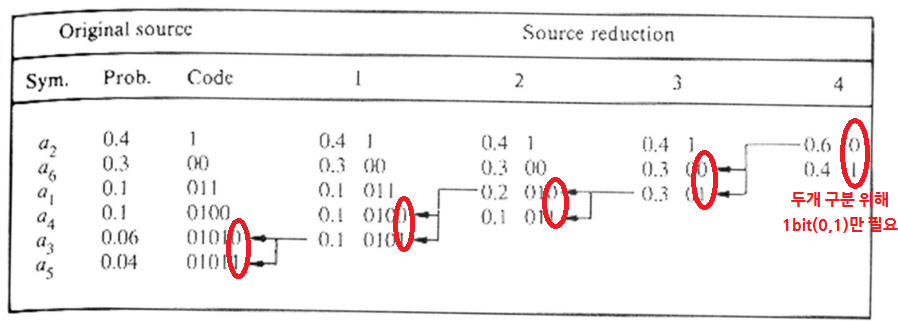
• 원래 각 symbol별로 3비트씩 했을 때와 비교하면 길이가 줄었다.

2. Decoding

• 위의 인코딩 표에서 오->왼으로 숫자 읽으면 됨

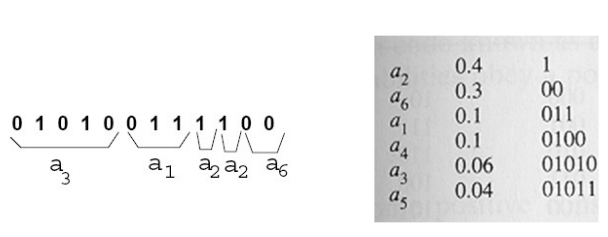
❗만약 비트 하나가 깨진다면, 그 이후의 모든 sequance가 망가짐

2. Arithmetic(Range) Coding (Adresses coding redundancy)

• 좀 더 효율적이고 Greedy하게 엔트로피 높이기 (Huffman은 한번에 하나씩 심볼을 정해주니까 비효율적일 수 있음)
• 주로 동영상 압축

3. LZW Coding (Adresses Interpixel redundancy)

• 가장 많이 사용
• Symbol Probabilities없이, 딕셔너리(테이블)을 가진다.
• 데이터가 올때마다 딕셔너리를 업데이트하면서 최적의 것을 찾아간다.
• 주로 GIF, TIFF, PDF 압축

1. Encoding

• 초기에는 0~255에 설정
• 들어오는 데이터를 써나감 (ex-39다음 39들어온다면 256번에 배치)
• 계속 딕셔너리에 써넣다가 딕셔너리에 이미 있는게 들어오면 그걸 쓰고,,
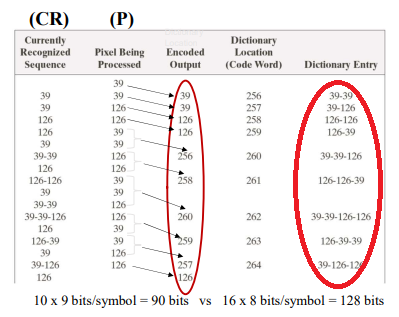
• 데이터들이 써나가다보면 자주 나오는 단어들도 등록될 것이고 그렇게 쓰면 됨
• 초기에 0~255 설정해놔서 딕셔너리에 없는 것은 없음

2. Decoding

• 디코딩하면서도 딕셔너리 만들 수 있음

❗만약 비트 하나가 깨진다면, 그 이후의 모든 딕셔너리가 망가짐

❗ Huffman과 Arithmetic 둘 다 하나만 망가져도 그 이후의 것을 해석할 수 없게되는 문제가 존재

4. Run-length Coding(RLC)(Adresses Interpixel redundancy)

• Run: 중복되는 Symbol
• Run이 있으면 수로 표시하기

5. Bit-plane Coding(Adresses Interpixel redundancy)

• 최상 비트 (8비트의 젤 앞자리)
• RLC쓰는데 좋음

---

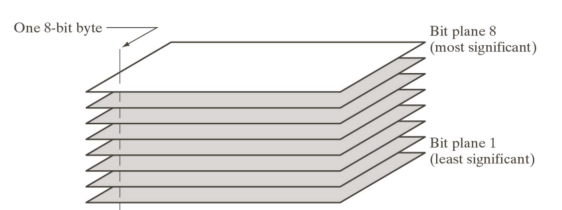
🔵 Mapping&Quantization

• 지금까지는 비슷한 애들이 많이 나온 경우
  = 엔트로피가 낮은 경우
  -> 엔트로피가 낮은 경우에~ Coding을 줄이는 방벙이었다.
• 그래서 엔트로피를 어떻게 낮추는지에 대해 알아본다.

1. Lossy Compression

• 엔트로피를 낮추는 것은 정보를 줄이는 것이다. (중복 데이터 많이 만들기)
• 정보의 손실이 있더라도 압축을 하는 경우
• 정보 손실을 어느정도 할 것인가?

1. 주관적 기준 - Subjective Fidelity Criteria
2. 객관적 기준 - Objective Fidelity Criteria

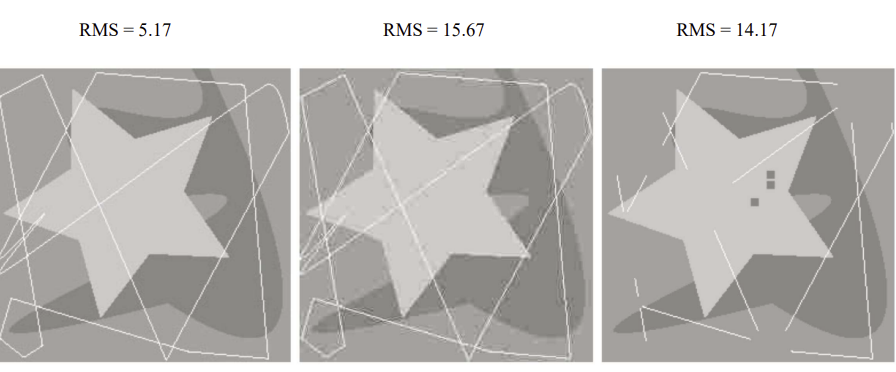
◾ RMS (Root mean square error)

• 차이의 평균을 구해서 얼마나 차이나는지를 파악한다.
• 크면 손실이 높다.

◾Mean square single to noise ratio(SNR)

• 원래 데이터 크기(분자)에 비해 에러(분모)가 얼마나 큰지도 비교한다.
• 예를 들어 전체적인 밝기 차이가 없는 곳에서는 1 차이도 티나는데, 반대는 아니니까

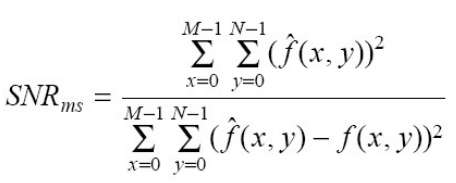
2. Lossless Compression

• RMS를 유지하면서 엔트로피를 줄여보자

◾ ex) Fourier transform

• DFT하고 보니 바깥 데이터가 별로 없다(high frequency). 없애도 되지 않을까?

• 근데 DFT는 좀 복잡해서 DCT를 쓴다.
• 주파수 영역에서 바깥 쪽의 고주파를 삭제하고 다시 공간 주파수로 전환한 경우, DCT가 가장 작았기 때문
  
  

◾ DCT

• cos을 두번 곱해서 주파수 영역으로 전환
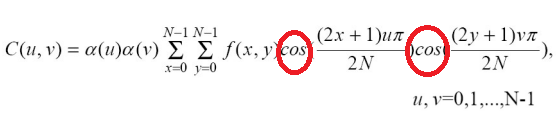
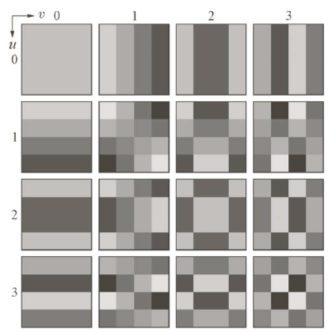
• 주파수 영역으로 전환할 때 한꺼번에 하는 것이 아니라, 이미지를 쪼갠 뒤에 각각을 Transform한다. 전환된 주파수 영역에서 바깥쪽을 잘라내서 공간 영역으로 다시 복구한 결과는 아래와 같다.
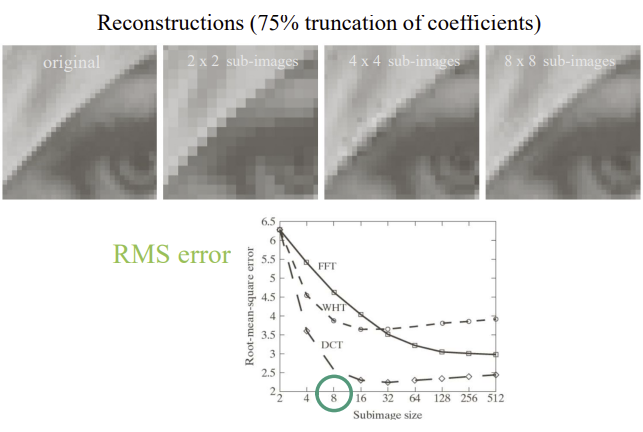
• 위 그림에서 8x8로 잘랐을 때가 에러가 가장 적으므로 8x8을로 자르도록 한다.

3. JPED Compression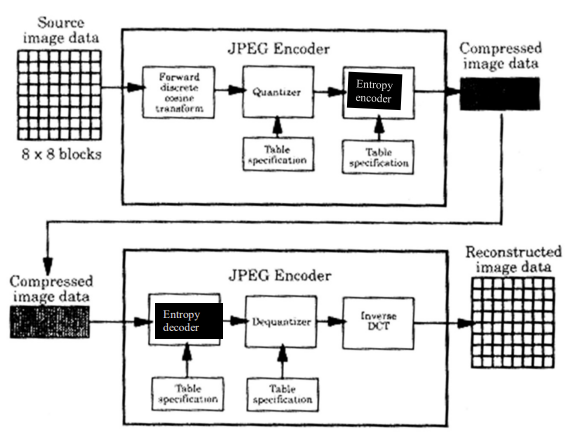

1. Divide

• 입력 영상을 8x8로 쪼갠다.

2. Shitf

• 각 이미지의 gray-level[0, 255]를 [-128, 127]로 바꾼다. (128 빼기)
• cos모양으로 맞춰서 DCT의 결과가 더 잘나오도록 함)

3. DCT

• 64개의 coefficients가 생긴다. (DC 1개, 나머지 AC 64개)

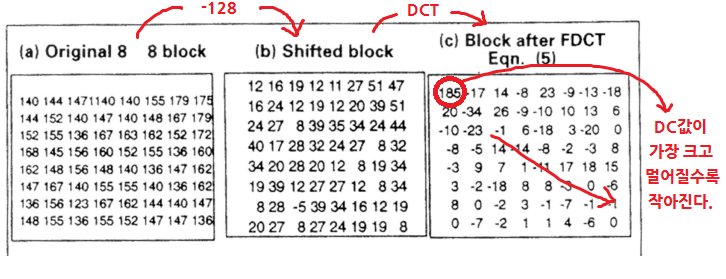
4. Quantize coefficients

• 주파수 영역에서의 삭제
• Q(Quantization array/table) 로 나누고 반올림 -> 비슷한 숫자들이 하나로 뭉쳐짐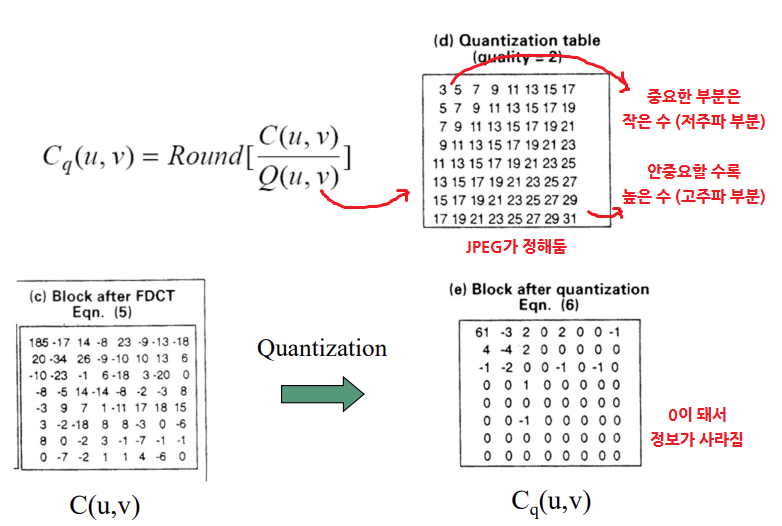
• 뒷부분이 거의 다 0이 될 수 있도록(최대한 뒤로 0이 몰려 있을 수 있도록) 지그재그 순서로 coefficientf를 나열한다.

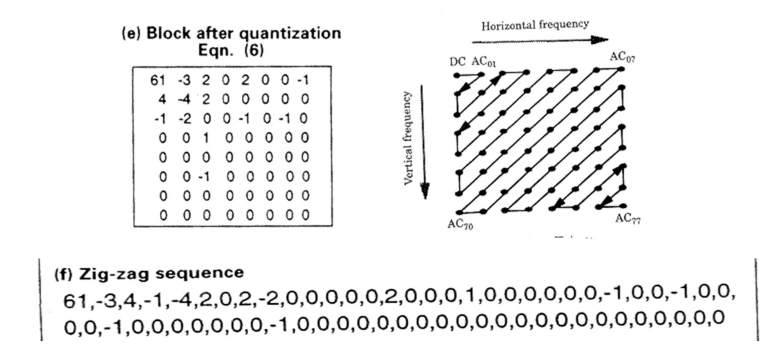
◾"Quality" parameter

• Quantization table를 결정하는 값
• quality가 높다 -> table값이 작다 -> 중요한 부분이라 작은 수로 나눈다. (저주파 부분)
• quality가 낮다 -> table값이 크다 -> 중요하지 않은 부분이라 큰 수로 나눈다. (고주파 부분)
• 하지만, 고주파 부분을 없애다보면 디테일이 사라지거나, 이미지에 하얀 블럭, 블럭형태의 경계, 저주파 영역의 노이즈 강조 등,, 문제가 발생할 수 있다.

5. Encode coefficients

• 엔트로피 인코더(ex-하프만)를 실행한다.

❗이것이 데이터를 작성한 것이고, 데이터 읽기는 이를 반대로 하면 된다.

4. Color JPEG

• RGB같은 것이 아닌 YCrCb라는 컬러공간을 사용한다.

◾YCrCb

• 밝기 + Chroma(Cr, Cb)
• 밝기를 구성하는 요소와, 색상과 채도를 결정하는 Chroma요소, 총 세가지 요소로 색을 구성한다.
• (0, 0)이 회색이다. (JPEG압축 과정에서 가장 많이 나오는 색이 회색이라서)
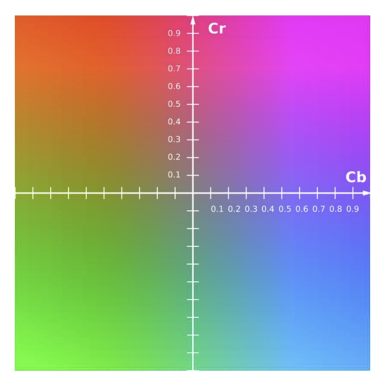
• 사람은 검흰인식보다 색상간 인식을 더 못하게 때문에 색(Chroma)의 크기를 이미지 크기의 절반으로 설정해서 엔트로피를 더 줄인다. (Cr 절반, Cb절반 하여 총 1/4 줄어듬)
• 크게 차이는 안나지만 확대하면 보인다

◾Progressive JPEG

• 과거에는위에서 아래로 스캔되어 인코딩했다면 (기본값)
• 요새에는 저주파에서 고주파 영역을 띄워주는 형식으로 인코딩한다.