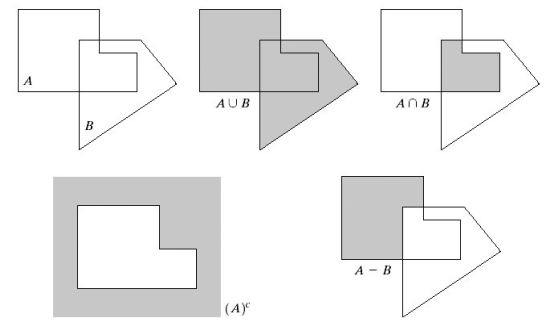
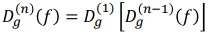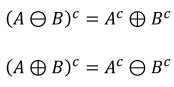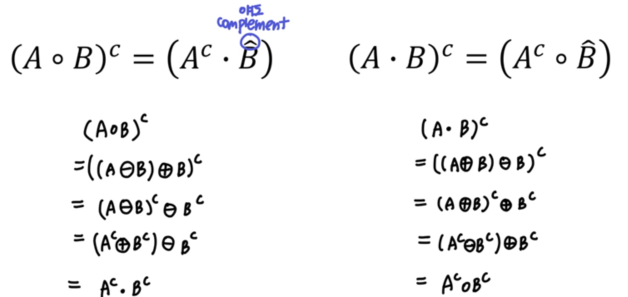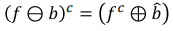◾ Mathmatic Morphology (수학적 모폴로지)
- 영역의 표현 및 설명에 유용한 이미지 구성요소를 추출할 때 사용
- 관심 객체의 검출을 쉽게할 수 있도록 영상 분할 결과를 단순화하는 방법

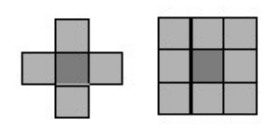
1. Structuring Element (SE)
- 구조적 요소란 원본 이미지에 적용되는 커널이라고 할 수 있다.
- 각 SE에 대해 원점, 모양, 크기 등을 정해야 한다.
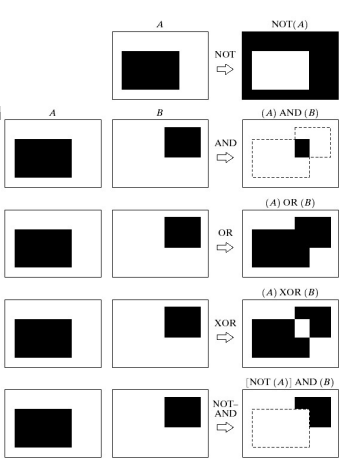
- 그래서 Morphological Operation이란, 모든 픽셀에 SE를 적용했을 때, neighbor들이 어떤 상황인지를 파악하는 것이다.
(Operation에 따라 Output pixel이 0 또는 1로 설정된다.)
2-1. Erosion (침식)
- 각 픽셀에 SE를 적용하여 하나라도 0이 있으면 대상 픽셀을 제거
- 오브젝트가 줄어든다. (Shrink)
- 작은 객체를 제거하는 효과
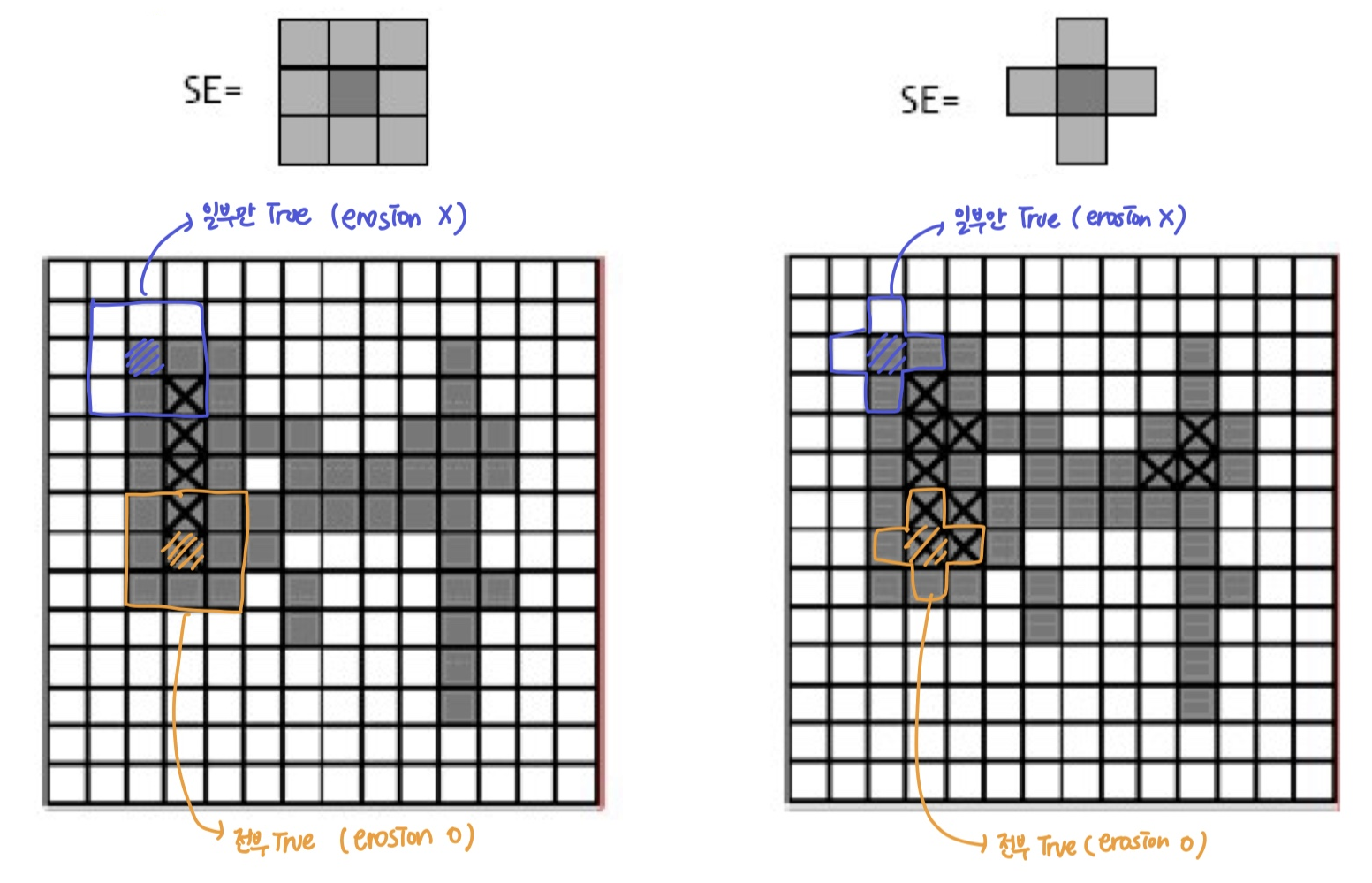
- SE
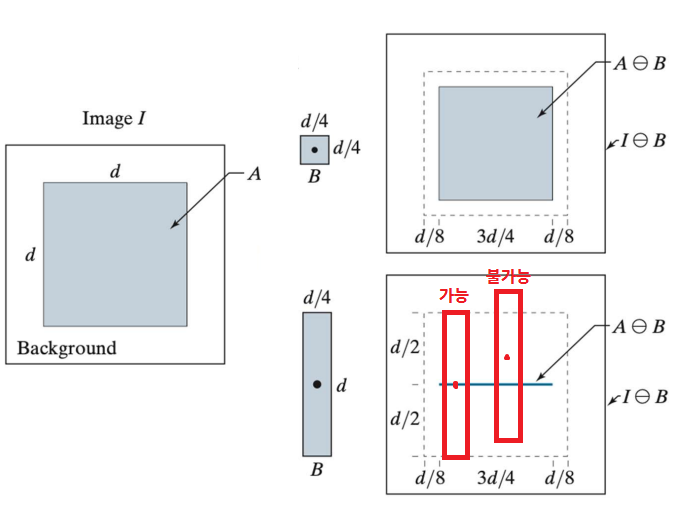
B로A를 Erosion: 한 픽셀z를 기준으로 SEB를 적용했을 때, 모든 이웃이 A에 포함되면 픽셀z적용 / 하나라도 포함되지 않으면 픽셀z제거
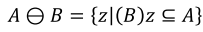
- SE를 작게 만들면 Shrink를 줄일 수 있다.
2-2. Dilation (팽창)
- 각 픽셀에 SE를 적용하여 하나라도 1이 있으면 대상 픽셀 사용
- 오브젝트가 확대된다. (Growing)
- 경계가 부드러워지고 작은 구멍을 채우는 효과
- SE
B로A를 Dilation: 한 픽셀z를 기준으로 SEB를 적용했을 때, 한 이웃이라도 A에 포함되면 SEB적용 (교집합이 공집합이 아니다.) / 한 픽셀z를 기준으로 하면 최소한 1개는 포함되므로 자기 자신은 무조건 포함이다.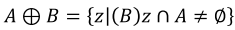
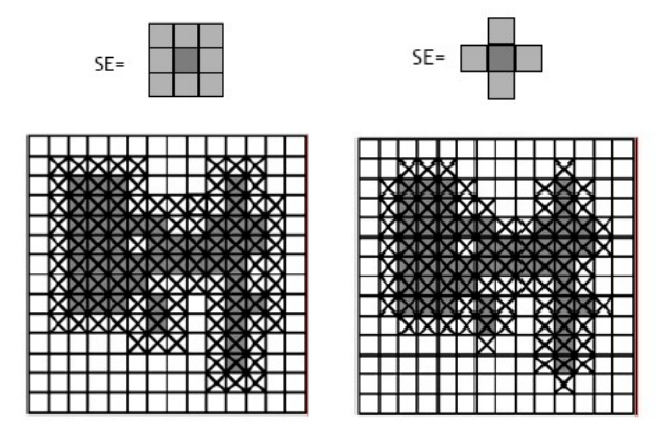
- ex) Binary형태인 글씨(글씨1, 종이0)를 OCR(문자 인식)할 때, 글씨의 선을 판단하는데 글씨가 끊어져있으면 인식하지 못한다. 그래서 Dilation으로 빈틈을 메꾼다.

◾ Duality
- Erosion과 Duality는 반대의 성질을 가진다.
✔️ 이제는 Erosion과 Duality를 결합한다.
- 작은 객체들은 삭제하고 구멍을 매꾸되, 나머지 부분에 영향을 미치지 않도록 한다. (연결은 하지만 뚱뚱해지지 않음~)
- Erosion과 Duality 중 어떤 것을 먼저 사용하는지에 따라 Opening인지 Closing인지 정해진다.
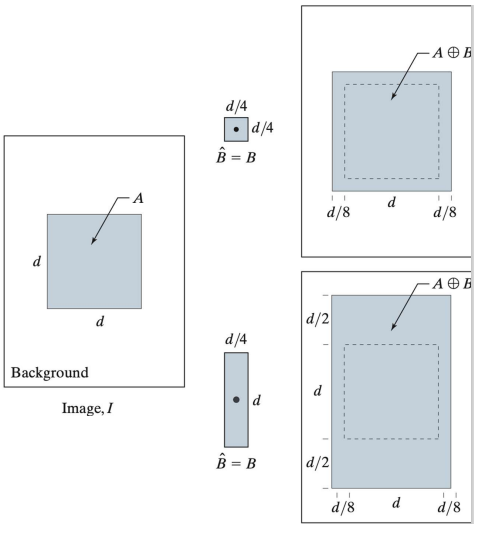
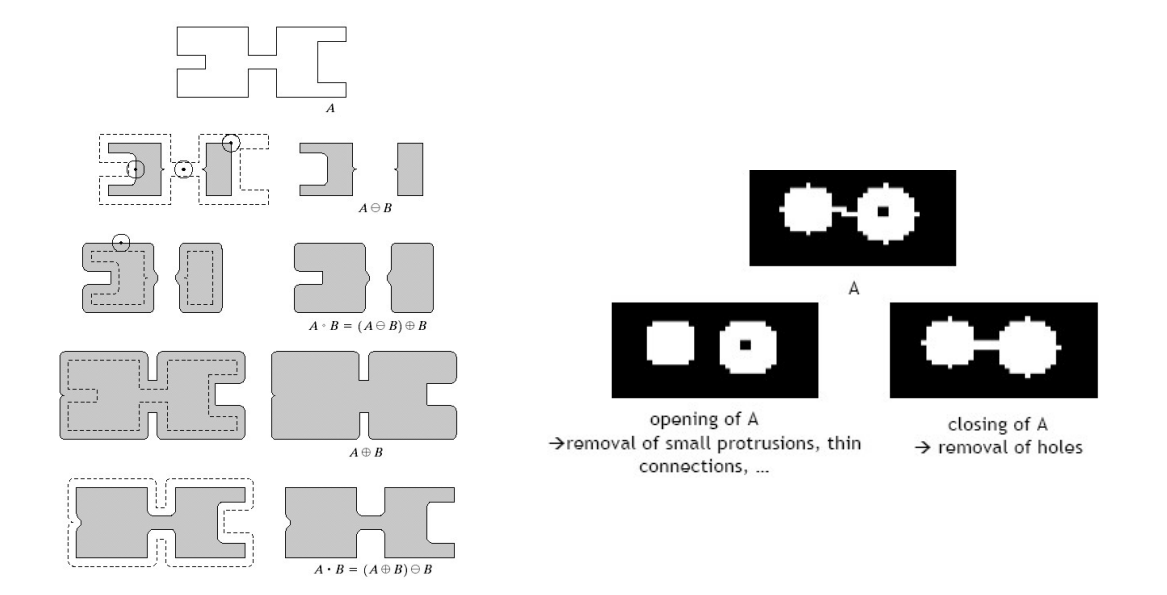
3-1. Opening (열림 연산)
- 선 Erosion, 후 Duality
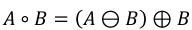
- 작은 객체 삭제 (Eleminates protrusions)
- 살짝만 연결된거 삭제 (Breaks necks)
- 경계 부드럽게 (Smooth contour)
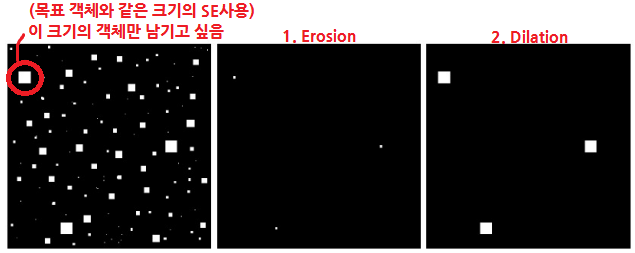
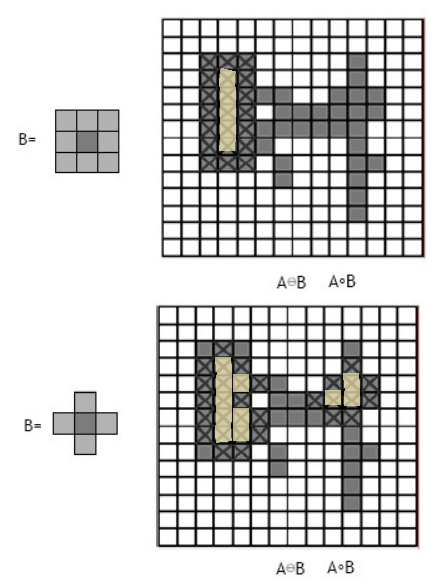
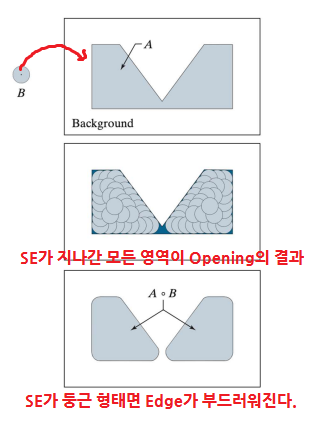
- 특징

- 특징
3-2. Closing (닫힘 연산)
- 선 Diality, 후 Erosion
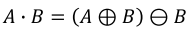
- 전체적인 윤곽 파악
- 경계 부드럽게 (Smooth contour)
- 좁은 틈 연결 (Fuses narrow breaks and long thin gulfs)
- 작은 구멍 제거 (Eliminates small holes)
- Fill gaps in the contour
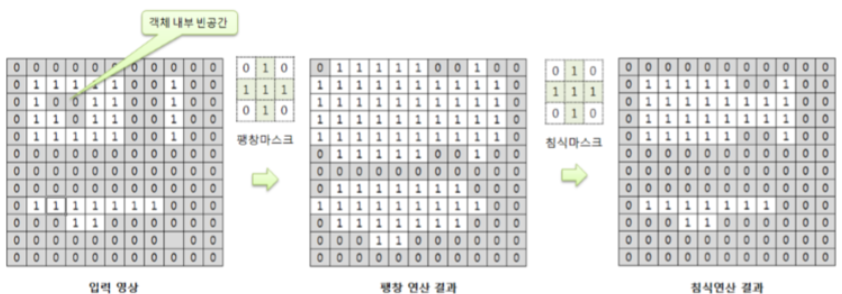
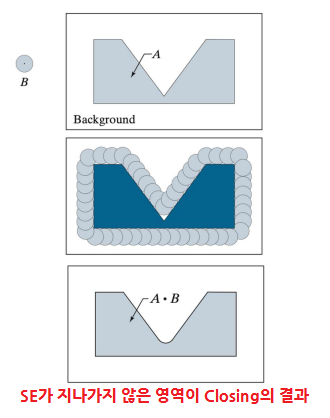
- 특징

- 특징
❗Opening과 Closing 반복하는 건 의미없다~~
◾ Duality
- Opening과 Closing은 반대의 성질을 가진다.
⭐⭐⭐증명
- 걍 풀다보면 나옴
3-3. Useful: Open/Close
- 각 특징에 맞게 적절하게 사용하면 된다.
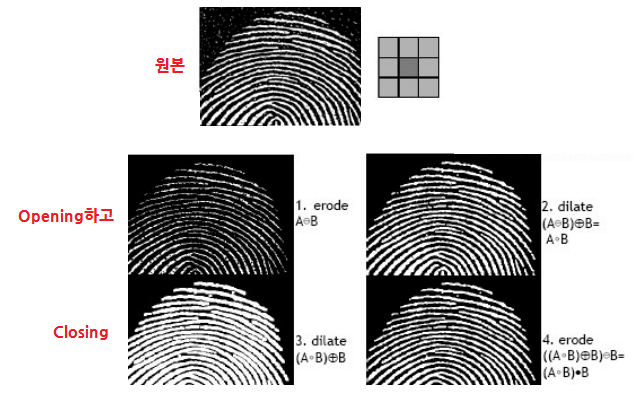
- +) Opening하고 Closing하면 끊어진 상태에서 구멍 매꾸기가 가능하다. (아래 기능)
◾Application: filtering
- 선의 구분이 중요한 경우 Opening하고 Closing하여 선이 이어지지는 않지만 구멍이 매꿔지도록 한다.
4-1. HMT (Hit-or-Miss Transformation)
- 영상 내에 존재하는 특정한 로컬 패턴 찾기
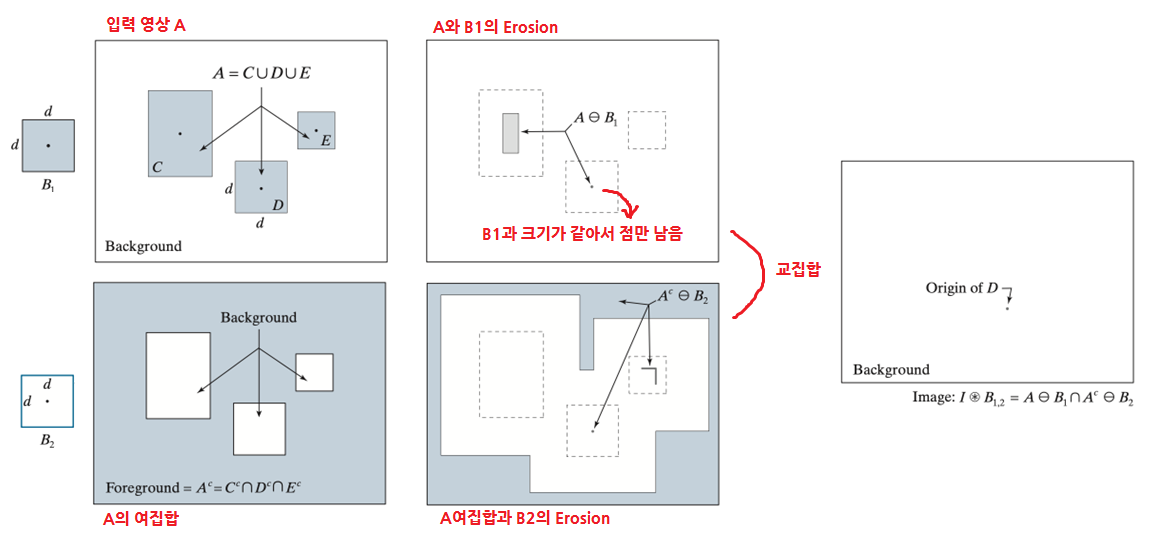
◾ HMT의 원리
- 2개의 SE가 존재한다. Object part는
B1, Background part는B2이다. A와B1의 Erosion과A의 여집합과B2의 Erosion의 교집합으로 구한다.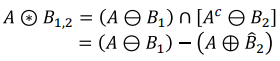
◾ HMT로 원하는 패턴 찾기
- 전형적인 HMT에서 찾고 싶은 패턴
B는 0과 1의 값을 가지는 픽셀들로 이루어져있다. - 특정 픽셀의
z주변에 있는 입력 영상I가 SEB랑 같다면 참이다.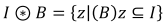
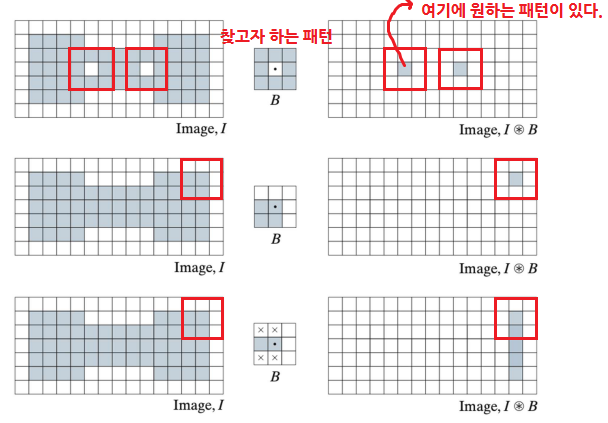
4-2. Boundary Extraction
- 경계 찾기
1. Outer boundary
- 자신은 F이고, 주변에 T 존재
- Dilation한 것에서 A를 뺀다. (강노에 없는 내용)
2.Inner boundary
- 자신은 T이고, 주변은 F
- A에서 Erosion한 것을 뺀다.
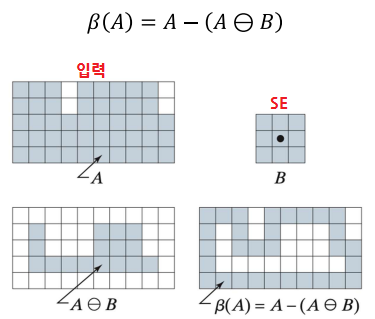

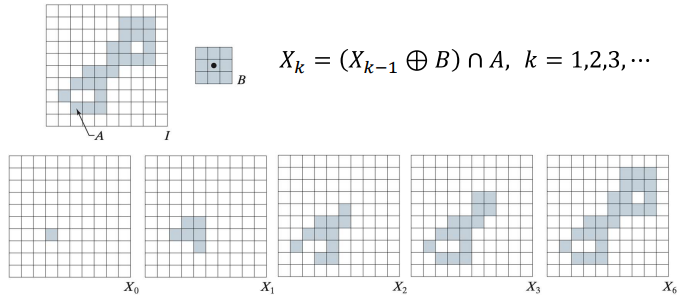
4-3. Region Filling
- 안쪽 색칠
- Dilation한 것과 A의 여집합의 교집합을 반복
- 오브젝트가 확대되지만 경계를 벗어나지 않는다.
- 시작점을 정하고, 변하지 않을 때까지 반복한다.
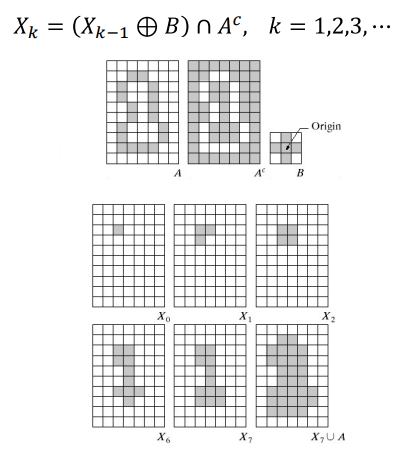

4-4. Extraction of Connected Components
- 연결되어있는 오브젝트 찾기
- 특정 픽셀이 다른 오브젝트와 연결된 길이 있는지 찾는 것이다.
- Dilation한 것과 A의 교집합을 반복
- 시작점을 정하고, 변하지 않을 때까지 반복한다.

✔️ 4-5, 6의 Thinning과 Thicking은 4-1의 HMT 사용
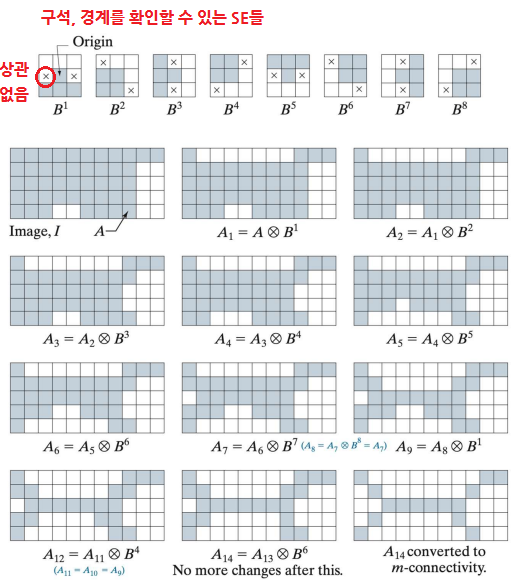
4-5. Thinning
- Boundary 중 Scelecton에 안들어갈 것 같은 픽셀을 삭제한다.
- 객체의 끝점이나 연결성 등은 유지하면서 객체의 모서리와 경계부분을 깎아 결과적으로 가는 객체를 만드는 것
- 구석, 경계점과 같은 특정한 패턴을 찾는 것이기 때문에 HMT를 사용
- HMT로 찾아낸 특정한 패턴을 가지는 픽셀을 입력이미지에서 빼는 것을 더이상 변화가 없을 때까지 반복
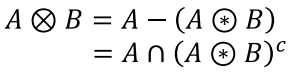
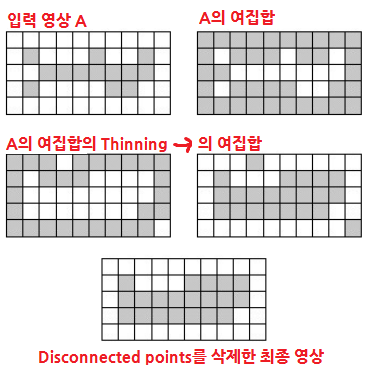
4-6. Thickening
- Thinning의 반대
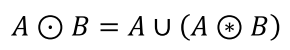
- 입력 영상의 여집합의 Thinning을 또 여집합하고 Disconnected points를 삭제해서 만들 수도 있다.
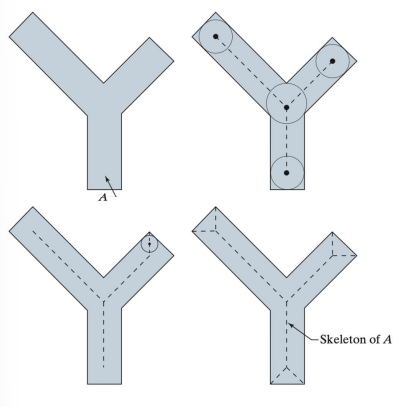
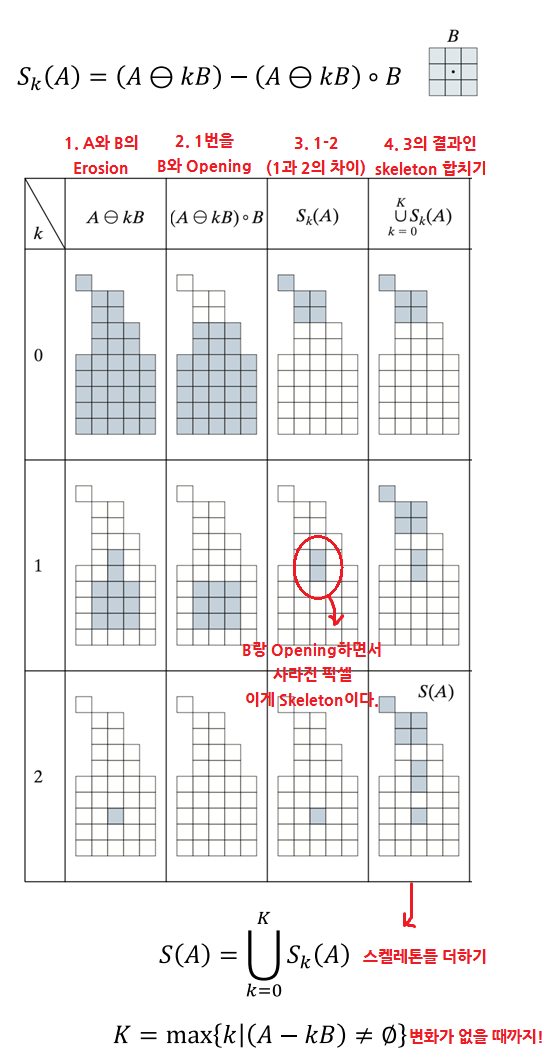
4-7. Skeletons
- 뼈대 찾기
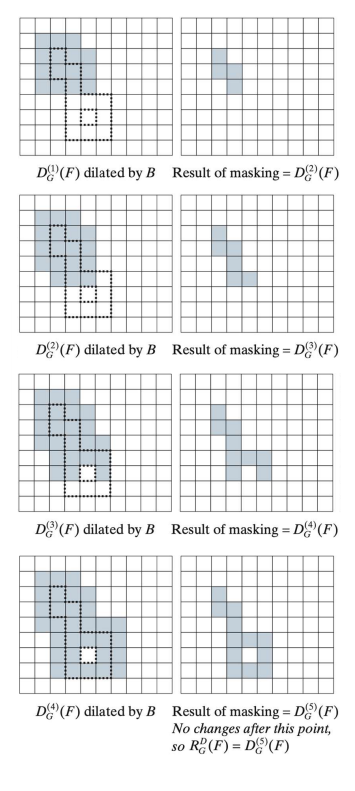
4-8. Morphological Reconstruction
- 특정 상황(ex-세로로 긴 객체)인 것들을 찾아내기
◾ Geodesic dilation
- Dilation으로 객체가 확장돼도, Mask 안에서만 확장됨 (범위가 제한된다.)
- Connected component와 같은 개념
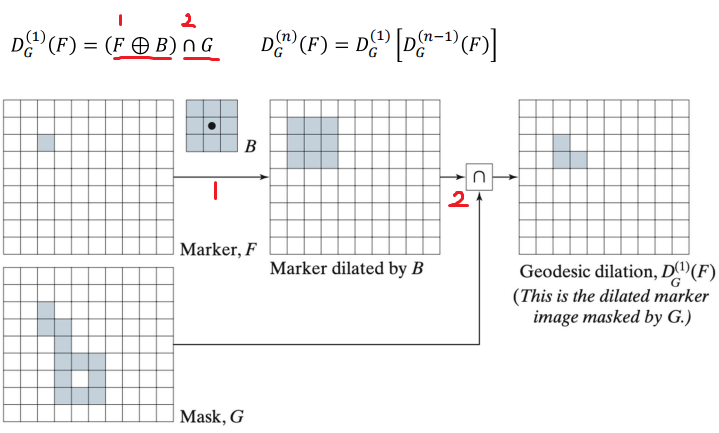
- Dilation하고 mask와 Union하기를 반복

5. Gray-Scale Morphology
- Gray-scale에서의 Morphology 연산은 좀 다르다.
- 검정 바탕
False에 흰 글씨True라고 생각해보자.
1. Erosion
- SE와의 연산 결과의 최솟값
- Erosion은 글씨가 가늘어지므로, 최솟값을 선택하여 주변의 어두운 색으로 따라가도록 함. (검정이 많아지면서 글씨 가늘어짐)

2. Dilation
- SE와의 연산 결과의 최댓값
- 위와 반대인 이유
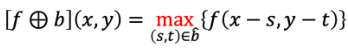
 (Treasholding 없이도 원한느 값을 찾을 수 있ㄷㅏ.) ?
(Treasholding 없이도 원한느 값을 찾을 수 있ㄷㅏ.) ?
☑️ Duality
- Gray Scale에서도 Erosion과 Dilation는 반대 성분을 가진다.
- 아래 식에서의 Complement는
1-값이다.
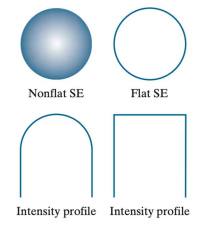
3. Nonflat SE
- 기존에 사용했던 0, 1로만 구분되는 SE말고, 연속적인 값을 가지는 SE를 사용한다.
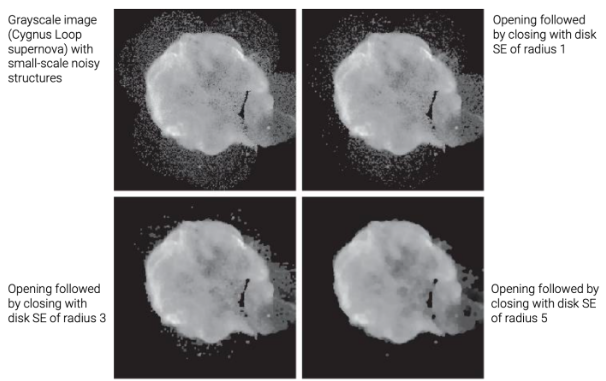
4. Morphological Smoothing
- 잡티만 없애는 Smoothing
- Erosion과 Dilation을 적절히 반복
5. Morphological Gradient
- 밝아지는 방향과 크기를 나타내는 Gradient 찾기
- Erosion과 Dilation의 차이를 계산하여 객체의 윤곽선을 찾는 방법이다.
- 커진거-작아진거 -> 차이를 알아내면 밝기가 급격하게 변하는 위치를 알 수 있다.
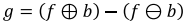
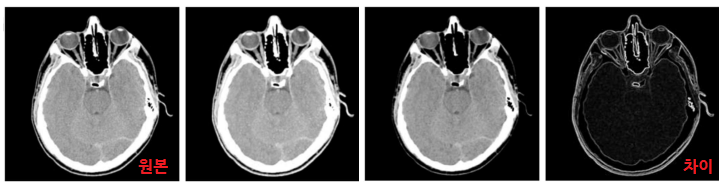
6. Top-Hat Transformation
- 이미지가 전체적으로 밝기가 다른 경우, Thresholding(이진화)으로 객체를 분리하기 어렵다.

- 그래서, 입력 영상에서 Opening을 빼는 Top-Hat transformation을 하고 Thresholding을 한다.
(SE는 하얀색 쌀알?이 포함되는 크기의 원 - 쌀알보다 커야됨 - 커야지 쌀알들이 사라지고 밝기가 다른 배경만 남음)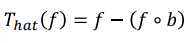

(어두운 배경에서 밝은 개체를 도드라지게 해준다.)
7. Textural Segmentation
- 영상의 객체 크기 분류
(배경이 1, 원이 0인 예시임)
8. Reconstruction
◾ Geodesic dilation
- Dilation하고 마스크
g와 교집합 - 이때, GrayScale에서 교집합은 Minimum이다.
- 그래서 위에 나왔던 것 처럼 객체는 확대되지만 마스크
g보다 커지지 않는다.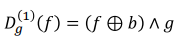
- Dilation하고
g와의 교집합을 반복한다.