
❗ 공식의 원리, 결과, 사용되는 것만 이해하기
https://hhlab.tistory.com/51
https://darkpgmr.tistory.com/171
🔴 Basics of Fourier Series & Transform
1. 기본 개념
◾ 주기 함수 (Periodic function)
- 모든 주기함수는 sin 또는 cos의 합으로 표현될 수 있으며, 각 sin 또는 cos은 서로 다른 주파수
frequencies와 진폭coefficient을 가진다. - f( x ) = f( x + c ) : 주기가
c인 주기함수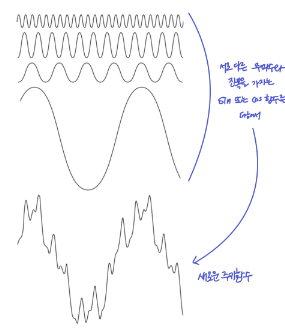
◾ 복소수 (Complex numbers)
- 실수와 허수로 이루어진 수
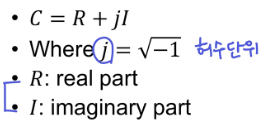
- 복소평면 위에서 복소수를 극좌표(Polar Coordinate)로 나타낸다.

◾ 오일러 공식 (Euler fomula)
- 복소수
cosθ+jsinθ를 간단히 표현하기 위한 공식 (정도로만 알고있자)
- ex) θ에 π를 대입하면 -1이 나온다.
2. Impulses and Their Sifting Property
(충격량과 선별 속성)
◾ Unit Impulse
- t가 0일 때에만 무한대 값을 가지고, 나머지는 0인 함수
δ(델타 함수) - 전체 범위를 적분했을 때, 1의 값을 가진다. (?왜지)
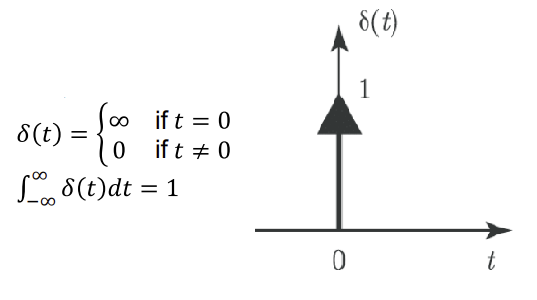
◾ Sifting Property
- 특정 함수
f에 위의 델타 함수δ를 곱하면 t=0이 아닌 부분은 전부 0이 되고, t=0인 부분의 값f(0)만 남게 된다. - t=0인 부분만 impulse하는 것이다.
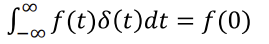
- 이 특징을 활용하기 위해 평행이동을 활용해여 impulse할 위치를 정할 수 있다. (아래 식은 t0만큼 평행이동)
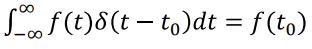
💭 impulse를 통해 내가 원하는 위치의 함수값을 얻어내는 방법이다.
◾ discrete한 값에도 똑같이 성립되는 Impulses
- 교수님 말씀으로는 x가 0일때 무한대가 아니라 1이 더 맞을거라고는 하심
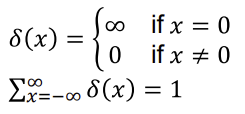
- sifting도 똑같이 성립한다.
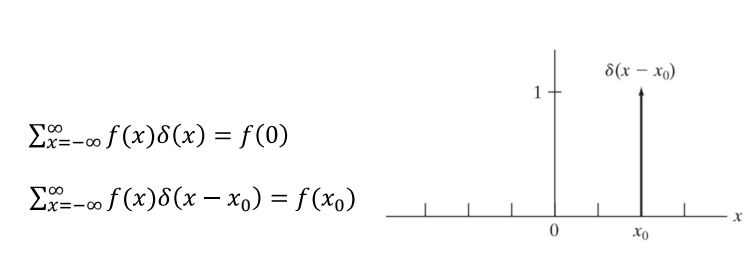
◾ Impulse Train
- 주기 ΔT로 델타 함수
δ가 반복 (주기 ΔT를 가지는 Impulse들의 합)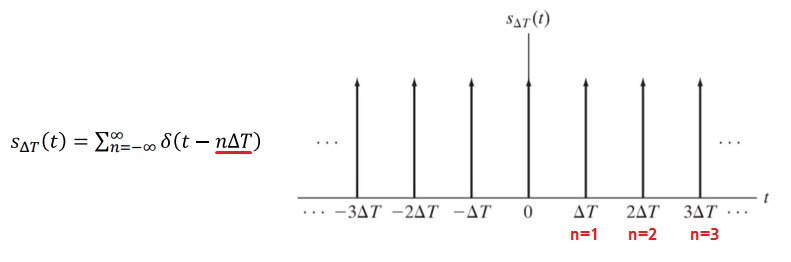
3. Fourier Transform (푸리에 변환)
◾ Image Transforms
- 공간 영역
x, y(spatial domain)의 이미지를 다른 영역u, v(another domain)으로 변환- 다른 영역에서 특정한 Operation 실행
- 다시 공간영역으로 돌리기 위해 Inverse Transform 진행
- 이때, 주파수 영역 (Frequency domain)으로 변환하는 과정을 푸리에 변환(Fourier Transform)이라고 한다.
- 푸리에 변환은 임의의 입력신호를 다양한 주파수를 갖는 주기함수(sin, cos)들의 합으로 분해하여 표현하는 것이다
- 하나의 신호는 여러개의 sin과 cos 신호의 합으로 표현될 수 있고, 이 신호들의 주파수 성분이 어떻게 구성되어 있는지를 파악하는 것이다.
- 아래 이미지에서 붉은 신호가 입력 신호, 뒤의 파란색 신호들이 푸리에 변환을 통해 얻어진 (원본 신호를 구성하는) 주기함수 성분들이다.
- sin과 cos 둘 다 있기 때문에 complex(복소수)형태로 표현된다.
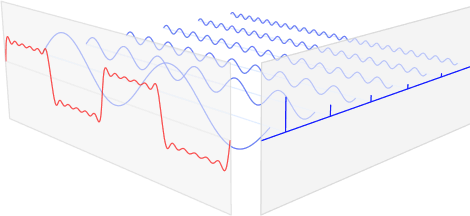
- 푸리에 변환을 사용하면 이미지 픽셀의 밝기 변화를 파형 또는 신호로 보고 주파수 분석을 적용할 수 있음
1. Transform
- Spatial domain
f(t)을 Frequency domainF(μ)으로 변환 - Transform함수
𝔉에는 위에 등장했던 오일러 공식이 포함됨 (파랑 형광펜) - 입력신호
f(t)가ej2πμt들의 합(적분)으로 표현된다는 의미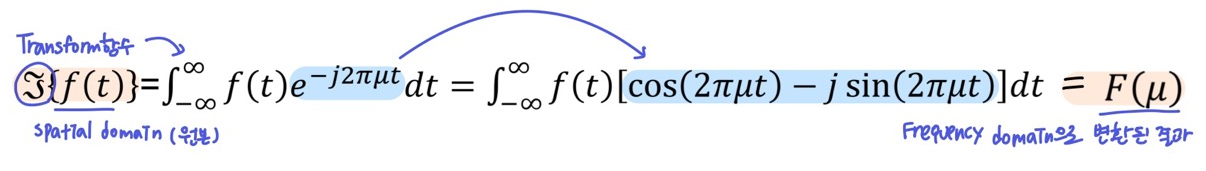
◾ μ와 cos2πμt의 관계
- 주기의 범위는 [0, 1/μ]이다.
- μ가 커질수록 한 cycle을 만드는 주기가 짧아진다. (cycle이 자주 생긴다.)
- μ는 cos2πμt의 주파수이다.
(t가 0~1인 범위에 몇개의 cycle이 들어가는가)- 주파수가 커지면 주기가 짧아진다.
f(t)는 다양한 주파수를 가지는 cos 함수들의 합F(μ)는 특정 주파수μ에 해당하는 cos함수의 진폭(정도)을 알려주는 함수f(t)를F(μ)로 변환하는 과정이 푸리에 변환이다. (진폭을 알면 변환할 수 있다.)
2. Operation
- 주파수 성분을 파악하고 분석
3. Inverse Transform
- 다시 Spatial domain으로 돌리기 위해 푸리에 역변환
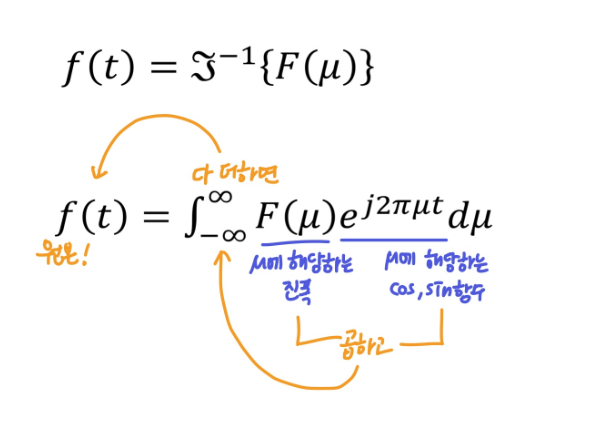
◾ 푸리에 변환 example
F(μ)는 복소수이고 복잡하기 때문에 보통 그래프에 나타낼 때는|F(μ)|를 사용한다.|F(μ)|는 Spectrum으로 푸리에 변환으로 얻은 각 주파수 성분의 강도(크기)이다.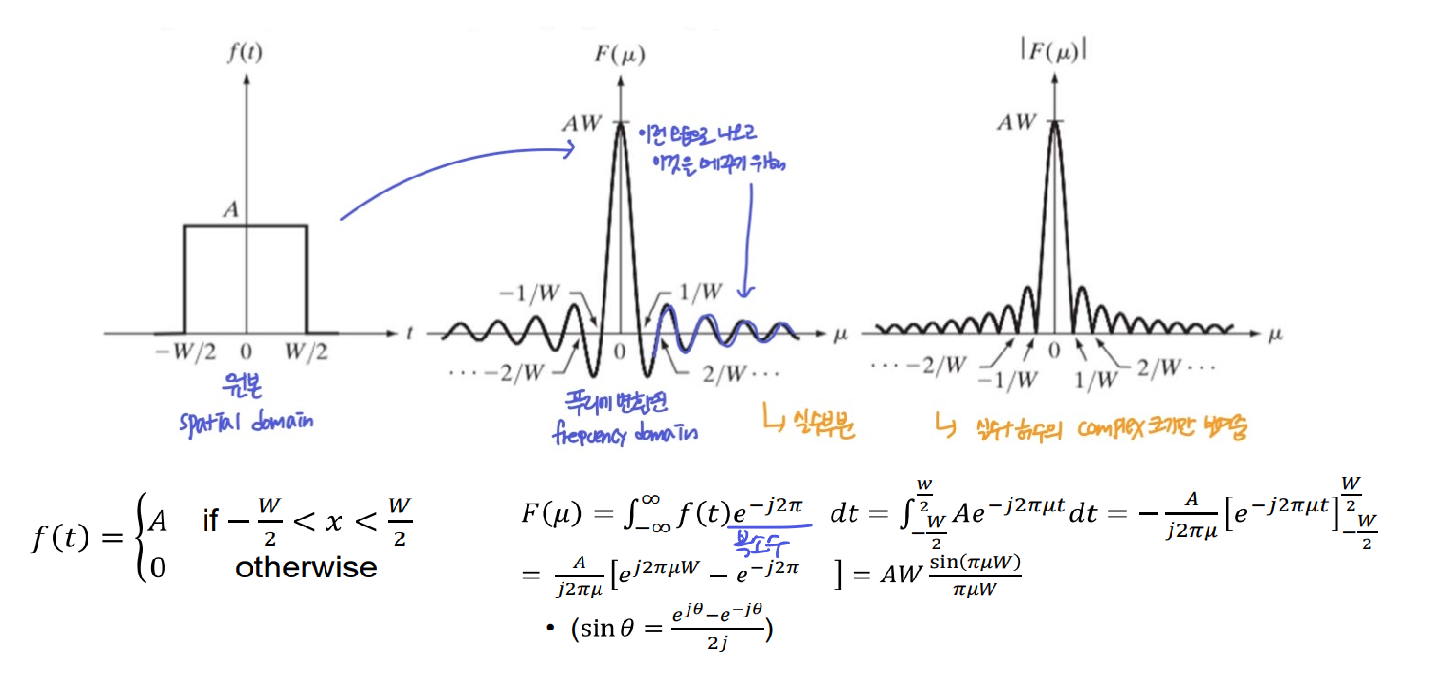
◾ Fourier Transform of a Unit Impulse
- Unit Impulse를 푸리에 변환하면 0일때만 의미있는 값이 나와 1이 나온다.
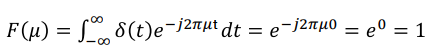
💭 0인 주파수에 해당하는 주기함수의 진폭이 1이다. 라는 의미? 근데 주파수가 0일 수 있나,,
- 원하는 값에 해당하는 결과 얻기 (sifting)
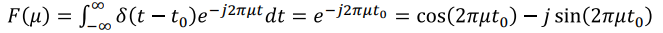
- Impulse train과 Transform
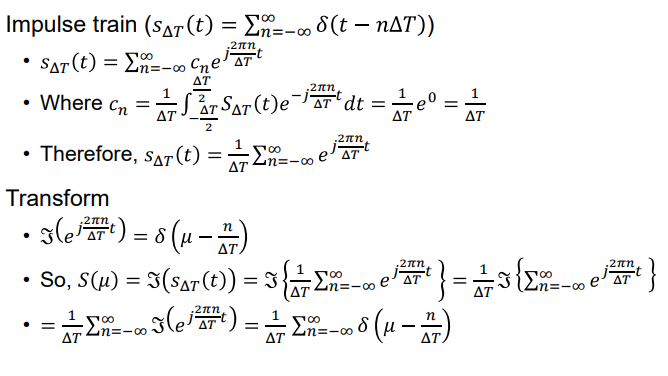
4. Convolution
- Spatial filtering과 비슷한 개념으로, 두 함수에 해당하는 값을 각각 곱하고 다 더하여 두 함수를 합치는 과정
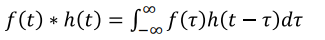
- Convolution한 값을 Transform하여 주파수 공간으로 변환하면, 아래와 같이
f와h를 각각 Transform한 값이 곱해진 결과가 나온다.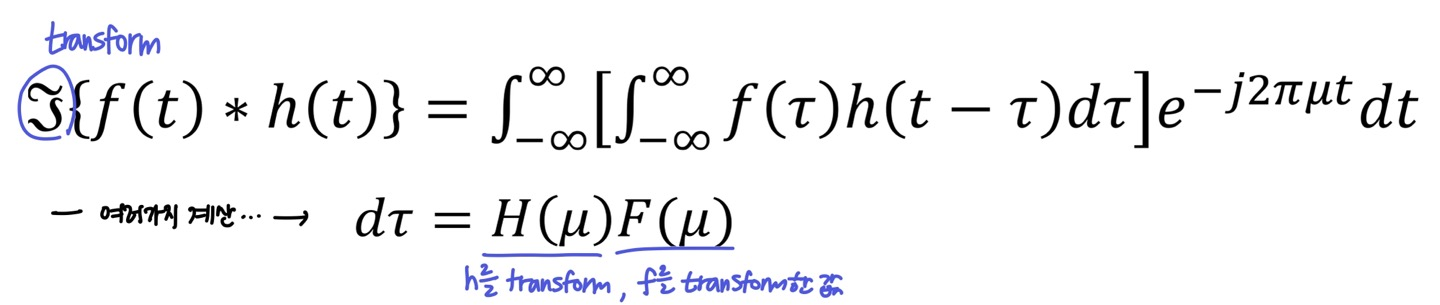
- 결론적으로 Spatial 공간에서의 Convolution 연산은 Frequency 공간에서의 곱셈 연산과 같다는 것이다.
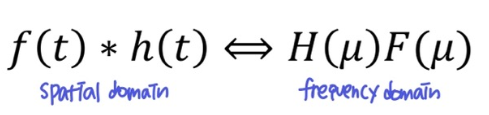
❗ 주파수 공간에서 더 간단히, 빠르게 연산할 수 있다는 것이다~ 결국 이게 목적이라 봐도 됨
🟠 Sampling & the Fourier Transform of Sampled Functions
1. Sampling
- 원본
f(t)에 Impulse train을 곱하면,ΔT주기에 해당하는f(t)값들만 남고, 이것을 점으로 표시하면 Sampling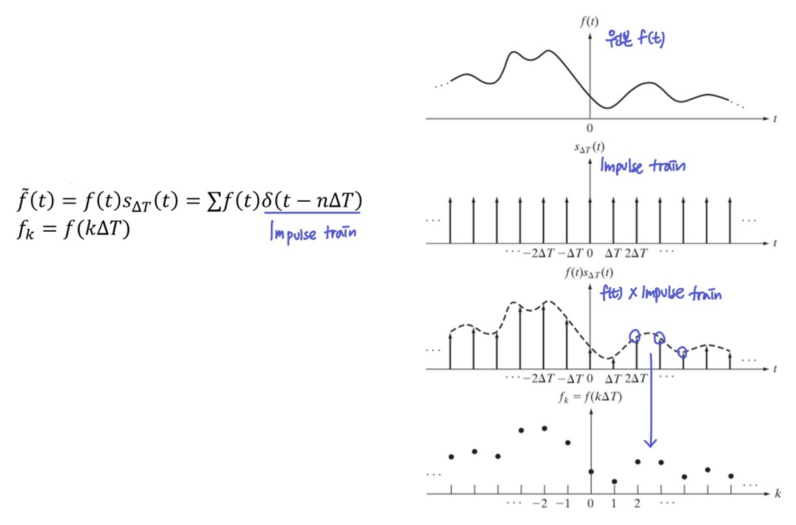
2. 잘못된 Sampling Frequency
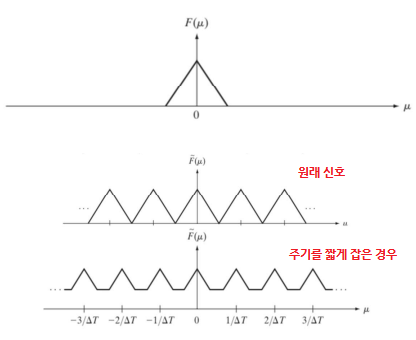
- Sampled Function을 Transform하고 얻은 표본화된(샘플링된) 이산 신호를 가지고 다시 원래 신호로 복구할 때,
- 주파수를 낮게 잡아(주기를 길게 잡아) Sampling했다면 Aliasing 문제가 생길 수 있다.
- 그래서 Sampling할 때, 원래 신호가 어떻게 생겼는지에 따라 다르게 해야한다.
3. Aliasing (Moire effect)
- 주파수가 높은(주기가 짧은) 신호를 듬성듬성 Sampling한 후, 원래 신호로 복귀하면 아래 예시 이미지처럼 원래 보이지 않던 패턴이 보이게 된다.
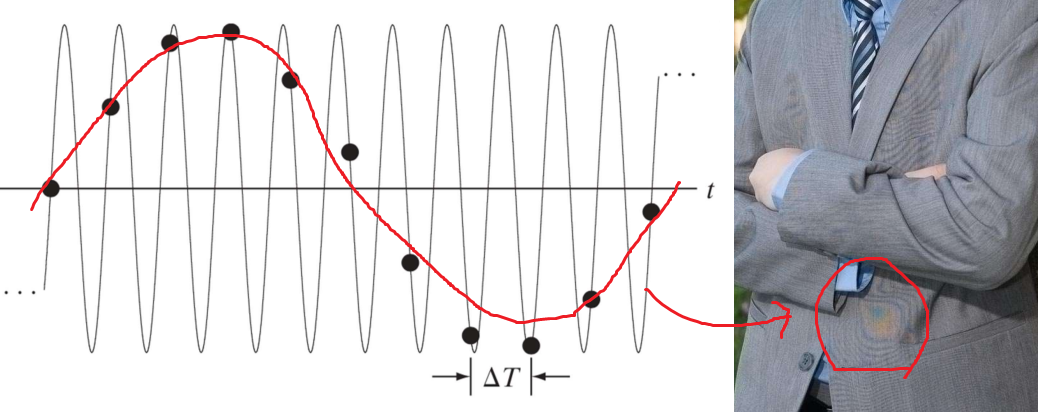
- 이러한 현상을 피하기 위해 2배 이상의 Sampling을 하는 Nyquist rate를 따라야한다.
4. Nyquist rate (올바른 Sampling Frequency)
- 원래 신호의 형태를 유지하기 위해서는 원래 신호가 갖고있는 주파수의 최댓값
μmax의 2배보다 큰 주파수1/ΔT(주기의 역수)로 Sampling 해야한다.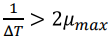
🟡 Discrete Fourier Transform
- Discrete하기 때문에 ∑의 형태로만 바뀔 것이고 더 간단해진다.(샘플링된 함수에 cos 또는 sin함수가 곱해진 것을 다 더한 것)
1. 이산 푸리에 변환 (DFT)
- 푸리에 변환은 보통 이산 푸리에 변환으로 나타난다.
- 컴퓨터로 실제 분석을 위해서는 샘플링된 이산 데이터를 사용하기 때문이다.
2. 고속 푸리에 변환 (FFT)
- Fast Fourier Transform
- 이산 데이터에 대한 Transform을 더 빠르게 처리하기 위한 방법이다.
❗ 지금까지의 내용은 t에 대한 1차원 transform이고(실제의 연속적인 데이터), 2차원 transform은 x, y에 대한 것이다(이산적인 이미지).
🟢 Extension to Two Variables
1. Two-Dimensional Sampling
- trasnform된 주파수 영역이 2차원인
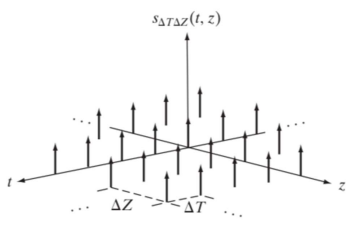
F(u, v)의 형태 - Impulse train도 2차원이고, Sampling조건도 각 차원만 나눠져있을 뿐 위와 동일하다.
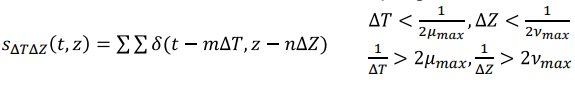
- 가로로 sin 또는 cos파, 세로로 sin 또는 cos파가 있고 두개가 합쳐져서 모양이 생긴다.
➕ 이미지에서의 Aliasing
2. 2D DFT
- 2차원에서의 Transform
- 각각 u, v로 변환한 후 다 더하기 때문에 느리다.
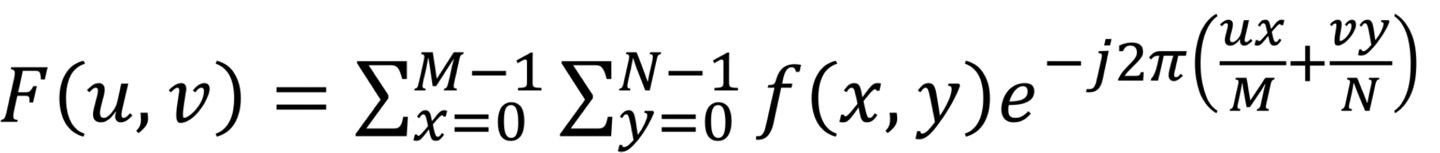
3. 2D IDFT
- 2차원에서의 Inverse Transform
- x, y로 변환한 후, MN으로 나눠서 원본 이미지를 구한다.
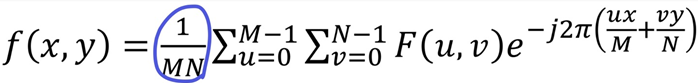
➕ 밑에서 더 자세히 다룬다
🔵 Properties of 2D DFT
❗ 𝔉[f(x, y)] = F(u, v)
- 복소수를 확인하기 위해 길이
spectrum과 각도Phase angle로 쪼개서 보자.
1. Power Spectrum
- Spectrum: 푸리에 변환으로 얻은 각 주파수 성분의 강도
F(x, y)는 복소수이고 복잡하기 때문에 크기를 확인하기 위해 각 Spectrum의 제곱한 값을 사용한다. (sin과 cos이 합쳐진 양이 얼마나 큰가~ 를 확인하기 때문에 그냥 제곱으로 확인한다.)- 실수
R과 허수I를 각각 제곱하고 더한 값이다.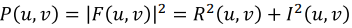
2. Phase angle
- arctan를 사용해 지수에 있는 각도를 구한다.
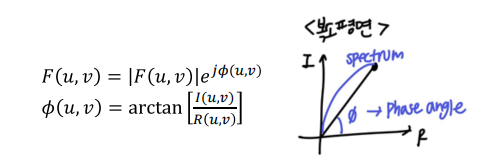
- Power Spectrum과 Phase Angle은 상호작용 관계이며, 각각 정확한 값을 알아야 Reconstruct(Inverse transform)했을 때 정확한 원본 이미지를 얻을 수 있다.
3. Translation
f(x, y)를 transform 했을 때F(μ, ν)인 상황에서 (μ-뮤, ν-뉴)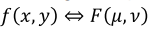
- spatial domain에서 평행이동하면 frequency domain에서는 오일러 공식으로 shift 되고,
- 그 반대면 spatial domain에서 오일러 공식으로 shift되는 것이다.
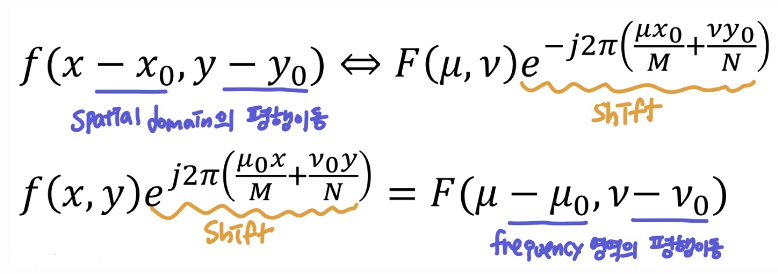
ex) Centering
- 주파수 영역에서 M/2, N/2만큼 평행이동
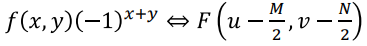
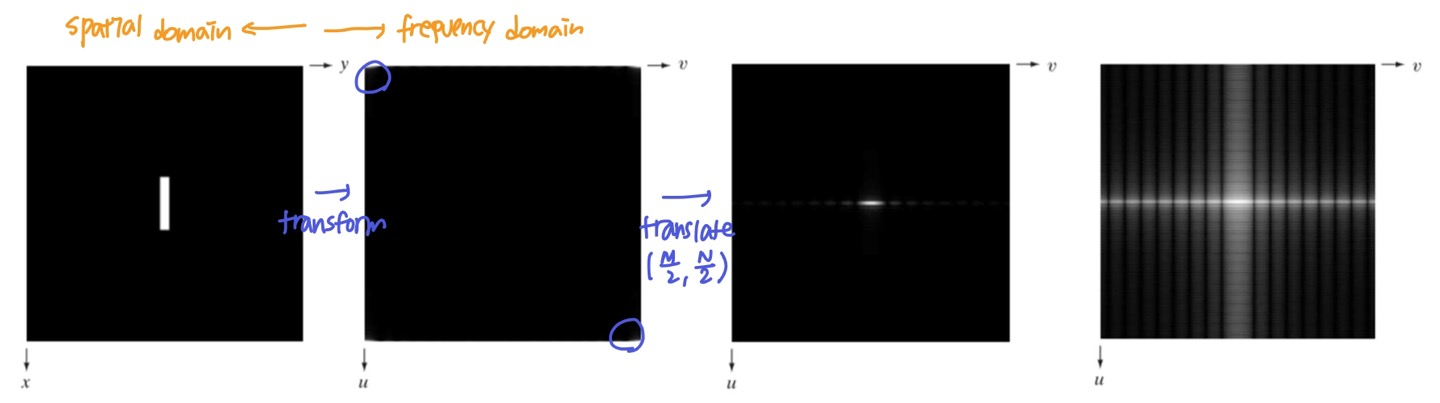
⭐ Translate는~ A영역에서 평행이동한 만큼 B영역도 평행이동 되는 것이 아니라 아예 다른 모양이 나온다.
4. Rotation
- spatial domain영역의 거리가 r, 각도가 θ인 값을 transform했을 때 frequency domain영역의 거리가 ω, 각도가 Φ인 값인 상황에서
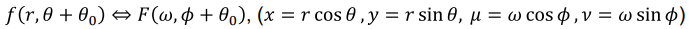
- spatial domain에서 회전하면 frequency domain에서도 동일한 각도로 회전한다.
⭐ Rotate는~ A영역에서 회전한 만큼 B영역도 회전한 모양이 나온다.
5. Convolution Theorem
- 1차원과 마찬가지로 Spatial 공간에서의 Convolution 연산은 Frequency 공간에서의 곱셈 연산이다.
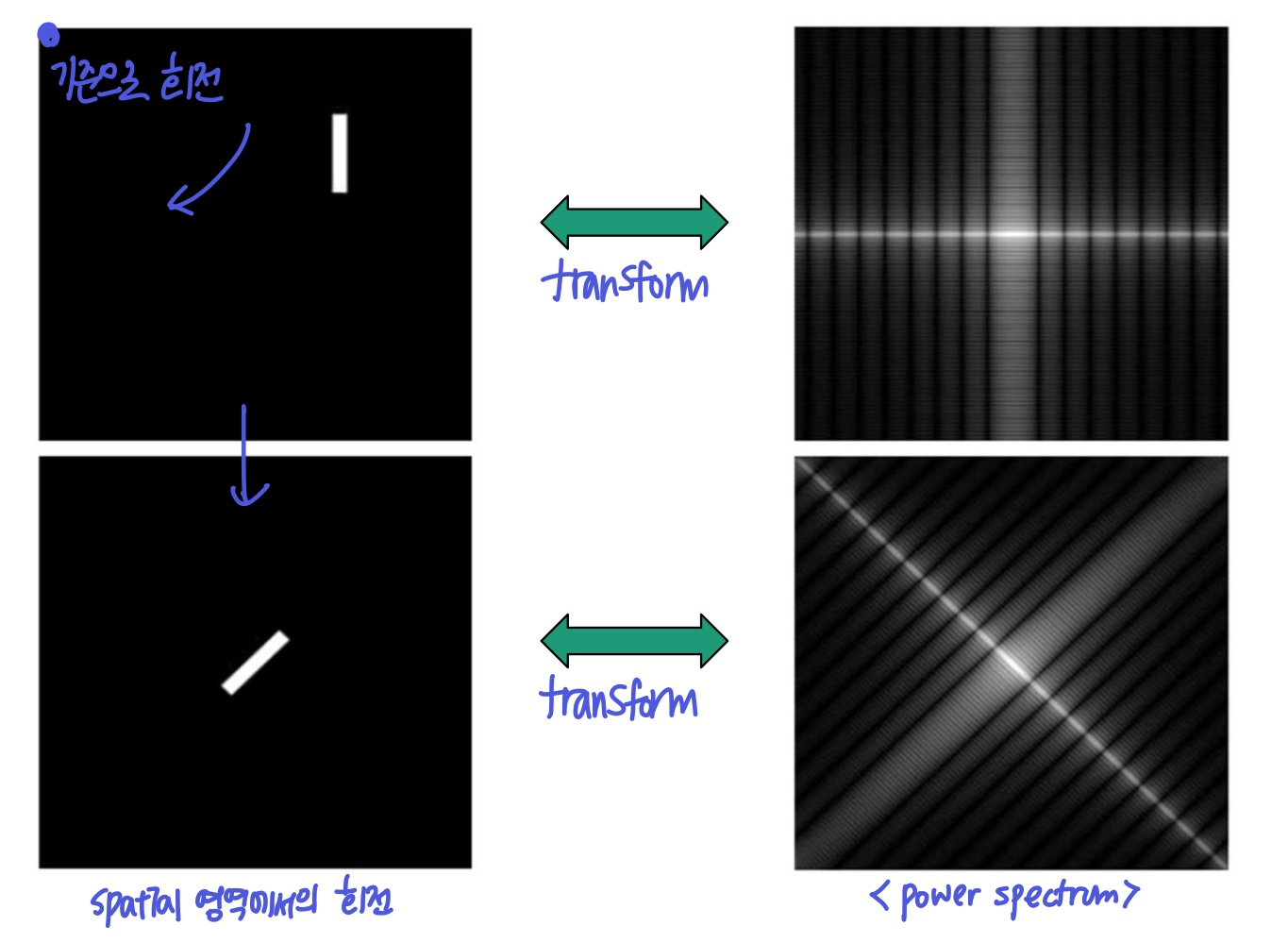
- 공간 영역에서
f와h를 Convolution하는 것은f를F로,h를H로 transform한 값을 pixel by pixel로 곱한 것과 같다.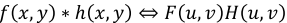
- 반대로, 주파수 영역에서
F와H를 Convolution하는 것도 마찬가지이다.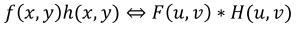
❗ 두 이미지의 크기를 서로 곱한만큼의 시간복잡도가 하나 이미지 크기만큼의 시간복잡도가 된다. 속도가 빨라짐~
6. Average value
- 공간 영역의 모든 픽셀 밝기의 평균값은 (모든 픽셀값을 더하고 MN으로 나눔) 주파수 영역의
F(0, 0)을 MN으로 나눈 것과 같다. - 주파수 영역의
F(0, 0)은 모든 픽셀 밝기의 합이다.
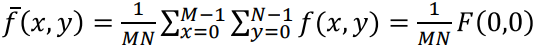

🟣 Basics of Filtering in the Frequency Domain
- Spatial domain에서 Filtering하지 말고 Frequency domain에서 Filtering하기 위한 함수
H를 만들기 H는 특정 주파수 성분의 강도를 세게하거나 약하게 하여 조절- Frequency domain에서 Filtering하고 IDFT해서 이미지 얻기
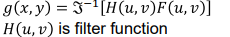
✔️ Spatial과 Frequency Domain의 관계
h(x, y),H(x, y)- Impulse response filterH(x, y)는 discrete하고 finite(범위 존재)하니까 finite impulse responce filter, FIR filter라고 불린다.- 여기서 filter는 특정한 주파수 성분만 통과시켜주는 것
- Spatial domain에서는
h(x, y)filter를 만들어서 convolution으로 필터링 - frequency domain에서는
H(u, v)filter를 만들어서 필터링
1. DC Component
- Direct current component (직류 성분)
- 주파수가 0인 자리이며(u=v=0), 전체 이미지 밝기의 평균을 나타낸다.
- 따라서, DC의 값을 조절하여 이미지의 밝기를 조절할 수 있다.
- ex) DC성분인
uv(0, 0)을 0(검정)으로 바꾸면 전체 이미지 밝기 평균이 0이 된다.
- 이미지 밝기를 조절할 때, Spatial domain에서는 모든 픽셀값을 조정해줬지만 Frequency domain에서는 한 픽셀
DC만 조정해주면 된다.
2. Low Pass Filter (Image Smoothing in Frequency Domain)
- 주파수가 낮다: 부드럽게 움직임
- 주파수가 높다: 오르락 내리락 빠르게 움직임
- 주파수가 낮은 성분만 Pass(통과) -> 이미지가 흐려진다(blur).

◾ Ideal lowpass filter
- 낮은 주파수 성분만 남기고 나머지는 0
(낮은 주파수 범위만 1을 곱하고 나머지는 0을 곱해서 없애기) D0로 범위를 조절한다. (cutoff frequency)
❗ 원점으로 부터 거리가 주파수를 나타내므로 범위는 원의 형태이다.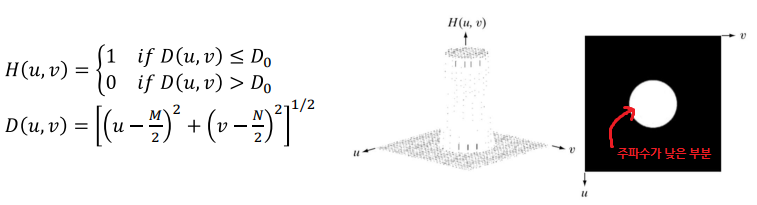

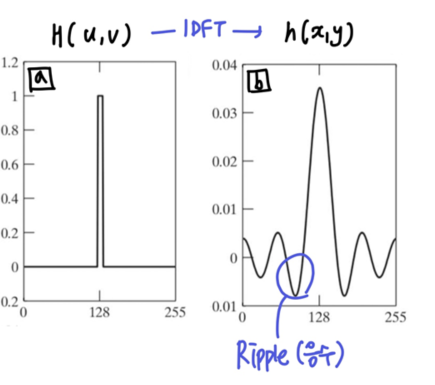
⭐ Ringing(물결파동) 현상
H(u, v)를 Inverse transform하면h(x, y)에 Ripple현상이 생기고, 이것 때문에 이미지에 Ringing 현상이 발생한다.- Ripple은 음수를 생성하며 주변이 밝으면 원본보다 더 어둡게 만든다.
a를 spatial domain의 이미지로 생각했을 때, 급격히 변하는 부분(너무 갑자기 뾰족)을 고주파 부분으로 생각할 수 있다.a를 transform하면 고주파 부분의 성분으로 인해b의 frequency domain에 Ripple이 나타난 것으로 볼 수 있다.- 이것을 해결하기 위해
H(x, y)를 부드럽게 만들어주는 Butterworth와 Gaussian을 활용한다.
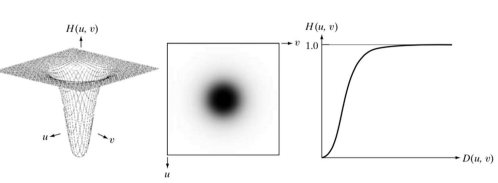
◾ Butterworth Lowpass Filters
- 아래 이미지의 식을 활용해
H(x, y)를 부드럽게 만들어서 lowpass filtering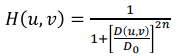


- 하지만 여전히 ripple이 생기긴 한다.
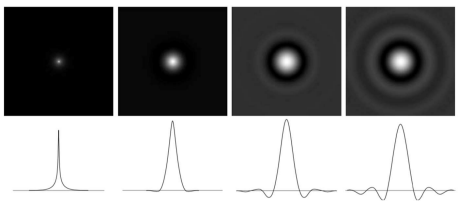
◾ Gaussian Lowpass Filters
- Gaussian은 transform해도 Gaussian의 모양을 유지하기 때문에 Ripple을 완전히 제거한다.
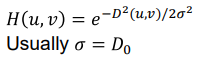

- 스캔하는 경우에도 Gaussain이 사용된다.

3. High Pass Filter (Image Sharpening in Frequency Domain)
- 주파수가 높은 성분만 Pass -> 디테일한 부분만 남겨지며 이미지가 선명해짐(Sharp)
- 높은 성분만 남기고 다 지우면 DC도 사라져서 극단적으로 디테일한 부분만 남게 되므로, DC와 주변 주파수 성분을 좀 남기기도 함 (Offsetting - 밑에 나옴)
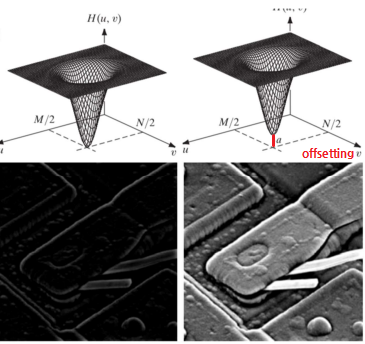
- 전체에서 주파수가 낮은 성분
HLP(u, v)을 삭제하면 높은 주파수HHP(u, v)가 남는 방식을 사용한다.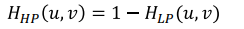
◾ Ideal highpass filters
- 높은 주파수 성분만 남기고 나머지는 0
(원점에서 먼 높은 주파수 범위만 1을 곱하고 나머지는 0을 곱해서 없애기) - D0로 범위를 조절한다. (cutoff frequency)
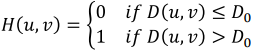
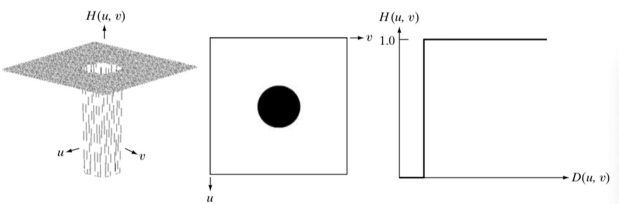
- low pass와 마찬가지로 Ringing 현상이 존재

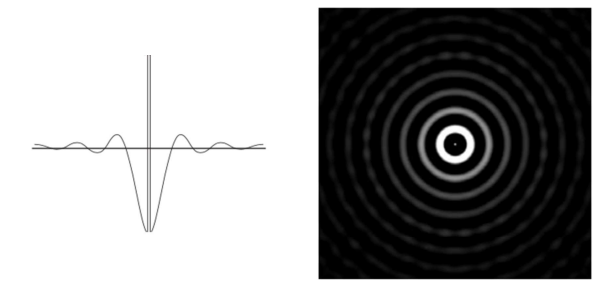
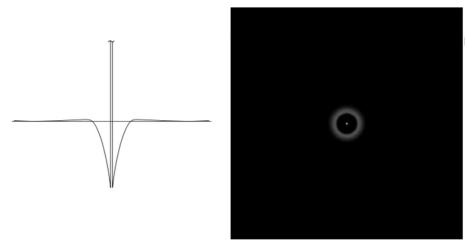
◾ Butterworth highpass filters
- 아래 이미지의 식을 활용해 H(x, y)를 부드럽게 만들어서 lowpass filtering
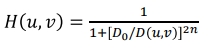

◾ Gaussian highpass filters
- Gaussian은 transform해도 Gaussian의 모양을 유지하기 때문에 Ripple을 완전히 제거한다.
- 1-Gaussian
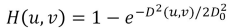

3-1. Laplacian in the Frequency Domain
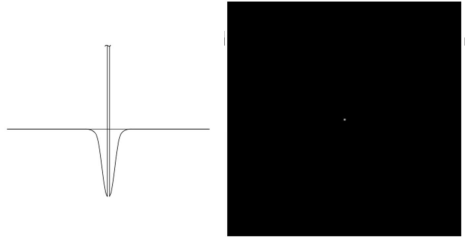
- 주파수 영역에서 2차 미분으로 구하는 Laplacian 구하기 위해 Laplacian 함수
H(u, v)를 주파수 영역인F(u, v)에 곱해 Laplacian을 구하고,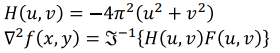
- 원본 이미지에 상수
c를 곱한 Laplacian을 더하여 선명하게 만든다. (c=1일 때 가장 잘되더라~)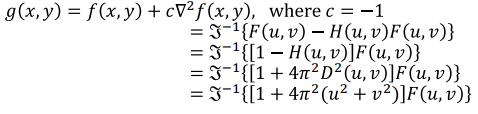

❗주파수 영역에서 Laplacain도 계산할 수 있구나~ 정도만 알기. . .
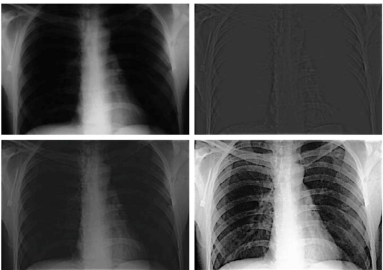
3-2. Unsharp Masking in the Frequency Domain
- 원본에서 블러이미지를 빼 세부 디테일 값을 얻는 Unsharp Masking을 주파수 영역에서 해보기
- Unsharp Mask
gmask(x, y)는 원본f(x, y)에서 lowpass filteringHLP(u, v)을 하고 IDFT를 한 이미지fLP(x, y)를 빼서 구한다. (highpass가 강조되는 mask만 남는다.)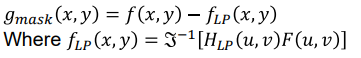
- 원본
f(x, y)에 적당한 상수k가 곱해진 Unsharp Maskgmask(x, y)를 더하여 High pass filtering을 한다.
(원본f(x, y)는 IDFT하기 전의1이다.)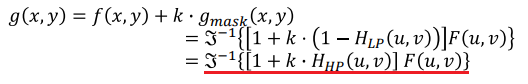
- 원본
f(x, y)인 IDFT하기 전의1을 상수k1으로 설정하면 frequency의 강도를 조절할 수 있는 filter가 된다.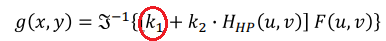
4. Homomorphic Filtering
- 빛의 영향으로 밝고 어두운 이미지

- 이미지의 밝기는 들어온 빛
i(x, y)를 얼만큼 반사하는가r(x, y)에 따라 나타난다. - 그래서 디지털 영상은 아래와 같이 표현된다.
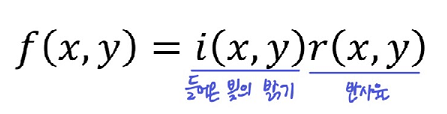
- 이때 위 식의 주파수 연산을 하기 위해 양 변을 Transform하면 곱하기 연산은 linear하지 않아 성립하지 않는다.
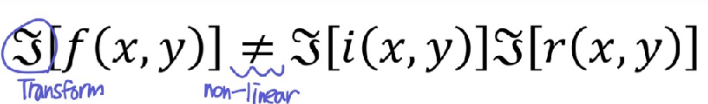
- 그래서 log를 씌워 더하기 연산 형태로 바뀔 수 있도록 하고, 그 후에 Transform을 한다. 더하기 연산이기 때문에 linear하다.
- log를 씌워 Transform한 결과
Z(u, v)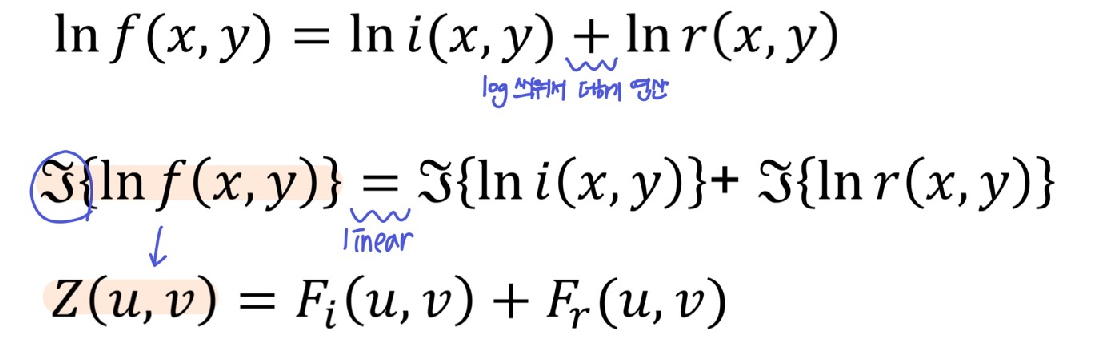
✔️ f(x, y)의 범위
f(x, y)의 범위는 [0, 1]인데, log를 씌우면 [-∞, 0]이 된다.- 이를 방지하기 위해
f에 +1을 한 [1, 2] 범위에서 log를 씌워 [0, log2]가 되도록 한다.- 다 계산한 후 마지막에 f에서 -1을 해주면 된다.
1. Filtering Z using H
Z(u, v)에H(u, v)filtering을 적용한다.- linear하기 때문에 쪼개진
Z(u, v)에 각각H(u, v)를 적용할 수 있다.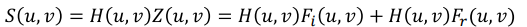
2. Back to spatial domain
- Inverse Transform을 적용한다.
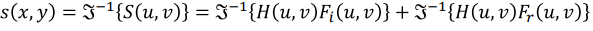
3. exponential
- log를 곱해줬었기 때문에 Exponential을 하여 되돌린다.
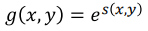

◾ Illumination-Reflectance Model H(u, v)
😬 그래서 Homomorphic Filtering이 뭔데? -> 걍 Sharpening임
HxFi가 거의 0이 되어서 (빛의 효과가 없음)HxZ=Fr이 되게 하여 reflectance를 찾는 함수H(u, v)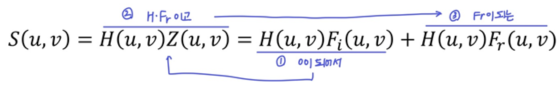
H(u, v)로 하고싶은 것은 저주파의 기여도는 줄이고, 고주파의 기여도는 높임으로써 엣지를 강조시키는 Sharpening이다.
- Illumination
i(x, y): 공간에 따라 천천히 변한다. -> 저주파- Reflectance
r(x, y): 상이한 객체가 접하는 지점에서 급격하게변한다. -> 고주파
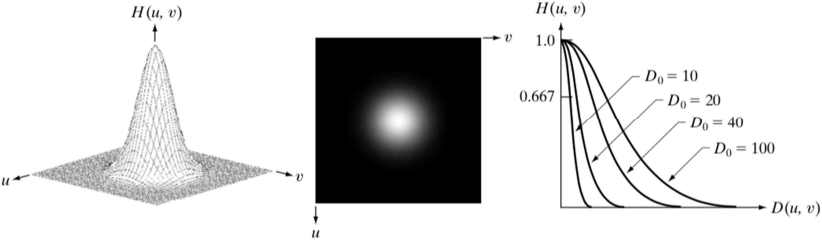
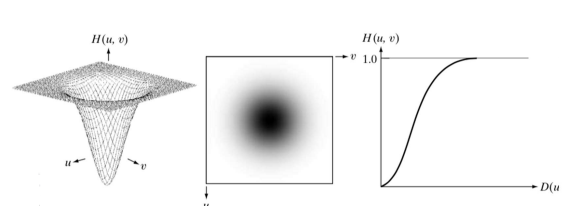
- 위의 두 저주파와 고주파 성분에 서로 다른 제어를 하여 아래 그래프처럼 저주파의 기여도는 줄이고, 고주파의 기여도는 높이기 위한 함수
H(u,v)를 만든다.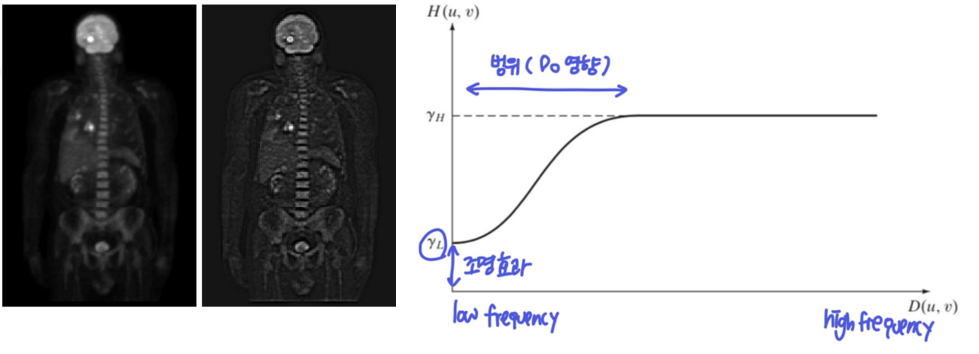
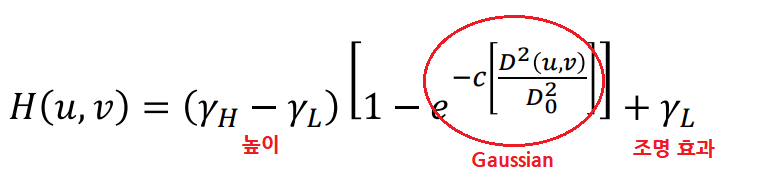
- 어쨋든 Sharpening이므로 Ringing이 생기지 않도록 Gaussian 사용
1-Gaussian
: 뒤집힌 형태의 Gaussian을 만듦D0
: Gaussian의 폭(범위)을 결정한다. low, high frequency의 정도를 조절하여 어느 정도까지 기여도를 줄일 것인지 결정한다.
->D0이 커지면 기여도를 줄일 범위가 커진다.(γH-γL)
: Gaussian앞에 곱해지며 Gaussian의 높이?를 결정한다.
->γH가 1이면 그냥 high pass filter이다.
->γH가 커지면 고주파의 기여도가 높아지며 밝음, 어두움이 더 선명하게 나타난다.γL
: 전체적으로 더해지며 조명효과를 좀 남겨두기 위한 것이다. (위에서 언급됐던 offsetting)
5. Notch Filter (Selective Filtering)
- 특정 주파수 하나만 없애기
- 또는 특정 주파수 영역~을 없애기
❗ 원점으로부터 거리가 주파수 이므로 주파수가 같은 부분은 원 형태로 나타난다.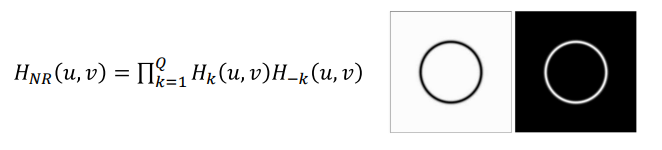
- ex1)

- ex2)








덕분에 요점 잘 파악했어요. 감사합니다.