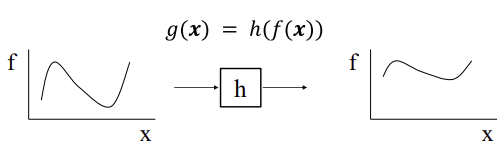
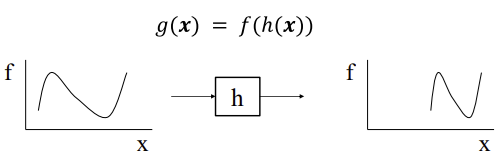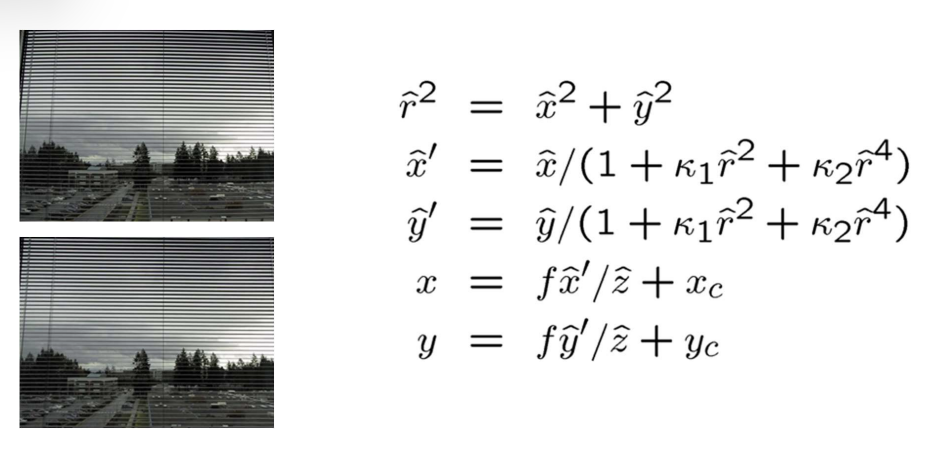Stiching
- 두 이미지의 관계를 계산하는 문제 -> 두 번째 이미지를 transform(motion model)해서 첫번째 이미지에 붙이는 과정
Image Mosaics
- 여러 개의 이미지를 경계가 안보이도록(seamless) 붙이기 ->GOAL
4. Finding relative "transformation"
- 이미지에 어떤 transformation을 해야 다른 이미지와 붙을까(같은 시점이 될까)
- 카메라(COP)의 PP에서 보이는 물체의 실제 위치 -> COP의 ray 상에 존재 -> 실제 물체의 위치가 어느 방향인지는 알 수 있음
- 방향을 알기 때문에 실제 PP에서 가상적으로 만든 Synthetic PP로 projection하면 같은 COP를 가진 다른 PP씬을 얻을 수 있음 (같은 물체의 다른 시점)
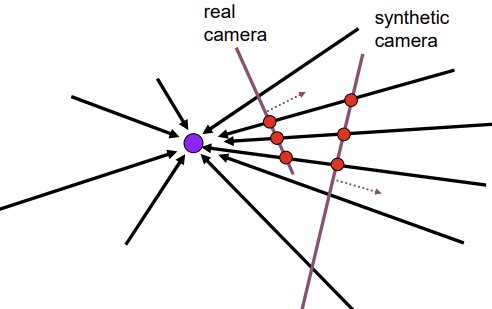
- 2D Rotation (COP가 동일한 경우)
- 다른 PP를 위와 동일한 Synthetic PP에 projection하면 위에서 얻은 새로운 PP씬과 동일한 시선의 다른 장면을 얻을 수 있음
-> 이미지가 연결되며 stitching되는 과정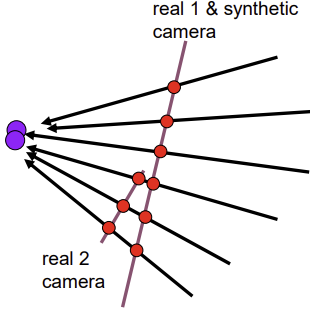
- 다른 PP를 위와 동일한 Synthetic PP에 projection하면 위에서 얻은 새로운 PP씬과 동일한 시선의 다른 장면을 얻을 수 있음
- 2D Rotation + 2D Translate (COP가 달라진 경우)
- COP가 달라져도 Synthetic PP에 projection하면 동일한 시선의 다른 장면을 얻을 수 있음
-> stitching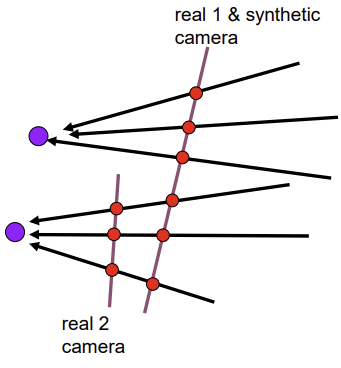
- COP가 달라져도 Synthetic PP에 projection하면 동일한 시선의 다른 장면을 얻을 수 있음
Motion model
- 두 이미지 사이에 적용되는 카메라 움직임
- 상황에 따라 적절한 motion model을 사용해야함 (2D와 3D motion model이 존재)
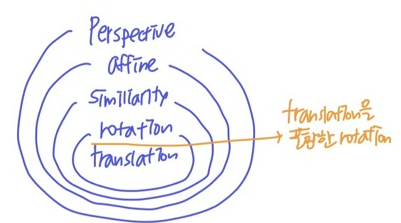
- translation, rotation, scale (similarity)
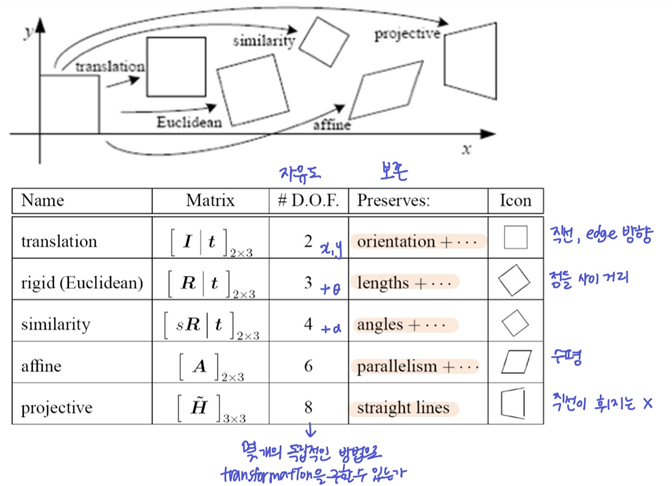
-> 각도 유지O, 평행 유지O (네 점으로 이뤄진 변 사이) - affine: 2x3으로 나타나는 모든 transformation (nonuniform; shere)
-> 각도 유지X, 평행 유지O - perspective: 이미지 상의 네 점이 독립적으로 움직이는 transform ⭐
-> 각도 유지X, 평행 유지X
-> planar scene (피사체가 평면인 경우)는 잘 적용 되지만, 평면이 아닌 경우 잘 안될 수 있음 (아래 나옴)
-> homogeneous coord에서만 정의됨
- translation, rotation, scale (similarity)
Perspective transformations
- Synthetic PP로 projection했을 때, COP에서 PP까지의 거리(focal length)가 일정한 비율로 바뀌지 않음
-> 더 많이 멀어진 부분(파란색)에서 이미지가 더 커지는데 이것은 부분적으로 이미지 크기가 변하는 것(부분적으로 거리가 변하는 것)이라 affine으로 설명되지 않음
-> Motion model: Perspective transform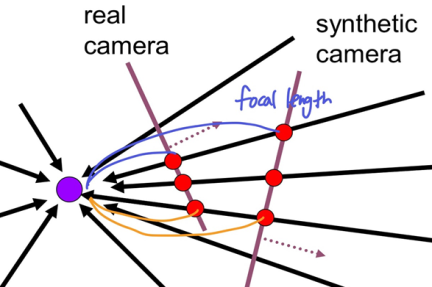
- Perspective transform으로 시점이 다른 두 카메라(PP1, PP2)에서 같은 시점의 이미지 하나(PP3)을 만들 수 있음
- 3차원 -> 2차원 transform은 무조건 Perspective transform (parallel 유지X)
- PP3->PP1, PP3->PP2은 Perspective transform이고, PP2<->PP1도 Perspective transform이다(PP1 -> PP3 -> PP2의 과정으로 2번 transform)
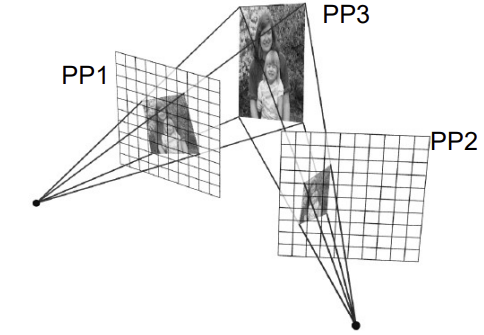
- Homographies (2차원 homography -> 2차원 homography)
- [g, h, i]에 [0, 0, 1]이 들어가면 affine, 다른 수가 들어가면 perspective
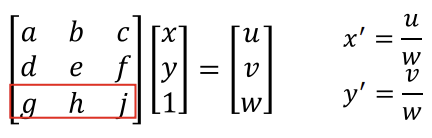
 (위 변환을 keystone distortions라고도 함)
(위 변환을 keystone distortions라고도 함)
- [g, h, i]에 [0, 0, 1]이 들어가면 affine, 다른 수가 들어가면 perspective
Nonplanar scene and Changing camera center
(planar scene에서의 perspective transformation은 사각형에서 사각형으로의 transformation이고 무조건 존재)
- 피사체가 평면이 아닌데 COP가 바뀐 경우 = 카메라의 위치가 바뀐 경우
- 각 시점의 PP를 하나의 Synthetic PP로 projection하면, 각 시점에서 다른 물체였는데 Synthetic PP에서는 같은 곳으로 투영될 수 있음
- 또는(반대로 생각했을 때), Synthetic PP에서 한 특정 위치만 나타내므로 geometric하게는 같은 부분이라 생각했는데 사실 다른 부분
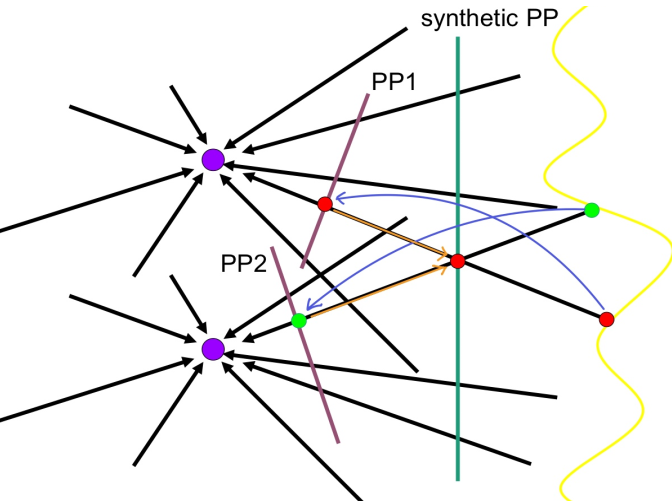
- 카메라를 움직였을 때, 보이는게 안보이게 되는 현상 -> stiching하기 어렵다
- COP가 같으면 물체 사이 관계와 ray방향이 같이서 어느곳에 projection해도 똑같이 나옴
- 하지만 COP가 바뀌면 문제가 생기고, 멀리 있는 피사체에는 COP 변화가 별로 느껴지지 않아서 큰 영향이 없지만 가까운 피사체에는 큰 차이가 나타남

- 위 이미지를 붙이고 싶다면?
- 어떤걸 기준으로 해야할까
- 나무를 기준으로 하면 집이 사라지고, 집을 기준으로 하면 나무가 2개
-> COP의 문제: 일부 정보가 사라지거나(parallax) 중복되는 문제(ghosting)
5.Image Warping
- Warping: 이미지가 transformation되었을 때, 각 픽셀들이 다른 위치로 대응
-> 이때 픽셀값은 어떻게 되는가?
- Image Filtering(Processing)
- 이미지의 밝기 값(이미지 함수의 값)을 바꿈
- change range
yof image- Image Warping
- 이미지의 공간적 위치(x방향)에 따라 바꿈
- change domain
xof image- 아래 이미지는 x방향의 scaling과 translation
Parametric(global) warping
2D Coordinate transformations
- 포함 관계를 가짐 (nested grounp)
- ex) perspetive transformation의 특이 형태 중 하나가 affine ...
1. Forward Warping
- 원래 위치
x를 trasformation해서 새로운 위치x'를 찾고, 새로운 픽셀값g(x')에 원래 픽셀값f(x)을 적용한다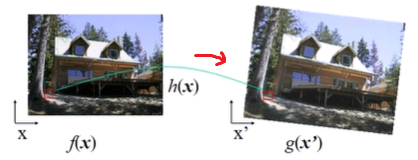
- 하지만, transformation해서 찾은 위치가 여러개의 픽셀이 겹쳐있다면?
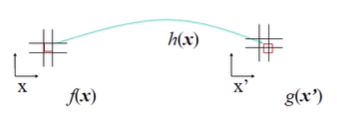
- splatting: transformation해서 찾은 위치 주변에 적당한 분포를 가진 것(Gaussian등)을 모든 픽셀에 대해 찍으면, 각 픽셀은 여러 개의 점에서 온 픽셀값을 갖게 되는데, 이러면 한 픽셀에 너무 많은 데이터를 가지게 되므로 얼만큼 찍혔는지의 값으로 나눠줌 (거의 안씀)
- 그대신 Inverse warping
2. Inverse Warping
- 새로운 위치
x'를 Inverse transformation해서 원래 위치x를 찾고, 새로운 픽셀값g(x')에 원래 픽셀값f(x)을 적용한다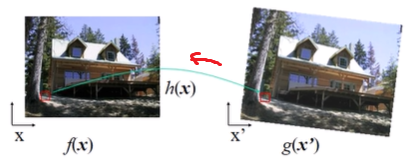
- 하지만, 이 방법도 Inverse transformation해서 찾은 위치가 여러 개의 픽셀이 겹쳐있다면?
(아래 이미지는 그리드가 겹치는 부분이 픽셀.. 인듯)
- Interpolation로
g(x')에 들어갈 유일한 색을 만든다- nearest neighbor (가장 가까운 픽셀값)
- bilinear (한 차원에서 2개의 픽셀로 보간(x, y; 총 4개), 직선)
- bicubic (한 차원에서 4개의 픽셀로 보간(x, y; 총 8개), 3차 곡선)
- sinc/FIR (sinc:
sinx/x)
- Interpolation로
Motion models for Inverse warping
- Inverse warping을 위해 두 번째 이미지에 어떤 transformation을 적용할 것인가
- 원본 이미지
빨강에 transformation한 두 번째 이미지초록를 붙이기
- 3D rotation: COP는 고정하고 3차원 상에서 PP를 rotation
- 일반적인 perspective보다 제한적인 motion model (perspective의 special case)
- 중심축 거리를 유지하며 3가지 방향(상하/좌우/각도회전)으로 독립적으로 움직일 수 있어서 자유도=3
- 3D rotation: COP는 고정하고 3차원 상에서 PP를 rotation
- Motion model을 만들기 위해 각 transformation별로 필요한 점(대응 관계)의 개수
- Translation = 자유도 2 = 점 1개
- Silmilarity = 자유도 4 = 점 2개
- Affine = 자유도 6 = 점 3개
- Homography(=Perspective=Projective) = 자유도 8 = 점 4개 (결국 사각형->사각형이므로)
2-1. Plane Perspective mosaics
- translation, Affine으로는 이미지가 잘 붙을 수 없으므로 minimun perspective를 해야함
- 4개의 점을 알아내서 8개의 파라미터로 푸는 3x3 Homogenouse transform 계산 문제
- 한계 (그래서 대신 rotational mosaics를 사용하기도 함)
- local minima: 4개의 점 중 더 정확한 점이 있음에도 불구하고 local에서만 정확한 점을 찾아내서 결국 정확한 점을 얻지 못함
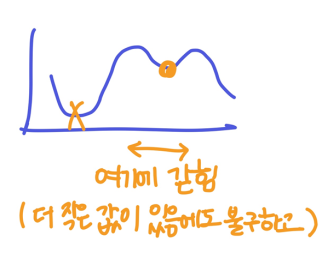
- slow convergence: match를 하면 4개가 아닌 여러개의 점이 나오므로, 최적의 값을 찾기 위해 차근차근 계산해나가므로 convergence(수렴)과정이 느림
- 여러 개의 점(match)중에 4개를 어떻게 고를까
-> numerical optimization: 더 좋아지는 방향이 없을 때까지 transformation을 반복 - 하지만 이것도 local minima처럼 전체함수가 아니기 때문에 더 좋은 방향이 있음에도 찾지 못하 경우가 존재![]
- 여러 개의 점(match)중에 4개를 어떻게 고를까
- difficult to control interactively
- 잘못된 점을 수정하려면 8개의 매개변수가 있는 행렬을 수정해야되는데 어려움, 직관적이지 않음 (교수님 생각은 아니시다..)
- local minima: 4개의 점 중 더 정확한 점이 있음에도 불구하고 local에서만 정확한 점을 찾아내서 결국 정확한 점을 얻지 못함
Perspective Projection Model (3D -> 2D)
- (Extrinsics) world coord
X, Y, Z에서 transform해서 camera coordXc, Yc, Zc로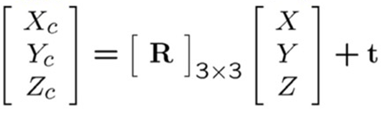
- (Intrinsics) camera coord
Xc, Yc, Zc에서 transform해서 screen coordu, v, 1로
Camera coordinate
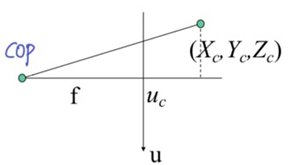
2-2. (3D) Rotational mosaics ⭐
- Perspective model의 special case -> 결과적으로 homography 계산
- COP가 고정되어있다고 볼 때, pp를 움직임 (찍을 때 카메라가 움직였다는 것은 pp가 움직인 것 이므로)
- COP가 고정된 경우는 rotation만으로도 충분하므로(자유도 3), perspective와 비교했을 때, 5개의 자유도가 쓸데없음 (오히려 이 5개 때문에 더 망가지는 걸 방지)
- 장점
- ability to build full-view panoramas: 360도 커버 가능
- easier to control interactively: 직관적인 3개 매개변수만 존재 (회전, 상하, 좌우 이동은 마치 translation과 rotation처럼 보이지만 결과는 3D 상에서)
- more stable and accurate estimates: 계산 좀 더 간단
(3D) Rotational Projection Model
- 이미지의 한 점을 3D ray로 pp에 투영
- pp위 한 점의 3차원 좌표(world coord)
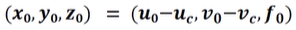
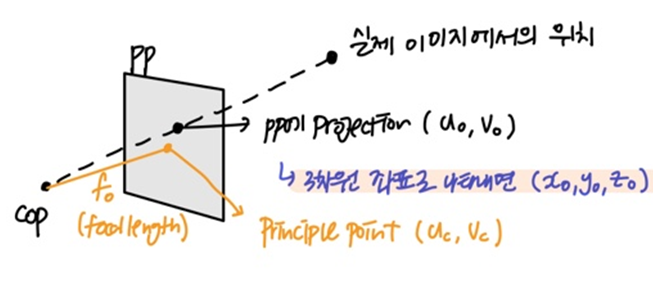
- pp위 한 점의 3차원 좌표(world coord)
- 카메라 모션에 따라 rotation (ray가 rotation)
- rotation된 점의 좌표
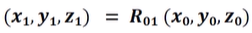
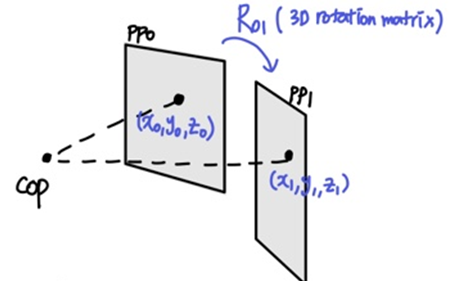
- rotation된 점의 좌표
- 원래 이미지로 다시 projection
- PP1에서의 점이 PP0에서 어디서 나타나는지를 알면 PP1에서의 점의 2차원 좌표
u1, v1를 알 수 있음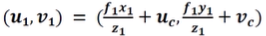
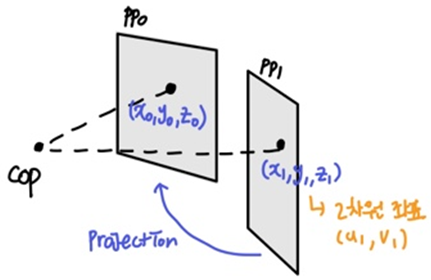
- PP1에서의 점이 PP0에서 어디서 나타나는지를 알면 PP1에서의 점의 2차원 좌표
▪️ Cylinder Panomara ⭐
Image Mosaic
- Mosaic을 만들기 위해 같은 부분 찾을 때
- Direct Method: use generalization of affine motion model
- Feature-based Method: Feature를 찾고, match해서 R 계산 (보통 이거 사용)
360º field of view
- 문제: 사이드가 늘어나는 현상
- 정면: 카메라로부터 물체의 depth(z)가 큼, 큰 z로 나눠서 작게보임
- 사이드: 정면과 동일한 pp로 projection시키면 z가 짧아짐 (좌우를 찍은 것은 카메라를 돌려 찍은 것으로 z축이 바뀐 상태인데, 이 z축을 강제로 정면 방향으로 돌리면서 짧아짐), 작은 z로 나누면 크게 보이고 늘어나는 현상이 나타남
- 사실 위에 사이드 설명이랑 그림은 내 추측이고, 3D rotation이 90도에 가까워질 수록 z가 0에 가까워진다, 그래서 z로 나누면 값이 커지면서 사이드가 늘나는 것
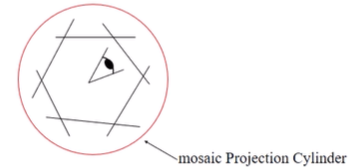
- 그래서 한 평면 PP에 투영하지 말고, Cylinder에 투영해서 투영하고난 뒤에도 모든 방향에 대해 z값이 일정하도록! (z방향만 바뀜)
- Cylinder면이 PP이므로 찍은 사진들을 알맞게 PP에 투영 하고, 겹쳐진 부분은 blend, 실린더 한 부분을 자르고 펼쳐 결과를 얻음
- 이미지를 보고 ray를 알 수 있고, ray와 cylinder의 교점에 픽셀값을 넣기 위해 cylinder에서 이미지로 projection하는 Inverse warping
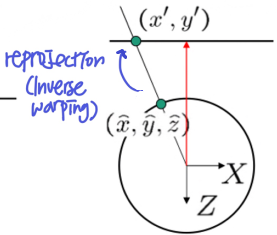
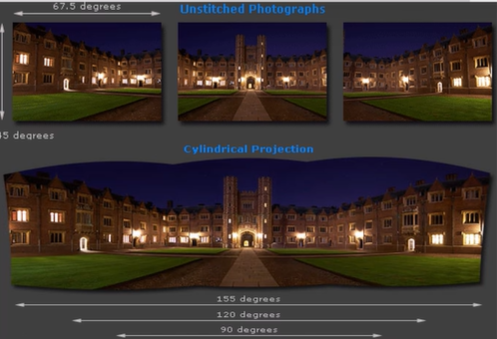
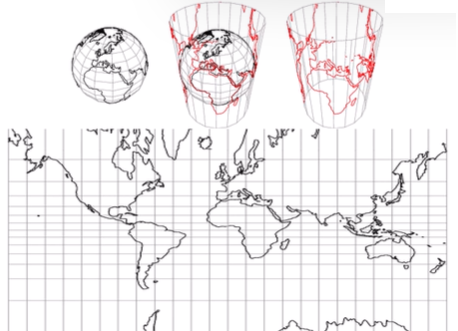
- 하지만 이미지가 휘거나, 위/아래가 늘어난다는 단점 존재
- 이미지가 휘어서 넓어지는 걸 방지한 것도 맞음
Cylinder model with focal length
- focal length에 따라 다른 실린더 매핑 결과 (Inverse warping 결과)
- focal length가 짧음 -> 화각 커짐(광각렌즈) -> ray가 크게 벌어져 실린더의 정면 입장에서 먼 곳에 투영 됨 (벡터 방향이 principle point와 멀어짐) -> 가운데 중심으로 좌우 폭이 차이가 큼 -> 넓은 폭의 곡선이 사용되므로 가장자리가 줄어듦
- focal length가 긺 -> 화각 작아짐(망원렌즈) -> ray가 약간만 벌어져 실린더의 정면 입장에서 가까운 곳에 투영 됨 (벡터 방향이 principle point와 가까워짐) -> 가운데 중심으로 좌우 폭이 차이가 적음 -> 좁은 폭의 곡선이 사용되므로 (거의 직선) 거의 줄어들지 않고 그대로
focal length 화각 폭 가장자리 렌즈 짧음 큼 넓음 줄어듦 광각렌즈 긺 작음 좁음 거의 그대로 망원렌즈 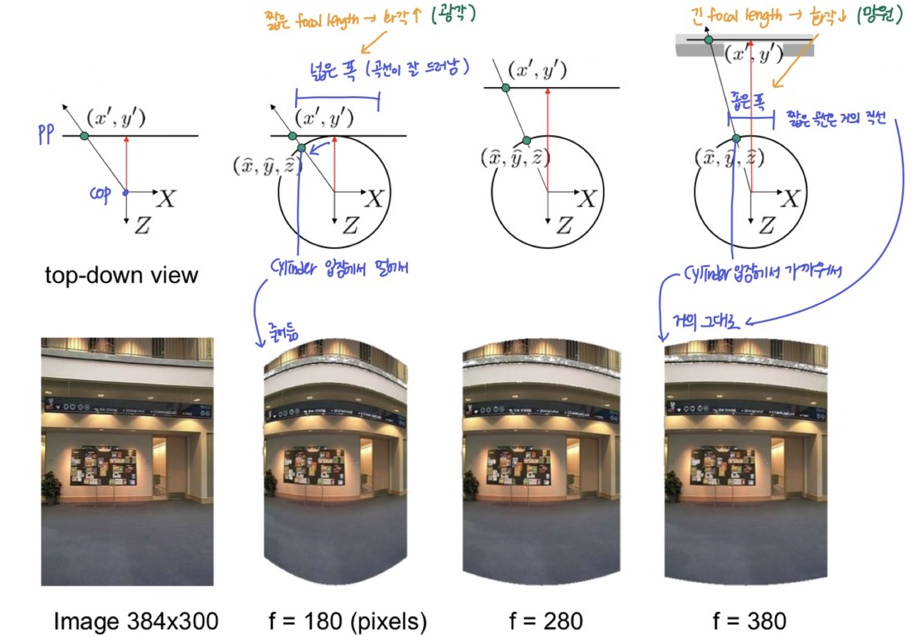
- 이미지의 같은 점을 sampling했지만 벡터의 방향만 바뀜 (principle point와 가까워지거나 멀어지거나)
- focal length는 픽셀 단위: pp의 픽셀단위로 나타낸 cop와 pp의 거리
- 고해상도 -> 작은 픽셀 -> focal length가 늘어남 (물리적으로는 변화X)
- focal length의 의미
- pp와 cop의 거리가 바뀌며 화각이 바뀌고, 이로인해 cylinder에서 나타내야할 영역의 폭이 변화되는데 pp는 일정해서 실린더의 모양이 바뀜 (폭이 넓어졌다면 일정한 pp안에 욱여넣느라 줄어드는 것)
- 결국 cylindrical model을 만들기 위해서는 focal length를 알아야하고, "pp를 어디에 둘 것인가" = "focal length의 길이를 어떻게 할 것인가"를 따져야함
(cylinder의 크기는 상관X)
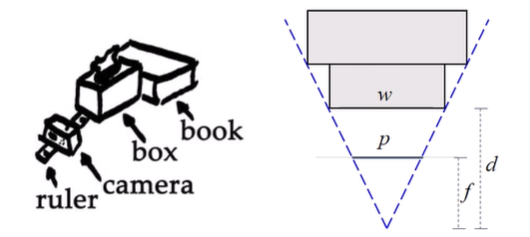
determine focal length
- 카메라의 EXIF 정보 사용 (카메라 렌즈, 노출값 등 정보)
- tape measure (줄자) 사용
- 카메라 앞에 박스 두개를 두고, 각 모서리가 일치할 때까지 카메라 위치를 조정
- 닮음 또는 각도를 활용해 알아낼 수 있음 (길이는 해상도나 센서에 따라 달라질 수 있어서 각도로 많이 구함)
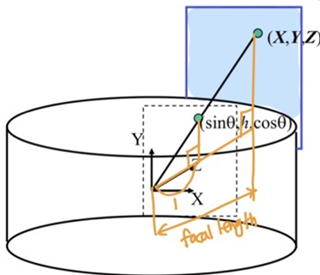
1. Cylindrical projection
- world coord
X, Y, Z를 반지름이 1인 Unit Cylinder로 projection(Map)x^, y^, z^- world coord의 점을 world coord의 xz평면 거리로 나누면 반지름이 1인 cylinder에 투영됨
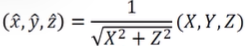
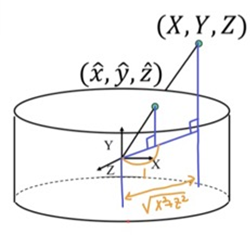
- world coord의 점을 world coord의 xz평면 거리로 나누면 반지름이 1인 cylinder에 투영됨
- 투영된 점을 높이
h와 z축으로부터의 각도θ으로 cylinder coord로 나타낼 수 있으므로,x^, y^, z^로h와θ를 알아냄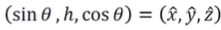
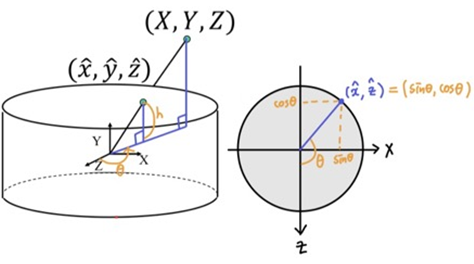
- z축을 기준으로 잘라서 펼친 unwrapped cylinder의 중심은 principal point
xc, yc이고, cylinder coord (h,θ)로 나타냄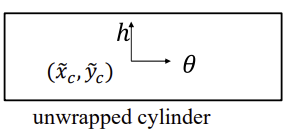
- cylinder coord를 cylindrical image coord로 변환
s: 이미지의 크기와 비례하는 어떤 값(scale)으로 unwrapped cylinder의 가로 길이가 2pi가 되도록 하는 값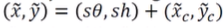

2. Cylindrical warping (Inverse warping)
- 위의 projection 과정을 거꾸로
- 알아야하는 것: focal length
f, image centerxc, yc
- cylindrical image위의 점
xcyl, ycyl로h와θ를 구함- focal length는 위 projection 과정의
s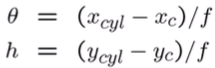
- focal length는 위 projection 과정의
h와θ로 cylinder 위의 점x^, y^, z^을 구함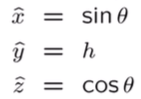
- cylinder로 projection된 점의 2차원 좌표는
x^/z^, y^/z^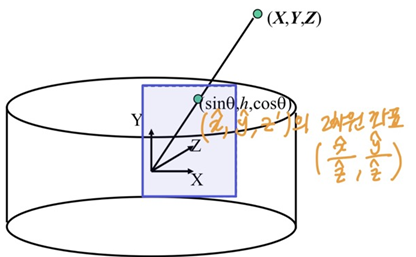
- world coord에서의 2차원 좌표 (실제 이미지에서의 좌표)
- cylinder의 반지름 길이가 1이고, pp까지의 거리가
f이므로f를 곱하고 principle point만큼 더함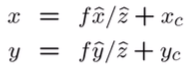
- cylinder의 반지름 길이가 1이고, pp까지의 거리가
- 한계: 천장의 이미지를 모델링할 수 없음
-> sol: Spherical warping
+) Spherical warping
- 극좌표계를 사용해 반지름이 1인 구에 projection (각도가 2개 사용됨)
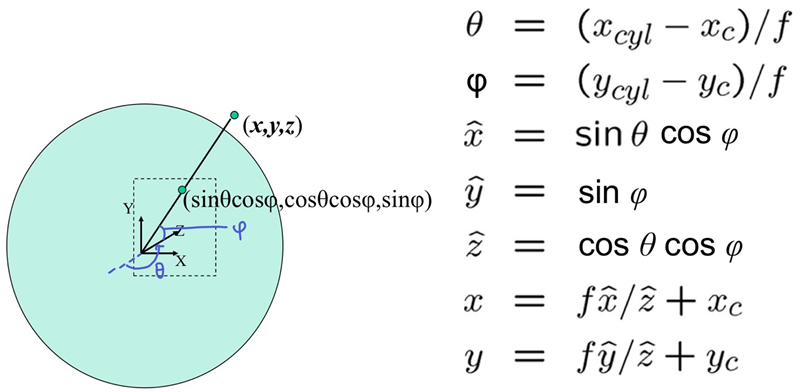 (아래 full-view panorama에서 다시 언급됨)
(아래 full-view panorama에서 다시 언급됨)
Radial distortion Problem
- 그럼에도 불구하고 이미지가 잘 붙지 않는 이유
-> Radial distortion: 렌즈 문제 때문에 가장자리의 휘어지는 현상이 발생하기도 함 (구면 렌즈로 만들어져서 생기는 왜곡 현상)- 렌즈의 중앙부와 바깥영역의 굴절률이 달라서 생기는 문제로, 방사상 모양으로 왜곡됨 (CV-02에 필기)
- Radial distortion는 ISP과정에서 보완되며, 보완되기 위해 패턴을 알아야 함
- principle point를 원점으로 하는 좌표
x, y를 사용해 구한 거리를 사용해 복원하는 식을 만듦κ는 checker board와 같은 이미 알고 있는 패턴으로 알아내는 역의 매개변수
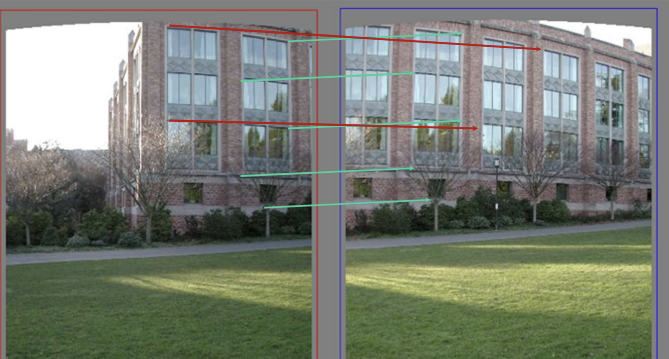
3. Image Stitching in cylinder model
- 서로 다른 이미지의 cylinder model들은 cylinder 입장에서 x방향 따라서 움직인 것 뿐 (θ만 움직임)
- 일정한 COP에서 바라보는 방향만 다르고 rotation, scale변화는 X -> 결국 x축으로의 translation만 있음
-> camera pan(고정된 위치에서 수평으로 회전만하는 기법) ↔ translation on cylinder
-> 3D rotation을 translation으로 풀 수 있게 됨
- cylinder model의 features를 매칭해서 translation을 계산
▪️ RANSAC (RANdom SAmple Consensus)
Outlier problem of computing translation
- Matching features로 Trnaslation을 계산하기 위해, 여러개의 matching의 대표값을 찾는데,
- 잘못된 matching이 존재한다면? = false positive = outlier
-> 평균은 error의 min square를 찾는 것이기 때문에 outlier에 굉장히 민감
-> sol: RASAC
- 필요한 Transformation에 따라 Feature pairs를 랜덤으로 고르고 transformation 계산
ex) 4개의 feature pairs로 homograpyH계산 - 가장 동의를 많이 받은 것으로 선정 (Consensus:의견일치, 합의)
Line Fitting
- 점들이 나타내는 직선 찾기
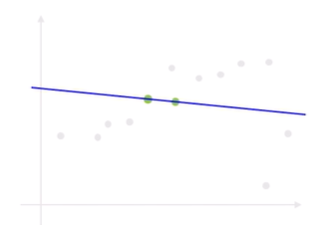
- Least squares line(평균)
- 아래 2개의 outliers 때문에 큰 영향을 받아 아래쪽으로 쏠린 line

- 아래 2개의 outliers 때문에 큰 영향을 받아 아래쪽으로 쏠린 line
- RANSAC
- random sample로 model 만들기: (Line을 그리기 위해 점 2개가 필요하므로) 랜덤으로 점 2개 sampling한 뒤 Line 그림
- Consensus: 그 line에 들어가는 점(=Inlier)은 해당 모델에 투표 (x값을 직선에 넣었을 때 y범위 안에 sample이 들어오면)

- 반복하면서 동의를 가장 많이 받은 line이 RANSAC line (= lnliers가 가장 많은 line)
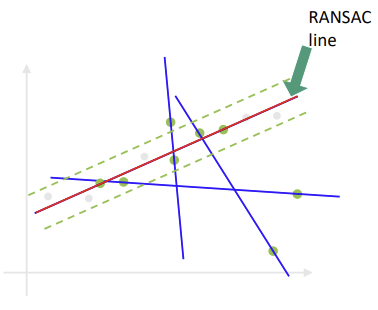
- random sample로 model 만들기: (Line을 그리기 위해 점 2개가 필요하므로) 랜덤으로 점 2개 sampling한 뒤 Line 그림
▪️ Alignment
- stiching된 이미지들의 오류를 보완하는 방법
1. Drift problem
- 작은 (vertical) 에러들이 쌓여서 축적되어 생기는 문제 (튀어나온 부분들을 자른다고해서 해결될 문제가 아님)
- 처음에 비뚤어지게 사진을 찍었는데, 똑바르게 찍었다 생각하고 수평으로 이동한 경우(비뚤어진 상태로 비뚤어지게 이동)
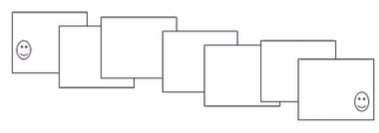
- Cylinder 모델이기 때문에 끝과 끝을 이어서 360도(360º pan)가 되어야하는데 부족하거나 넘어가는 경우
- 이유1: 각 이미지들은 카메라가 고정되어있다고 가정되어있기 때문에 3D rotation model을 사용해서 붙이는데, 실제로는 절대적으로 카메라가 고정될 수 없으며 약간의 translation만으로도 에러가 발생할 수 있음
- 이유2: 알고있는 focal length와 실제 focal length가 안맞음
- [초점을 맞출 때 줌인/줌아웃 = focal length 바뀜 = cylinder에서 한 이미지가 차지하는 영역이 바뀜] -> 을 고려하지 않아서
- 처음에 비뚤어지게 사진을 찍었는데, 똑바르게 찍었다 생각하고 수평으로 이동한 경우(비뚤어진 상태로 비뚤어지게 이동)
Solution
- Piece-wise (책의 고전적인 방법)
- 첫번째 이미지와 마지막 이미지를 붙이기 위해 마지막 이미지의 복사본을 30pixel 위로 이동시킴
- 그 사이 이미지가 10개 있다면, 마지막에서 두번째 이미지는 27pixel 올리고, 마지막에서 세번째 이미지는 24pixel 올리고... -> Error distribution
- Bundle Adjustment ⭐
- stiching 과정에서 2장 사이의 관계만 보고 붙이는 것이 아닌, 전체적인 모습을 보며 한번에 stiching
- 전체 이미지의 parameter를 동시에 조절하며 맞을 때까지 -> 덩어리가 큰 수치적 최적화 문제
- 복잡하고 시간이 오래 걸리지만 많이 사용됨
- 교수님의 방법...
- 비뚤어지게 사진을 찍었다면,, 돌리기
- 360도가 안된다면,, focal length 조절해서 한 장이 차지하는 영역 늘리기 (focal length가 짧아지면 이미지 확대)
2. Problem of Full-view (360º spherical) Panoramas
- spherical mapping
- 곡면을 가지기 때문에 panorama가 휘어보이는데, 천장 부분은 극단적으로 이상하게 늘어나있음
-> 극점에 있는 점은 실제로는 1개인데, 구를 펼치면 line 전체를 커버해야되기 때문
- 곡면을 가지기 때문에 panorama가 휘어보이는데, 천장 부분은 극단적으로 이상하게 늘어나있음
- Sol: Cube mapping
- 직선이 거의 휘지 않고, 크기 왜곡이 적음
- 하지만 edge에서 직선이 꺾이는 현상이 나타남 (이걸 약간씩 휘어둔게 spherical..)

Solution
- 어떤 사진이 어떤 사진들과 매칭되야하는지 다 고려
- 3D rotation model 사용
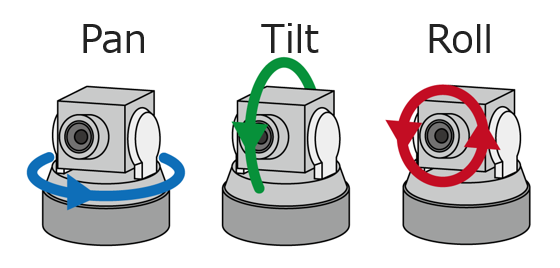
- 이러한 문제는 pan, tilt, roll이 다 되는 것을 고려해야하기 때문 (Drift는 pan만 고려)
- 모든 쌍들끼리 feature based match를 해서 이전 match를 보고 다음 match를 결정하는 점진적인 방법을 쓰거나, bundle adjustment⭐ 처럼 전체적으로 해결하는 방법을 쓰기도 함
✔️ Camera Pan, Tilt, Roll
✔️ Bundle adjustment는 drift와 360º panoramas에 다 적용될 수 있음
▪️ Recognizing Panoramas
- 사람이 control해서 찍은 이미지들을 붙이는 것이 아닌, 무작위한 사진들을 붙여야 할 때
-> 어떤 부분이 어딘지를 알아내야함
- feature point matching으로 겹쳐야하는 이미지 알아냄
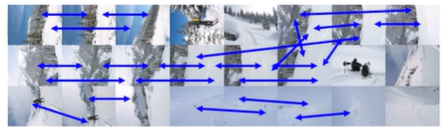
- 각 사진들을 node라고 보고, 연결된 사진들끼리(=충분한 수의 공통된 feature를 가진 사진들) match해서 graph 생성
- graph에서 Connected component 찾아 group 생성
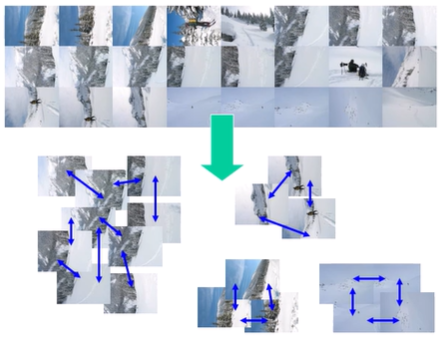
- group끼리 matching하고 piece-wise 또는 bundle adjustment해서 stiching!

지금까지의 방법은.. 아직도 5-10%의 실패율을 가짐.. 그 이유는 아래에..
▪️ Matching Mistakes
local feature의 한계 -> False positive
- 전체적으로는 다른 부분인데, 부분적으로 보니 같아서 같은 feature로 인식
- 잘못됨을 인지하기 어려움


False Negative
- 찾을 수 있는데 못 찾은 경우
- 그림자, 피사체의 움직임, parallax 등..

low overlap & "feature-less" region
- 겹치는 부분이 적거나 알아차리기 힘든 경우

이러한 문제들은
- 같은, 비슷한 부분이 반복되게해서 이상한 alignment를 하거나, alignment를 실패하게함
solution
- feature detector, feature matcher, RANSAC, verification stage를 강화..(튜닝)
- Higher-level knowledge 사용
- feature point matching으로 찾기 어려운 부분을 찾기 위해
- local feature 사용하기 전에 딥러닝을 사용하거나 또는 사람이 직접 알려주는 방법으로 미리 match될 부분, 안 될 부분 구분
- 카메라 모션을 사람이 직접 알려주거나, 센서를 사용해 알아내기 (중력가속도, 각가속도 센서)
- ex) 파노라마를 찍을 때, 센서를 사용해서 적당한 overlap(겹치는 부분)을 가지고 수평으로 잘 이동하면 자동으로 찍어주는 기능
7. Image Blending
Image Feathering
- 이미지가 붙는 경계를 자연스럽게 섞어주기
- 각 이미지에 적용될 weight map 생성하고 각 픽셀에 weight를 적용한 뒤 이미지를 붙임 (삼각형 1개가 이미지 1개)

- 전체 weights의 합이 1이 안되면, weight를 모든 weights의 합으로 나눠서 1로 만듦

- weight를 적용한 두 이미지를 합쳐서 전체 weight가 1이 되도록
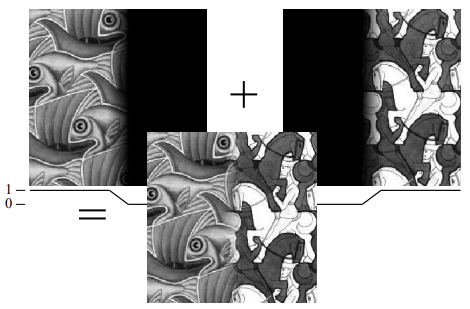
- 각 이미지의 weight 차이(간격)이 큰 것은 = window 사이즈가 큰 것
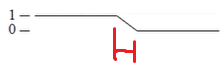
- window 사이즈가 너무 크면 ghosting
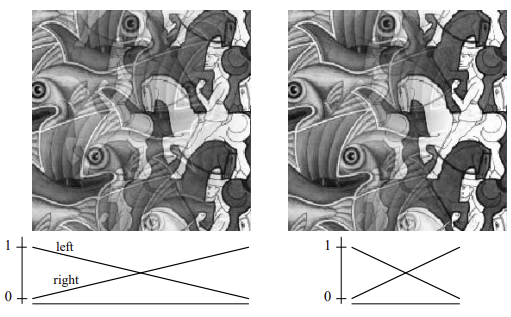
- window 사이즈가 너무 작으면 경계(seam)가 보임
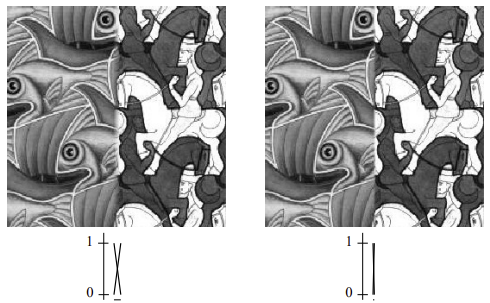
- window 사이즈가 너무 크면 ghosting
- 최적의(Optimal) window 크기를 찾기 위해 Multi scale blending 사용 (매번 결정하기 어려우니까)
1. Laplacian Pyramid Image Blending
- 이미지의 high freq 부분은 ghosting이 나오기 쉬우므로 window 크기를 줄이고, -> 거의 안뭉개
- low freq 부분은 밝기 변화 등이 잘 보여 seam이 보이기 쉬우므로 window 크기를 키움 -> 많이 뭉개
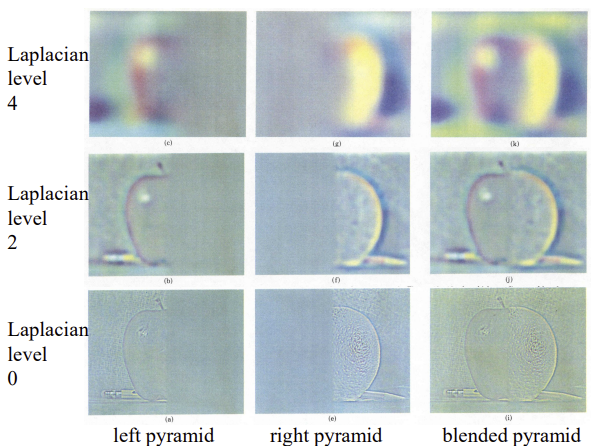
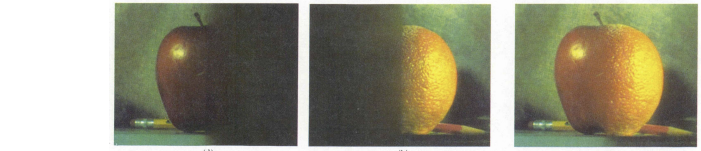
2. Poisson Image Editing
- 다른 이미지에서 따온 개, 사람 이미지의 미분값(gradient)만 살리고, 경계부분에서 boundary condition을 잡고 poisson 방정식 풀이

3. De-Ghosting
- 중앙 정장입은 남자의 뒷모습 -> 남자의 모습이 다 나오게 찍힌 이미지와 남자가 존재하지 않지만 상체 위로만 찍힌 배경 이미지가 겹친 부분
- 남자를 없앨 수 있는 방법이 없으므로 남자의 형태만 잘라서 배경 이미지에 붙임

4. Local alignment (De-ghosting)
- 작은 translation이 나타난 이미지
- 픽셀별로 warping...해서 강제로 맞춘다 ?? ㅁㄹㄹ

- 거리가 달라서 붙기 어려운게 붙을 수 있음

5. Cutout-based compositing
- 이미지를 잘라 붙일 때 가장 표 안나게 자르는 법을 계산 (최적의 방법을 찾아주는 알고리즘)
- 붙일 때 poisson을 풀어서 경계를 자연스럽게