어떤 리스트에서 이분탐색을 이용해서 특정 값을 찾을때, 리스트가 중복된 값을 포함하고 있을 수 있다. 그 중복값을 전부 찾거나 또한 그 중복값들을 활용해서 문제를 해결하는 문제를 위해서 upper_bound나 lower_bound가 존재한다.
역시나 마찬가지로 이 함수는 c++의 Algorithm.h 헤더에서 제공해준다. 이를 참고해서 java에서 구현해보도록 하자.
lower_bound
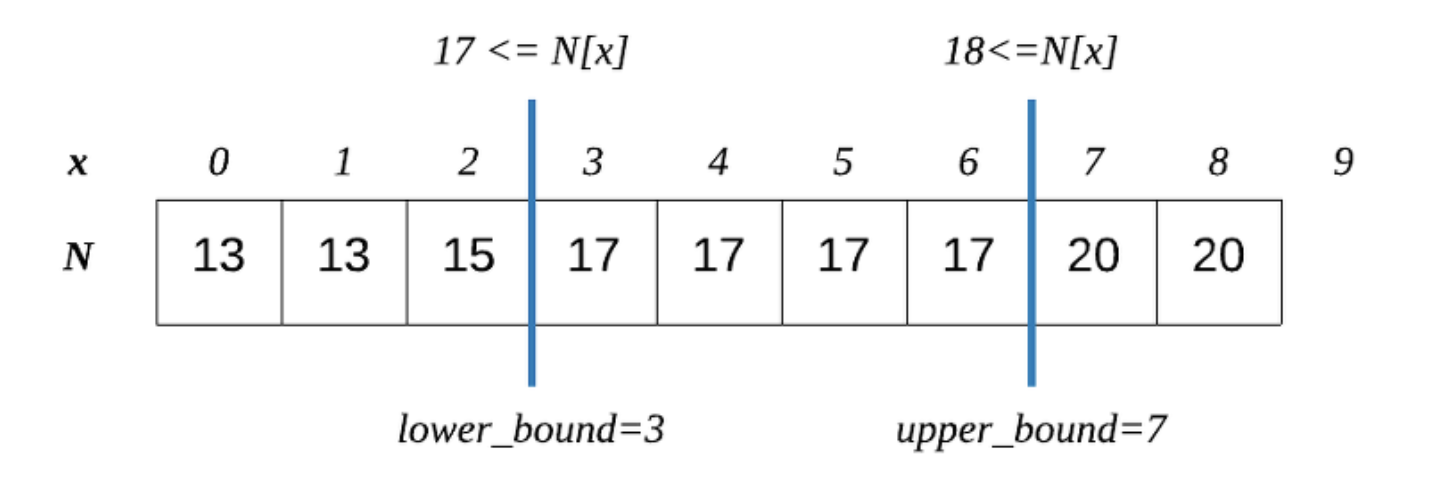
범위 [begin, end) 안의 원소들 중, 특정 target보다 크거나 같은 첫번째 원소의 인덱스를 리턴한다. 만약 그런 원소가 없다면 end 인덱스를 리턴한다.
이때 리스트는 모두 정렬된 상태여야 한다. 즉, lower_bound가 성립하기 위해서는 각각의 요소들중 element < target를 만족하는 요소들은 만족하지 않는 요소들보다 앞에 있어야한다.
c++의 lower_bound를 확인해보면 아래와같이 구성되어있다.
template <class ForwardIt, class T>
ForwardIt lower_bound(ForwardIt first, ForwardIt last, const T& value);인자로 (리스트의 시작, 리스트의 끝, 찾고자하는 값)을 받고있다. 그리고 앞에서 언급했다시피 리턴값은 찾고자하는 값의 첫번째 인덱스를 리턴하기 때문에, 고려해서 java로 작성해보자.
구현
private static int lowerBound(List<Integer> data, int target) {
int begin = 0;
int end = data.size();
while(begin < end) {
int mid = (begin + end) / 2;
if(data.get(mid) >= target) {
end = mid;
}
else {
begin = mid + 1;
}
}
return end;
}upper_bound
범위 [begin, end) 안의 원소들 중, 특정 target보다 큰 첫번째 원소의 인덱스를 리턴한다. 만약 그런 원소가 없다면 end 인덱스를 리턴한다.
이때 리스트는 모두 정렬된 상태여야 한다. 즉, upper_bound가 성립하기 위해서는 각각의 요소들중 element <= target를 만족하는 요소들은 만족하지 않는 요소들보다 앞에 있어야한다. lower_bound와 비교해보면 등호가 들어가는데, target보다 큰 인덱스를 구하기 위해서이다.
c++의 upper_bound를 확인해보면 아래와같이 구성되어있다.
template <class ForwardIt, class T>
ForwardIt upper_bound(ForwardIt first, ForwardIt last, const T& value);인자로 (리스트의 시작, 리스트의 끝, 찾고자하는 값)을 받고있다. 그리고 앞에서 언급했다시피 리턴값은 찾고자하는 값보다 큰 값의 첫번째 인덱스를 리턴하기 때문에, 고려해서 java로 작성해보자.
private static int upperBound(List<Integer> data, int target) {
int begin = 0;
int end = data.size();
while(begin < end) {
int mid = (begin + end) / 2;
if(data.get(mid) <= target) {
begin = mid + 1;
}
else {
end = mid;
}
}
return end;
}정리
기본적으로 이분탐색의 원리를 따르기때문에 시간복잡도는 O(logn)이고, 정확히는 O(long(리스트의 길이))다. 두 함수를 구축할때 팁은 어떤 값을 찾고자하는지 생각하면 된다.
그리고 return값을 upperbound에서 target보다 큰 인덱스값을 뽑아내는 이유는 아마,
upperBound() - lowerBound()를 통해서 중복값의 개수를 구하기 위해서이지 않을까 생각한다.
