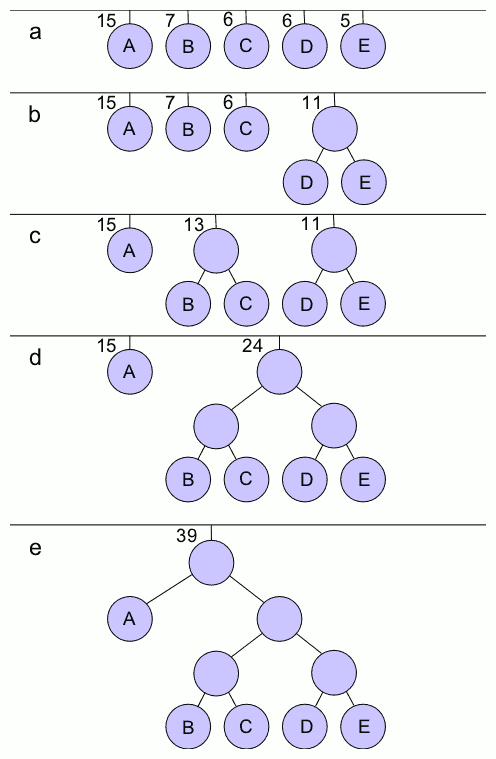
허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다. 허프만 코드(이진코드)는 Unix에서 파일압축에 사용되고, JPEG 이미지 파일 또는 MP3 음악 파일을 압축하기 위한 서브루틴으로도 활용된다.
허프만 코딩이란❓
처음에 허프만 코딩의 개념을 접한다면 한번에 이해하기 어려울 수 있다고 생각한다. 그래서 나는 설명하기에 좋은 비교방식을 이용해서 설명하려한다. 허프만 코딩은 앞에서 서론에서 언급했다시피 문자 빈도수를 이용해서 파일을 압축하는 과정이다. 그렇다면 기존에는 어떻게 사용하고있는데, 어떻게 얼마나 압축이 될까?
고정 길이 코드(fixed length code) vs 접두어 코드(prefix code)
고정 길이 코드는 대표적으로 아스키 코드가 있다. 아스키 코드는 항상 8bit의 길이를 가지고있다. 다루기에는 간단하지만, 저장 공간 활용에 있어서 제한이 있다. 이를 해결하기 위해서 가변 길이 코드(variable length code)가 존재한다.
가변 길이 코드 중에서도 접두어 코드는, 앞서 나온 문자가 다음에 나올 문자의 접두어가 되면 안되는 특징을 가진 코드다. 예를 들면 다음은 접두어 코드가 아닌 예다.
a : 01
b : 101
c : 010
위 코드에서 01은 010의 접두어이기 때문에 접두어 코드가 아니다. 반면 다음은 접두어 코드의 예다.
a : 01
b : 10
c : 111
이 접두어 코드를 아스키코드로 한다면? 총 24bit의 저장 공간을 소비한다. 반면에 압축한 상태 그대로 이진코드로 표현한다면 0110111로 7bit로 압축이 가능하게된다. 이처럼 입력 문자의 빈도수를 가지고 압축하는 것이 허프만 코딩이다.
원리
허프만 트리를 만들어서 압축을 하기위해서는 다음과 같은 원리도 수행된다.
- 압축할 파일을 스캔하여 각 문자의 빈도 수를 계산한다.
- 빈도 수를 우선순위로 최소힙 h를 구성한다.

- 빈도 수가 가장 작은 두 노드들을 삭제한다.
- 삭제한 두 노드 중에 작은 것을 왼쪽 자식노드, 큰 것을 오른쪽 자식노드로 하는 노드를 삽입
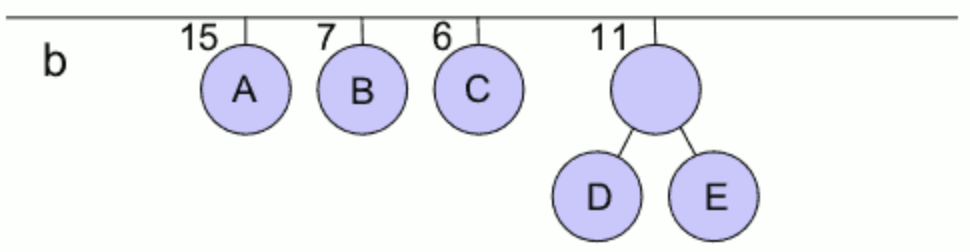
- 노드가 하나가 남을 때까지 반복한다.
- 마지막 노드가 루트 노드가 된다.
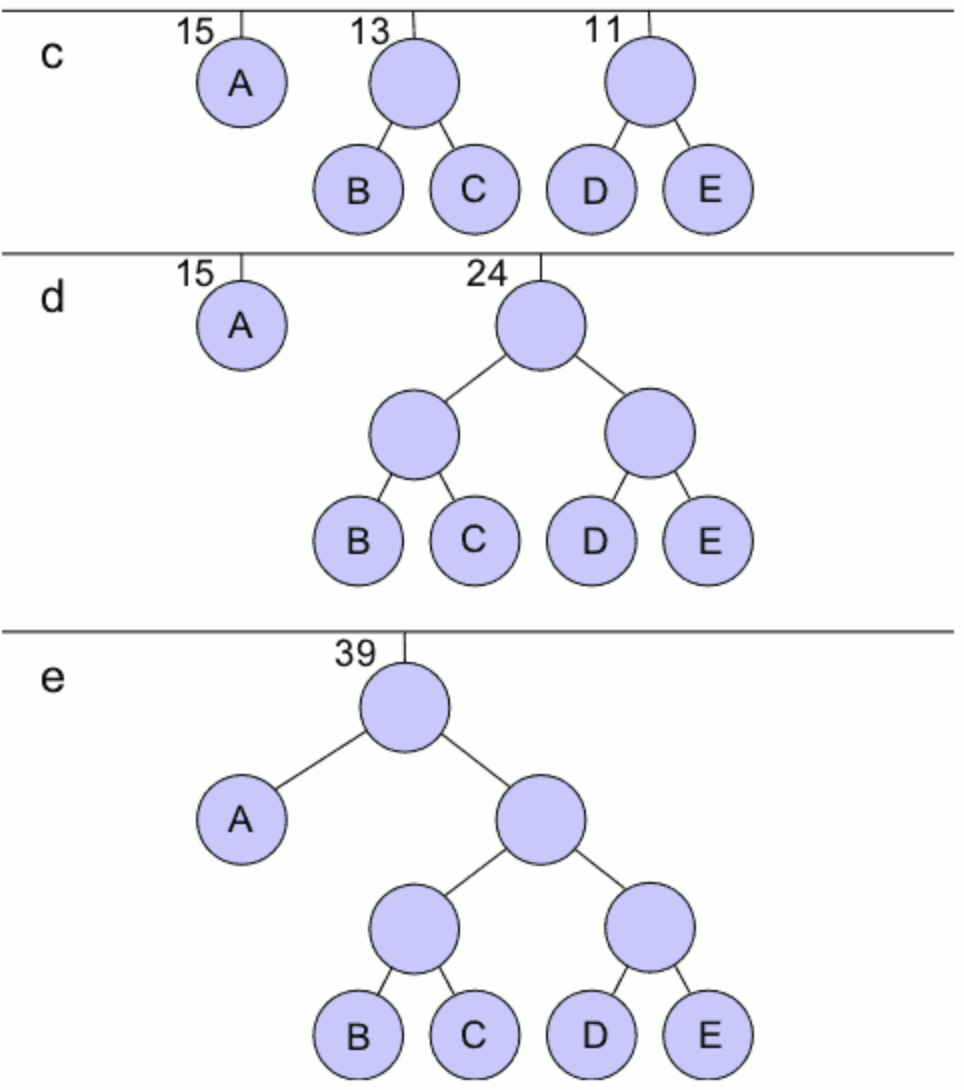
빈도 수가 높은 문자에는 짧은 이진코드(허프만 코드)를 부여하고, 빈도 수가 낮은 문자에는 긴 이진코드를 부여하여 압축 효율을 높인다.
구현
기본적으로 자료구조 Heap을 이용하기때문에, 기본적인 뼈대는 [자료구조] Heap을 참고하자. 다만, 위의 원리에서 언급한 6가지 순서에 대한 구현만 알아보자.
public class Entry {
private int frequency; // 빈도 수
private String word; // 노드의 문자 또는 내부노드의 합성된 문자열
private Entry left; // 왼쪽 자식
private Entry right; // 오른쪽 자식
private String code; // 허프만 코드
public Entry (int newFreq, String newVal, Entry l, Entry r, String newCode) {
frequency = newFreq;
word = newVal;
left = l;
right = r;
code = newCode;
}
public int getFrequency() {
return frequency;
}
public void setFrequency(int frequency) {
this.frequency = frequency;
}
public String getWord() {
return word;
}
public void setWord(String word) {
this.word = word;
}
public Entry getLeft() {
return left;
}
public void setLeft(Entry left) {
this.left = left;
}
public Entry getRight() {
return right;
}
public void setRight(Entry right) {
this.right = right;
}
public String getCode() {
return code;
}
public void setCode(String code) {
this.code = code;
}public class Huffman {
private Entry[] harray; // a[0]은 사용안함 (트리이기때문)
private int size; // 힙 사이즈
public Huffman(Entry[] heapArray, int initialSize) { // 생성자
harray = heapArray;
size = initialSize;
}
private boolean greater(int i, int j) {
return harray[i].getFrequency() > harray[j].getFrequency();
}
public Entry createTree() {
while(size() > 1) {
Entry e1 = deleteMin(); // 힙에서 최소 빈도수를 가진 노드 제거
Entry e2 = deleteMin(); // 힙에서 최소 빈도수를 가진 노드 제거
Entry temp = new Entry(e1.getFrequency() + e2.getFrequency(), // 빈도수 합
e1.getWord() + e2.getWord(), // 단어 이어붙이기
e1,e2," "); // e1,e2가 각각 새로운 노드의 오른쪽,왼쪽 자식노드로 붙기
insert(temp); // 새 노드를 힙에 삽입
}
return deleteMin(); // 1개 남은 노드(루트 노드)를 힙에서 제거하며 리턴
}
}복원(Decoding) 알고리즘
각 문자에 대응되는 허프만 코드는 prefix code이기 때문에 01#001#110과 같이 구분자를 사용하지 않고 01001110를 사용할 수 있다. 그렇다면 복원할때는 긴 비트 스트링을 어디서 끊어야할까?
기본적으로 알려진 방법으로는 첫번째 비트인 트리 상 루트노드로부터 비트가 0이면 왼쪽 1이면 오른쪽으로 타고 내려가다가 리프노드에 도달하는 순간에 리프노트가 가진 문자로 변환하고, 그 다음 비트들도 같은 방법으로 문자로 변환할 수 있다.
문자를 가지는 노드는 모두 리프노드다.
하지만 이 방법은 허프만 트리의 높이에 시간복잡도가 비례한다는 특성을 가지고 있다. 문자들의 빈도수에 따라서 적게는 O(logN) 부터 많게는 O(N)의 시간복잡도를 가진다. 따라서 최악의 경우 단 한개의 문자를 복원하는데 O(N)의 시간복잡도를 소요하는 상황이 발생할 수 있다.
