[Coursera] (1) NN and DL - W3

[W3] Shallow Neural Networks

1. 2-layer NN
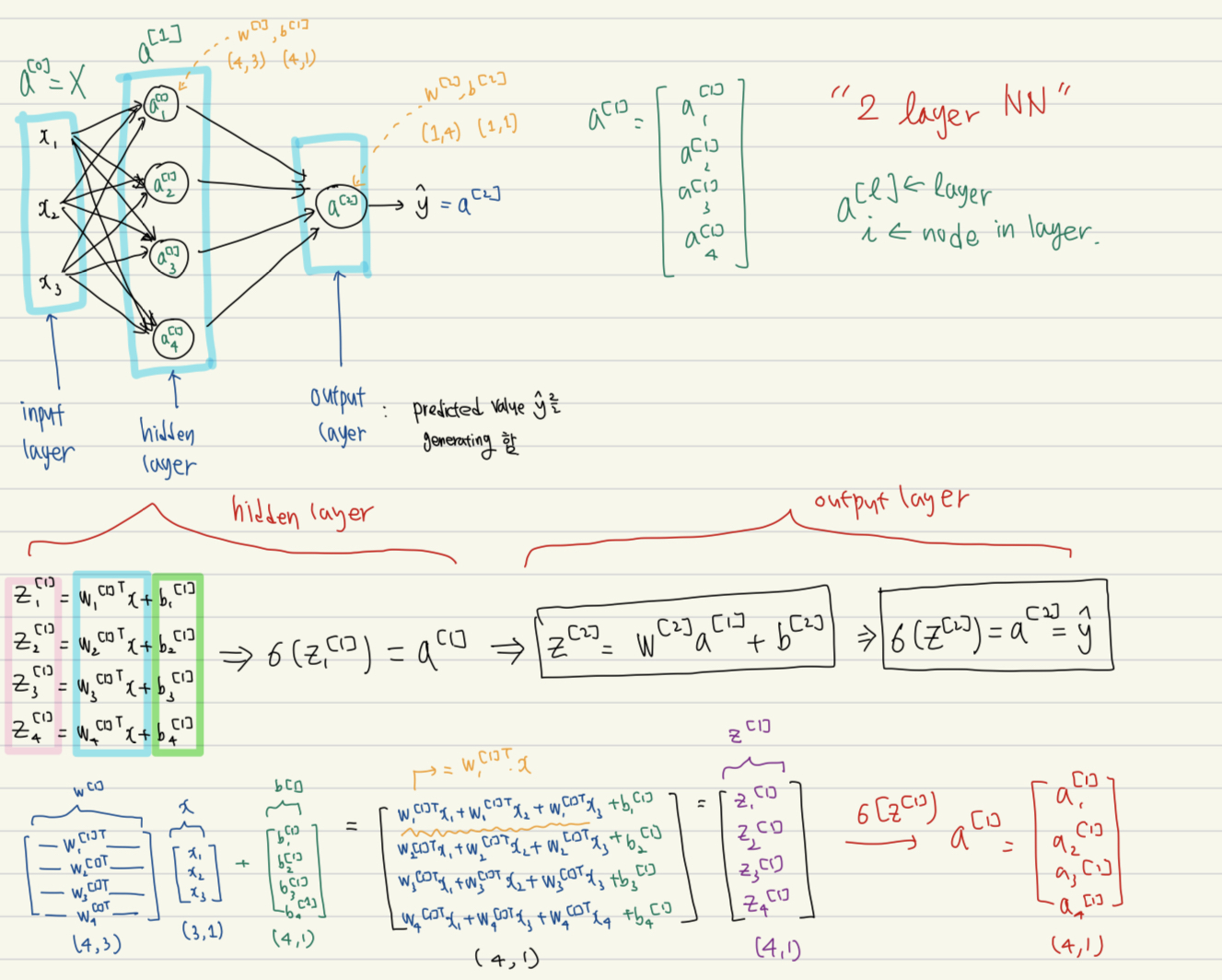
아래 그림과 같이 2-layer NN는 입력을 받는 input layer / hidden layer / predicted value ($\hat{y}$)를 generate하는 output layer 로 구성되어있다.
*cf) 보통 layer의 개수를 셀 때는 input layer는 count 하지 않는다고 한다.

• 하나의 hidden unit (원형 node) 에서는 아래의 계산이 이루어진다:
  (1) $z$ 계산 $(z = w^{T}x)$
  (2) $a$ 계산 $(a = \sigma(z))$
  
  

• 각 layer의 차원을 살펴보면 다음과 같다:
  (Hidden layer)
  - $w^{[1]}$는 4개의 hidden unit으로 이루어져있고 3차원 input ($x_1, x_2, x_3$)을 받으므로 (4, 3) 크기를 갖는다.
  - $z^{[1]}$는 (1)과 같이 계산되므로 (4, 1) 크기를 갖는다.
  - $a^{[1]}$는 $z^{[1]}$에 sigmoid를 취한 것이므로 똑같이 (4, 1) 크기를 갖는다.
  
  
  (Output layer)
  - $w^{[2]}$는 1개의 hidden unit으로 이루어져있고, 4차원 features ($a^{[1]}_1$, $a^{[1]}_2$, $a^{[1]}_3$, $a^{[1]}_4$)을 받으므로, (1, 4)의 크기를 갖는다.
  - $z^{[2]}$는 (1)과 같이 계산되므로, (1, 1) 크기를 갖는다.
  - $\hat{y} = a^{[2]}$는 $z^{[2]}$에 sigmoid --> 똑같이 (1, 1) 크기를 갖는다. 즉, $P(y=1|x)$ 확률이 나온다.
  
  

2. Vectorizing

• 우리는 이러한 계산을 single training example에 대해 벡터화하여 표현할 수 있다.
  

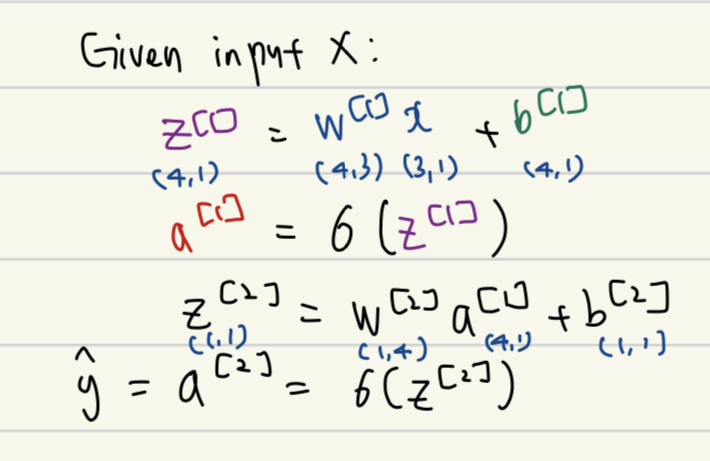
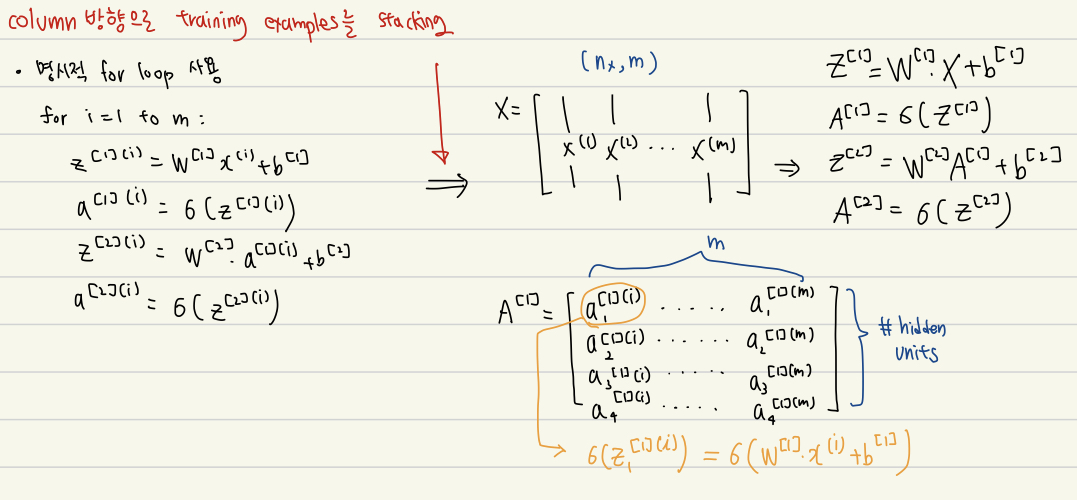
• 하지만, 우리의 training set에는 m개의 example이 존재한다. 전체 training set에 대해서 NN를 학습하려면 두 가지 방법이 존재한다.
  (1) 명시적으로 for loop 활용 --> 너무 많은 시간 낭비
  (2) Vectorization --> 두 행렬의 곱으로 수행 가능

• Vectorization: column 방향으로 training example을 stack하여 하나의 큰 행렬 ($X, W^{[1]}, Z^{[1]},...$)로 만든 다음 행렬 곱을 수행한다.
  
  
  

4. Activation Function
지금까지 우리는 activation function으로 sigmoid ($\sigma$)를 활용했다.
하지만 우리는 tanh나 ReLU 등 다른 activation function을 사용할 수 있다.

• 대표적인 activation function과 각각의 장단점을 아래에 정리했다.
  

• Activation function으로 nonl-inear function을 사용하는 이유:
  Activation function이 linear 함수이면, 선형 matrix에 선형 matrix를 곱해봤자 선형이기때문에 하나의 linear layer로 표현될 수 있다. 즉 layer를 깊게 쌓는 의미가 없어지게 된다.
  

• Activation function의 derivatives (도함수)
  

5. Gradient Descent for NN

• 우리가 학습해야할 parameters: $w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}$

• 입력 차원: $n^{[0]}$, #hidden unit: $n^{[1]}$, 출력 차원: $n^{[2]}$

• Computation graph
  

• Forward propagation
  $Z^{[1]}=W^{[1]}X + b^{[1]}$
  $A^{[1]} = g^{[1]}(Z^{[1]})$
  $Z^{[1]} = W^{[2]}A^{[1]} + b^{[2]}$
  $A^{[2]} = g^{[2]}(Z^{[2]}) = \sigma(Z^{[2]})$

• Back propagation
  

6. Random Initialization
만약 우리가 weight를 0으로 초기화 한다면?
서로 다른 hidden unit들이 항상 같은 값을 갖게 된다 --> hidden unit이 두 개 이상 있는 의미가 없어진다.
*cf) 이전에 배운 logistic regression의 경우 hidden unit이 어차피 한 개 이기 때문에 이때는 weight을 0으로 초기화해도 상관이 없었음

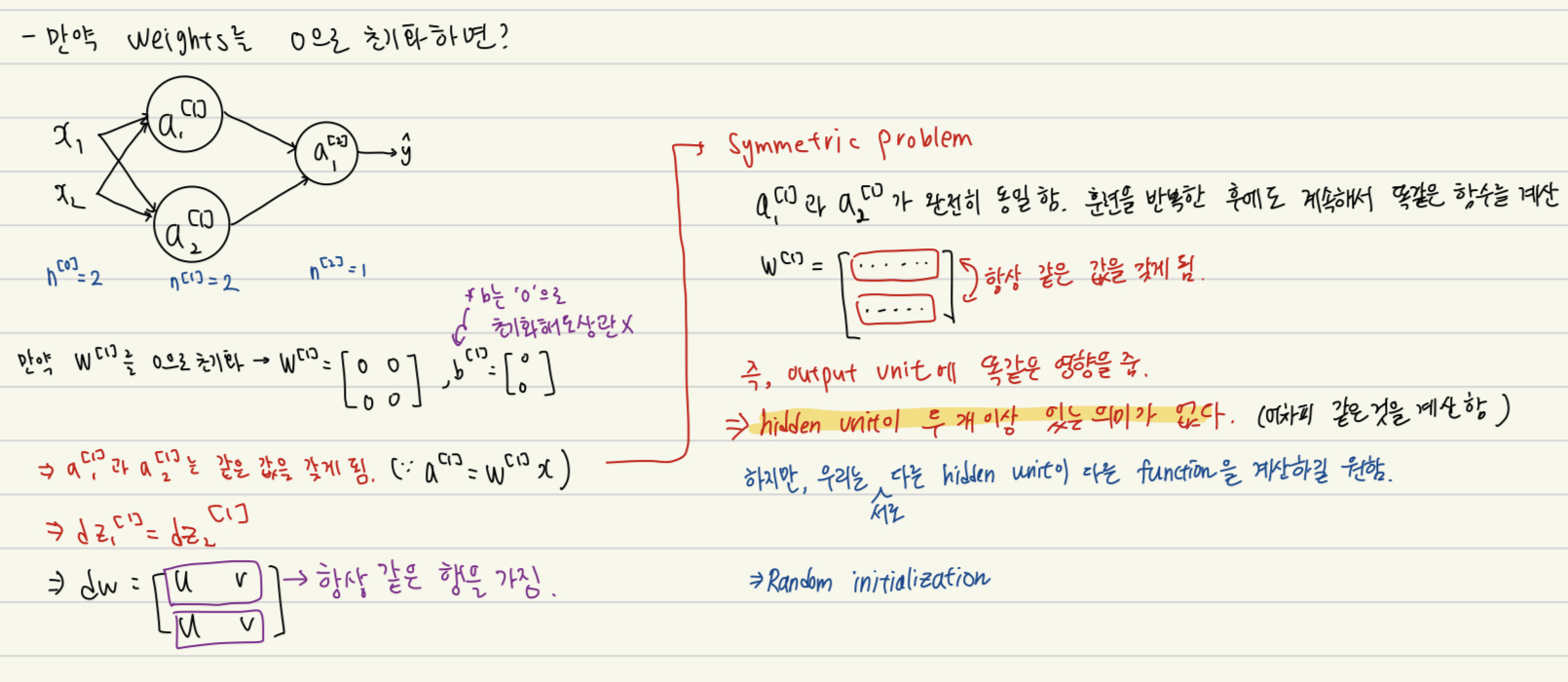
따라서 우리는 weight를 random하게 초기화해야한다.
이때, weight가 너무 커지지 않도록 0.01과 같은 작은 수를 곱해준다.