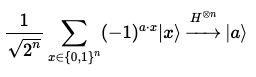The Bernstein-Vazirani Probelm
비트열 을 입력으로 받고, 0 혹은 1을 출력하는, 블랙박스(black-box, 내용을 알 수 없음) 함수 가 있다.
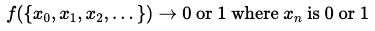
해당 함수는, 입력한 비트열을 특정 문자열 와 비트 곱 연산하여 반환한다.
즉, 입력 에 대해, (mod 2) 이다.
이 때, 를 찾는 것이 우리의 임무이다.
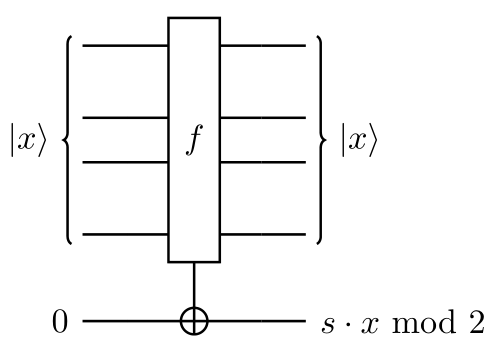
고전 가역 회로로써, Berstein-Vazirani 오라클은 아래와 같다.
The Classical Solution
고전 컴퓨터를 사용한 해결법은 다음과 같다.
오라클은 다음을 반환한다.
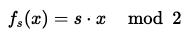
입력 에 대해, 미지의 비트열 는 가능한 입력들을 순차적으로 오라클에 쿼리함을 통해 밝혀낼 수 있다.

각각의 쿼리가 의 별개의 비트들(비트 )을 밝혀낸다.
예를 들어, 은 의 최하위 비트를 얻을 수 있으며, 은 의 최하위 다음 비트를 얻을 수 있다.
이는, 를 얻기 위해 함수 를 번 호출해야 함을 의미한다.
Bernstein-Vazirani Algorithm ( The Quantum Solution )
양자 컴퓨터를 사용하면, 입력 데이터들의 크기와 관계 없이, 함수 를 단 한번 호출하는 것 만으로 문제를 해결할 수 있다.
미지의 비트열을 찾기 위한 양자 솔루션인, Bernstein-Vazirani 알고리즘 순서는 다음과 같다.
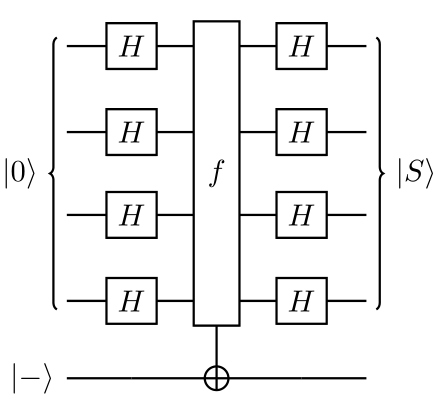
- 입력 큐비트들을 상태로 초기화한다.
출력 큐비트를 상태로 초기화한다. - 입력 레지스터에 하다마드 게이트를 적용한다.
- 오라클을 쿼리한다.
- 입력 레지스터에 하다마드 게이트를 적용한다.
- 측정한다.
양자 회로도는 아래와 같다.
-qubit 상태를 라 하자.
에 H-게이트를 적용하면 다음과 같이 변환된다.
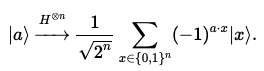
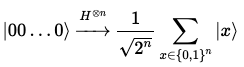
양자 레지스터 에 개의 하다마드 게이트를 적용하는 경우를 생각해 보자.
다음과 같은 양자 중첩 상태를 얻을 수 있다.
이 때, 이므로, 이다.
따라서, 위상 이 사라진다.
고전 오라클 는 mod 인 입력 에 대해 1을 반환하며, mod 인 입력 에 대해 0을 반환한다.
상태 인 큐비트에 의한 위상 반동을 사용하면 다음과 같이 변환할 수 있다.
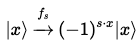
// input x에 대해서 s와 비트곱 연산한다.
// 이 때, 0과 1에 의해서(문자열의 비트와 input의 비트에 대해서) 1이 나왔으면 phase kickback에 의해 controll qubit의 phase가 |+>에서 |->로 뒤집힘
해당 알고리즘은 에 하다마드 변환을 적용하여 얻은 양자 중첩 상태를 양자 오라클 에 쿼리하는것 만으로 미지의 비트열을 찾아낸다.
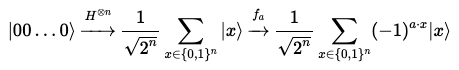
하다마드 게이트의 역은 하다마드 게이트 그대로이므로, 우리는 다음과 같이 를 구할 수 있다.