문제

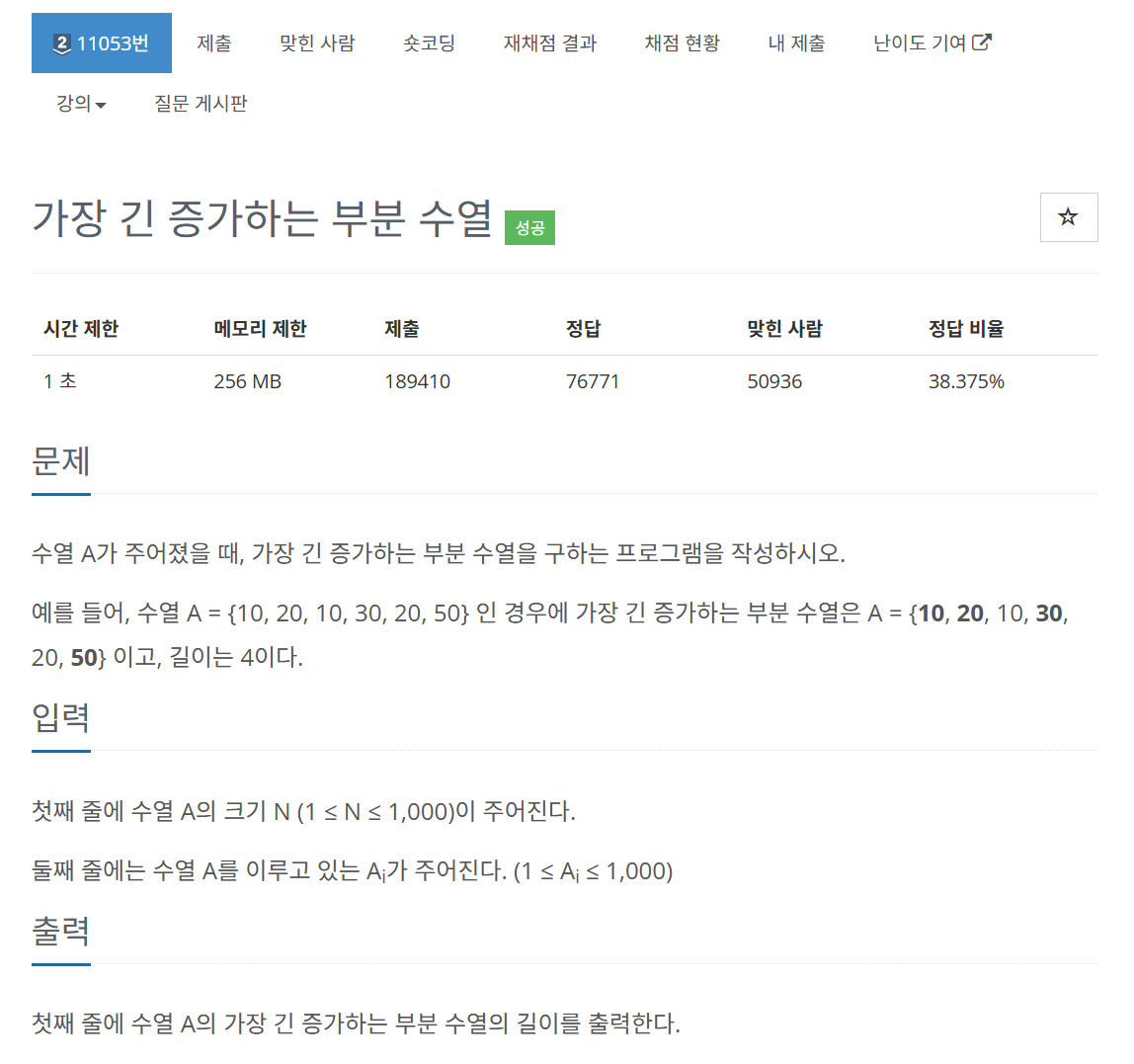
문제 이해

DP에서 LIS라는 부분수열을 구하는 문제라고 한다. 코드가 정말 짧지만 강력하다. 이 문제의 다른 사람의 풀이를 보고 이해하는데 시간이 꽤 걸렸다. 약간 DFS/BFS를 처음 접할때와 매우 비슷했다. 이해가 너무 안되어서 코드 한줄한줄에 따라 dp값이 어떻게 처리되는 지 한참을 반복했다.

이해가 안 갔던 부분은 만약 수열이 [10 20 15 21 25 30]일때, 10을 체크하고 20을 체크했고, 21을 체크할때 10-15-21의 부분 수열을 어떻게 구분해낼지가 이해가 안되었다. 왜냐면 조건문의 코드가 arr[i] > arr[j]라서, 21보다 작은 값일때 모두 조건문을 통과하기 때문이다. 더 헷갈렸던건 내가 남긴 코드와는 다르게 좀 더 복잡해서 그런 것 같다.

[10 20 15 21 25 30] 의 수열로 설명을 한다면

먼저 알아야 할것은 이전의 인덱스 값이 현재 인덱스 값보다 작으면 현재 dp의 값과 이전 dp값에 1을 더해서 둘 중에 큰 값을 dp에 넣는다. -> 결국 이 로직 덕분에 값이 잘들어간다. 자세한 건 아래에서 설명한다.

기준 값의 인덱스 i
진행하는 현재 값의 인덱스 j

if arr[i] > arr[j]: # i번째보다 그전 값이 작을때마다
            dp[i] = max(dp[i], dp[j]+1)

수열
[10 20 15 17 21 25 30]

dp
[1 1 1 1 1 1 1]
dp 초기값이 1인 이유: 어차피 자신을 포함하면 일단 1이기 때문

i = 0일때
10일때는 dp[0] = 1 (첫 값이라서 비교할 값이 없음)

dp = [1 1 1 1 1 1 1]

i = 1일때
20일때는 10이 20보다 작기 때문에 dp[1], dp[0]+1을 비교, dp[0]+1= 2이므로 2를 대입. -> 이런 경우에는 [10 20] 라는 부분수열이 성립된 것이다.

dp = [1 2 1 1 1 1 1]

i = 2일때
15일때는 10이 작은 숫자이기 때문에 dp[0]+1 dp[2]를 비교해서 2가 대입됨 -> [10 15] 부분수열이 성립된 것이다.

dp = [1 2 2 1 1 1 1]

i = 3일때
17이기에 10, 15에서 걸린다. 10일때는 [10 17]이 성립되어서 dp[i] = 2, 15도 17보다 작기 때문에 dp[2]+1, dp[3]을 비교해서 dp[1]+1 = 3 라서 dp[i] = 3이다. 이 경우는 [10 15 17] 부분 수열이 성립된 것임.

dp = [1 2 2 3 1 1 1]

i = 4일때
21일때는 10, 20, 15, 17에서 걸린다. 10일때는 dp[0]+1, dp[4] 여서 dp[i] = 2가 된다. 20일때는 dp[1]+1, dp[i]를 비교해서 dp[1] +1 = 3이라서 dp[i]가 3이 된다.

dp = [1 2 2 3 3 1 1]

여기서 중요한게 21을 기준으로 가장 긴 부분수열은 [10 15 17 21]이지 [10 20 21]이 아니다. 20에서 한번 걸려서 dp값이 바뀌는데 이걸 어떻게 거르는지 이해가 안되었다. 계속 진행을 하면 알게 된다.

15일때 걸리면 dp[2]+1 = 3, dp[i] = 3이라서 3으로 유지
17일때 걸리면 dp[3]+1 = 4, dp[i] = 3이라서 4로 대입
이렇게 걸러진다.

dp = [1 2 2 3 4 1 1]

이런 방식으로 가장 긴 부분수열을 찾을 수 있다. 계속 진행하면 나머지 dp도 수정된다. 그러면 dp에서 가장 큰 값이 가장 긴 부분수열이 된다.

이해하기 어려웠지만 재밌다. 약간 매운데 맛있게 매운 느낌같다.

코드

# 백준 11053번 가장 긴 증가하는 부분 수열

N = int(input())
arr = list(map(int, input().split()))

#dp리스트 초기값은 모두 1이다. 어떤 값에서 시작하든 일단 자신을 포함해서 1이기 때문에
dp = [1] * N

for i in range(1,N): # 1부터 시작하는 이유: 0부터 시작하면 안에 있는 반복문이 어차피 안돌아감
    for j in range(i): # i를 끝값으로 줘서 i전에 있는 값만 탐색한다
        
        if arr[i] > arr[j]: # i번째보다 그전 값이 작을때마다
            dp[i] = max(dp[i], dp[j]+1) # 이어져온 부분집합에 1을 더한게 현재dp값이니까 두개를 비교 해서 대입입

print(max(dp))