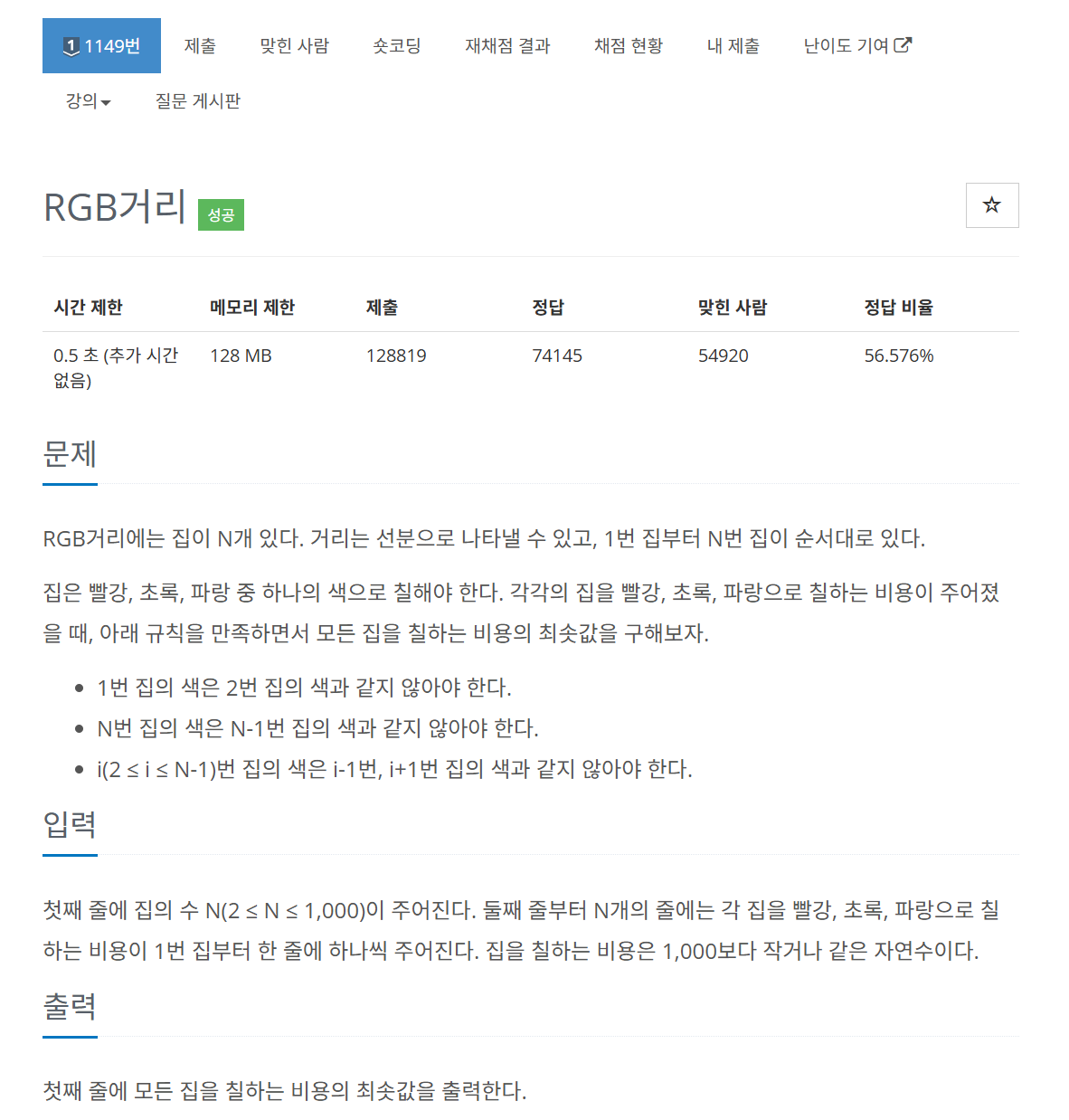
문제

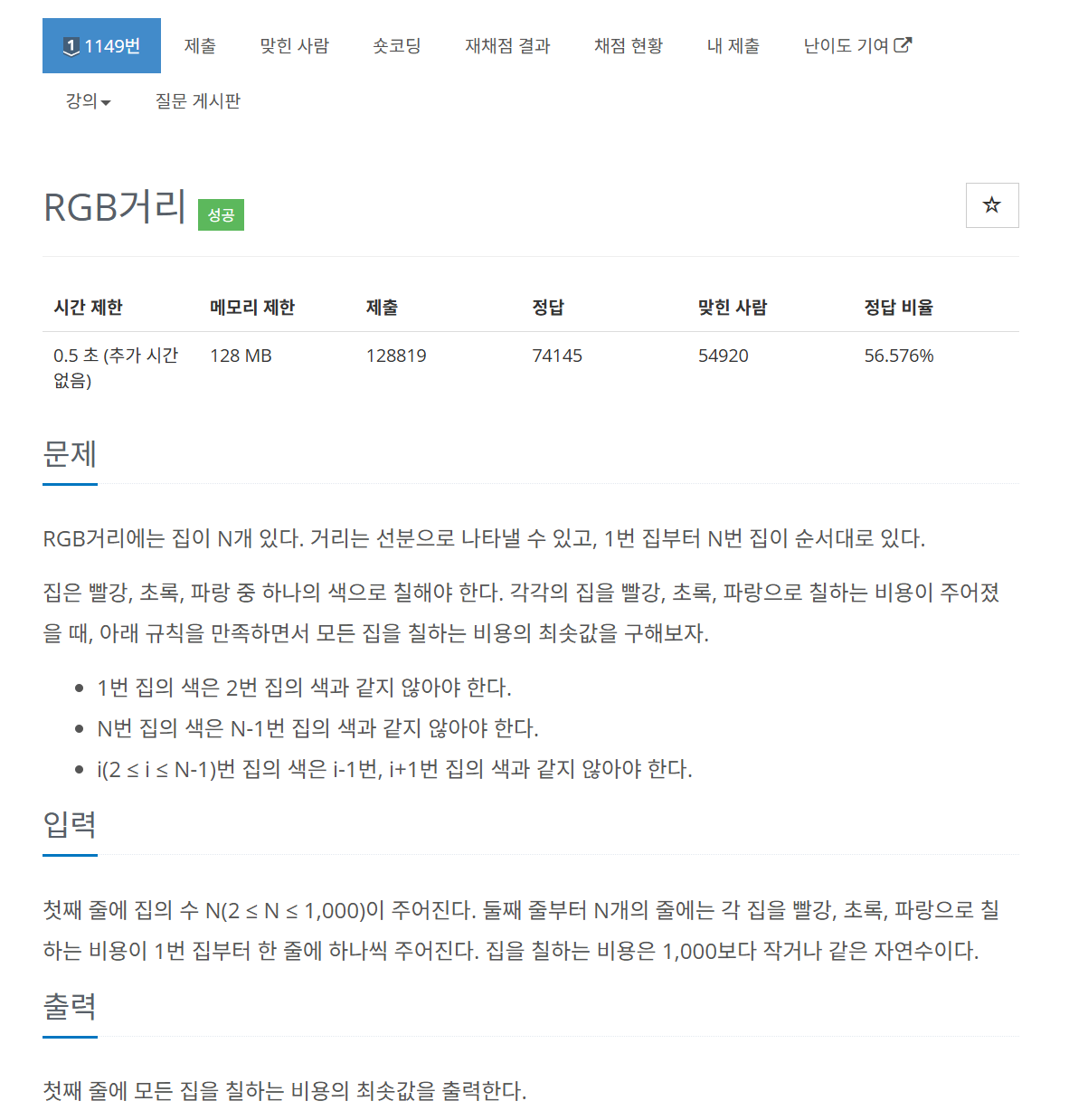
문제 이해

이런 유형이 조약돌 문제라고 하는 DP대표 문제라고 한다. 너무 재밌다. DFS/BFS를 처음 배울때도 재밌었는데, DP도 그만큼 재밌는 것 같다. 생각하고 문제를 풀이하는 게 체계적이라서 그런 것 같다.

아무튼 3가지 중에서 하나씩 골라가면서 N개의 뽑았을때의 최솟값을 구해야한다. 여기서 문제가 두개가 연속으로 선택되면 안된다. i번에서 1번을 택했으면, i+1번에서는 1번을 제외하고 선택해야한다. 이것 때문에 문제가 어려워진다. 애초에 모든 경우를 다해보는 것도 힘들어지고, 가장 작은 값만 골라서 간다고 해도 그게 최솟값일 가능성은 매우 낮다.

그래서 이 문제는 DP로 풀어야한다. 하지만 DP로도 한 경로를 특정해서 찾기는 어렵다. 여기서 꺾어서 생각해야하는 것, 떠올려야할 발상은 모든 경우의 최솟값을 구하는 것이다.

색깔대신 순서로 나타내면

이렇게 집과 비용을 입력받으면 똑같은 리스트 크기로 DP를 만든다.(왼쪽은 입력받은 행렬, 오른쪽은 DP)

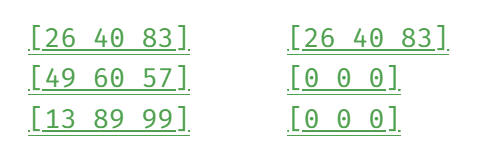
DP리스트의 첫번째 인덱스의 값은 입력받은 리스트와 같도록 초기값을 설정한다.
그리고 각각의 경우의 최솟값을 넣어준다.

즉, DP[1][0]은 DP[0][1], DP[0][2]에서 더 작은 값에 Matrix[1][0]을 더한 값이 최솟값이다. 같은 방식으로 DP[1][1]은 DP[0][0], DP[0][2]에서 더 작은 값에 Matrix[1][1]을 더한 값이 최솟값이다. 이를 계산하면 DP는 아래와 같다.

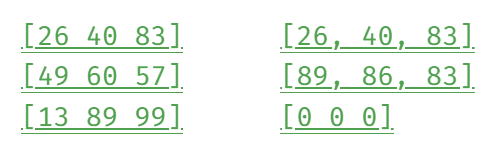
마지막 집까지 경로를 계산하면 아래와 같다.

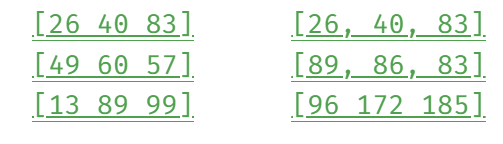
DP의 마지막 값중에서 가장 작은값은 처음부터 끝까지 다른 색으로 집을 칠하면서 얻을 수 있는 값의 집합이다. 셋 중에 가장 작은 것이 최솟값이다.

코드

# 백준 1149번 RGB거리

N = int(input())

# dp역할을 하는 min_cost리스트

cost = [[0, 0, 0]] # 인덱스 맵핑을 위해서 0번 인덱스 추가
for _ in range(N):
    cost.append(list(map(int, input().split())))

dp = [[0, 0, 0] for _ in range(N+1)]

# dp 1번인덱스 초기화
dp[1][0] = cost[1][0]
dp[1][1] = cost[1][1]
dp[1][2] = cost[1][2]

# 각 인덱스별 최소 비용 구하기
# 모든 경우를 모두 구해줄거다. 3가지 중에 어디로 갈지를 모르니 모두 구하고 결과값만 비교할 거임임
for i in range(2, N+1):
    # dp[i][0], dp[i-1][0] 같은 자리 이전 제외외
    dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + cost[i][0]

    # dp[i][1]
    dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + cost[i][1]

    # dp[i][2]
    dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + cost[i][2]

print(min(dp[N]))