OS - 1.6 (PV) (5) Process Context Switch

  지난 시간 소개한 개념은 Limited Direct Execution으로, CPU Virtualization 시 Performance 문제로 인해 Direct Execution을 도입했지만, 그로 인해 발생하는 Restricted Operations Accessing 문제와 CPU Control 회수 방법 문제가 나타나고, 이들에 대한 해결책으로 Dual Mode Operations를 말미암은 Limited Direct Execution 이론이 개발되었다고 설명했다.

Limited Direct Execution : CPU Virtualization 시 나타나는 성능 문제를 해결하기 위해 Direct Execution을 도입하되, 그로 인해 파생되는 Restricted Operations Accessing & CPU Control Retrieving 문제를 방지하고자 User Program에 Limit을 가한다는 것!

  그래서 우린 지난 시간 Dual Mode Operations로 인해 만들어진 System Call 개념을 열심히 공부했다. 이는 곧 Trap으로, Trap을 다시 한 번 간단히 설명하자면 다음과 같다.

• Trap의 이유

  • System Call
  • Disk I/O
  • Keyboard Interrupt 등

• Trap Handler : 각각의 Trap Interrupt Number에 따른 Handling Routine을 수행하는 Code

  • Trap Table, IDT, 또는 Interrupt Vector Table이 있다.
    • 각각의 Trap에 대한 Handler들의 주소를 가지고 있다.
    • OS는 HW에게 각 Trap Handler의 Address를 알려준다.
    • 이때 사용되는 Instruction(Interrupt/Trap Instruction)도 Privileged Instruction이며, 따라서 User Mode에선 사용할 수 없다. ★

  이렇게 Trap에 대한 개념은 마무리하자.

Cooperative Approach

  이제 Direct Execution의 두 번째 문제 'Switching between Processes(How to get back the CPU Control from a running process)'에 대한 해결책을 알아보자.

• Direct Execution 시, 여러 Process가 동시에 돌아가는듯한 Process Virtualization이 실현되기 위해선 Process Context Switch가 일어나야 한다.
  • 이때, OS가 Process 간의 Switch가 일어나게 하기 위해선 Running Process로부터 CPU Control을 얻을 수 있어야 한다. ★★★
    • "어떻게 CPU Control을 가져올 것인가?"
      • 여기엔 두 가지 방법론이 등장한다. 그 중 첫 번째는 이 Cooperative Approach이다.

Cooperative(Non-Preemptive) Approach : Program이 돌다가 스스로 CPU Control을 놓도록 만들어주자. 더 이상 CPU를 사용할 필요가 없다면, 알아서 포기(Yield)하게 하자!

Preemptive : '선점하는'이란 뜻

Non-Preemptive = Cooperative : OS가 CPU Control을 선점하지 않고, Process가 알아서 놓도록 만들어준다는 의미 ★★

• Process가 주기적으로 CPU Control을 알아서 놓도록 만들어주자는 것이다.

  • 'yield' 기능의 System Call 같은 것을 두어서!

  • OS가 어떤 Task, Job을 돌릴지는 결정할 수 있다. (Schedule은 OS가 함) ★

  • User Application Program이 CPU를 점유한채 돌다가, 무언가 잘못된 일을 할 경우 스스로 CPU를 놓을 수 있도록 설계해야한다. ★

    • ex) Division by Zero, Kernel/Device Memory Access 등

• 초창기의 운영체제들이 이러한 방식을 채택한 바 있다.
  • Apple의 초기 Macintosh OS가 이러했다.

허나, 이 방식엔 중대한 문제점이 존재했다. (그래서 구식인 것)

"만약, Process가 모종의 이유로 중간에 yield하지 않으면 어쩔 것인가? 의도적으로 무한루프를 돌면서 yield를 하지 않으면 어쩔 것인가?"

Process can be stuck in a infinite loop. We can only reboot the system if in this case....

  그래서 등장한 것이 아래의 Preemptive(Non-Cooperative) Approach이다.

Preemptive Approach

  'Preemptive', 'Non-Cooperative', 즉, OS가 Process와 협력하지 않고 자신이 스스로 CPU Control을 선점하는 방식이다.

Non-Cooperative(Preemptive) Approach : OS가 CPU Control을 직접 가져오는 방식

무엇을 통해서? 'Timer-Interrupt'를 통해서!

• Computer System의 Booting과 동시에 OS는 Timer Hardware를 실행시킨다.

  • Timer Hardware는 잠깐의 밀리초를 주기로 해서 Interrupt를 발생시킨다. ★

  • Timer Interrupt가 발생하면,

    • Running Process가 Suspend된다.
    • 그 Process의 State, 즉, Context를 Save한다. ★
    • 미리 정의된 OS의 Interrupt Handler가 수행된다. ★
      • OS 내부에 Timer Interrupt Handler가 있고, 이 Handler는 OS가 CPU Control을 가져오도록 하는 기능이 있다. ★★★

• 이러한 Preemptive Approach는 상기한 Cooperative Approach에서 발생할 수 있는 Infinite Loop 문제에서 자유롭다.

Context Switch

Context of a Process : PC(Program Counter), CPU Registers Set Values, Process State, Memory 관리 정보 등의 Process와 관련된 정보들

• CPU가 현재 Running Process에서 다른 Process로 Switch할 때, System은 반드시 Old Process의 Context(State)를 Kernel Stack 또는 PCB에 저장해야 한다. ★★★

  • 나중에 Old Process의 Turn이 다시 돌아오면 그대로 Resume하기 위해!

• 또한, New Process의 Kernel Stack/PCB로부터 New Process의 Context를 가져와 Restore해야한다.

  • 지금 바로 New Process를 Resume하기 위해!

이러한 일련의 전환 과정이 바로 Process Context Switch이다. ★

• Context Switch Time은 Pure Overhead이다.
  • Switch하는 동안 CPU는 정말 말그대로 아무런 '유의미한' 일을 하지 않기 때문이다.
    • 이 Overhead는 Machine에 따라 달라진다.

Context Switch는 Pure Overhead이기 때문에, 이 시간을 줄여야 System의 수행 속도가 좋아진다.

따라서, Context Switch와 관련한 Code는 Assembly로 Compact하게 작성해야한다. ★★

현대 OS에선 이러한 Code가 이미 최대로 효율적이기 때문에, 이 Overhead를 더 줄이기 위해선 HW적인 도움이 필요해진다.

• 이러한 Context Switch Overhead는 수 마이크로초 정도 소요된다.
  • HW의 도움에 따라 달라진다. ★
    • 여러 개의 Registers Set을 두고, Pointer만을 넘기는 식으로 변형할 수 있겠다.
    • 또는, Registers Set의 Load/Store 과정을 좀 더 빠르게 수행하는 HW Instructon을 마련할 수도 있겠다.

  아래는 xv6에서의 Context Switch Code이다.

.globl swtch
swtch:
	# Save Old Process's Context
	movl 4(%esp), %eax 		# Old Pointer를 eax Register로!
	popl 0(%eax) 			# Old Instruction Pointer
	movl %esp, 4(%eax) 		# Old Stack Pointer
 	movl %ebx, 8(%eax) 		# Registers Set Values
 	movl %ecx, 12(%eax)
 	movl %edx, 16(%eax)
 	movl %esi, 20(%eax)
 	movl %edi, 24(%eax)
 	movl %ebp, 28(%eax)

 	# Load New Process's Context
 	movl 4(%esp), %eax 		# New Pointer를 eax Register로!
 	movl 28(%eax), %ebp 	# Registers Set Values를 복구
 	movl 24(%eax), %edi
 	movl 20(%eax), %esi
 	movl 16(%eax), %edx
 	movl 12(%eax), %ecx
 	movl 8(%eax), %ebx
 	movl 4(%eax), %esp 		# New Stack Pointer
 	pushl 0(%eax) 			# New Instruction Pointer (Resume 지점)
 	ret	 					# Restore 완료!

Interrupt Handling Protection

  잠시 개념 설명을 멈추어, 다음과 같은 의문사항에 대한 답변을 하고 가겠다.

만약, System Call로 인한 Trap Handling이나, 또는 바로 위의 Context Switch로 인한 Timer Interrupt Handling과 같은 Interrupt Handling 시에, 그 과정에서 중간에 다른 Interrupt가 발생하면 어떡하나요?

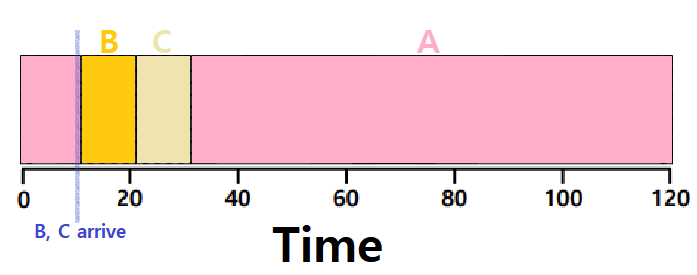
OS에서 Interrupt Handling 시에, 그 Handling 앞 뒤로 'Interrupt Disabling & Enabling' Routine이 존재한다.

Handling에 앞서, 다른 Interrupt를 잠시 Disabling하고, Handling이 끝나면 다시 Enabling하는 것이다. ★★★

  그래서 지난 포스팅에서 다음의 그림에 'Disabling, Enabling'이 있던 것이다. ★

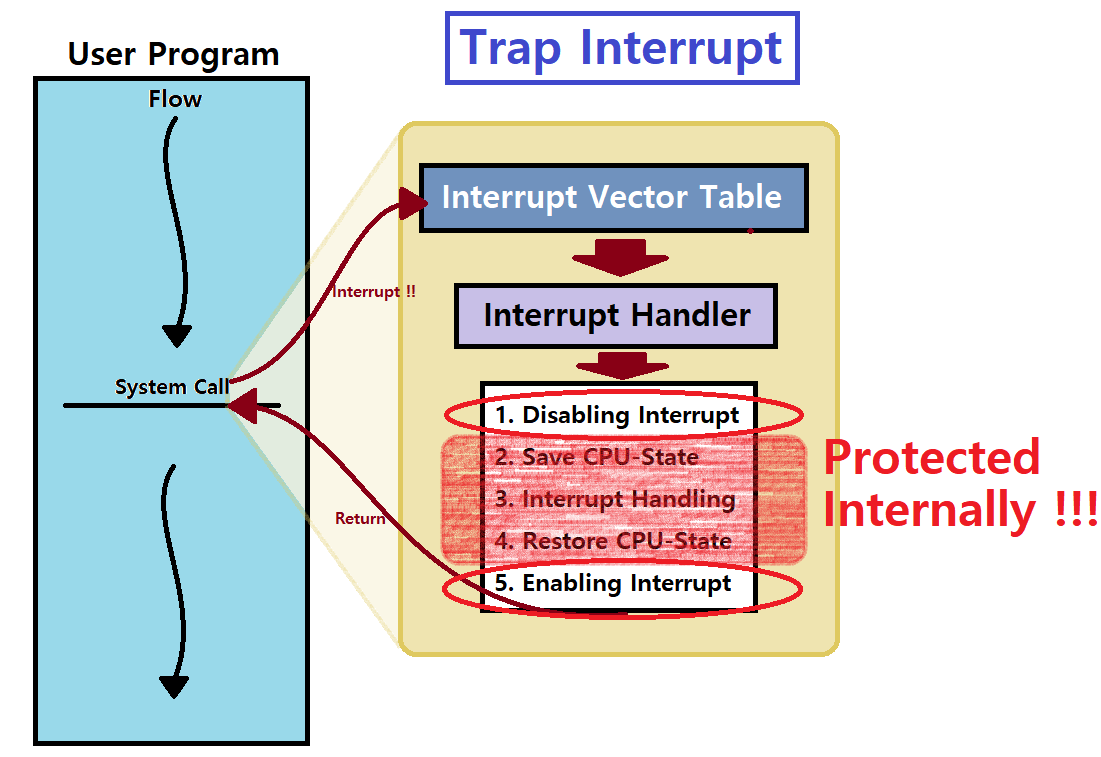
• Semaphore와 같은 동기화 기법을 통해 이를 구현한다.

• 추후 더 설명하도록 하겠다.

Scheduling Algorithms

  Limited Direct Execution의 일환인 Context Switch를 이제 제대로 이해했을 것이다. 이러한 Process Context Switch에선 다음의 Issue가 존재한다.

"Context Switch 간에 새로운 Process를 어떠한 Policy(Algorithm)에 의거해 골라올 것인가?"

  이러한 Issue는 곧 'Scheduling' 문제가 된다. 우리는 지금부터 OS의 Scheduling Algorithm대해 알아볼 것이다. 학습에 앞서 다음과 같은 가정을 깔고 가자. 학습의 편의성을 위해서 가정하는 것이다.

1) 각각의 Process는 동일한 시간동안 수행된다.
2) 각각의 Process의 수행 시간은 미리 알 수 있다.
3) 모든 Process는 같은 시간에 도달한다.
4) 모든 Process는 CPU만 사용한다. (I/O가 없음)

  그리고, 다음의 Performance Metric을 채택하여 평가할 것이다.

Turnaround Time : 'Process가 수행을 마친 시각' - 'Process가 System에 도착한 시각'

T_turnaround = T_completion - T_arrival

즉, Process가 Ready Queue에 들어왔다가 나가는데까지 걸리는 시간이다. ★

Waiting Time : Process가 Ready Queue 안에서 '기다리는' 총 시간 ★★★

T_waiting = T_turnaround - T_running

  이 밖에 Response Time도 확인해볼 것이다. (추후 설명)

  또한, Fairness Metric도 볼 것이다.

Fairness : 모든 Process가 공평하게 CPU를 점유하는지 ★★★

Performance와 Fairness는 Trade-Off 관계에 있다. ★★★

FIFO Algorithm

  가장 Naive한 Scheduling Algorithm으로, 말그대로 FIFO(First-In, First-Out)의 논리대로 움직인다. 'FCFS(First-Come, First-Served)'라고도 한다.

• 매우 간단하고 구현이 쉽다.

  아래의 예시를 보자.

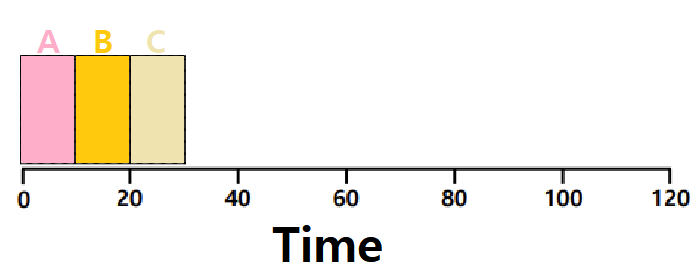
• ProcessA, ProcessB, ProcessC가 동시에 System에 Arrive했다. 미세하게 ABC 순서로 들어갔다고 해보자. FIFO Algorithm이다.

  • A는 0초에서부터 10초간, B는 0초에서부터 20초간, C는 0초에서부터 30초간 Ready Queue 안에 존재한다.

    • 따라서 Turnaround Time은 아래와 같이 계산할 수 있다.
      • 𝑨𝒗𝒆𝒓𝒂𝒈𝒆 𝒕𝒖𝒓𝒏𝒂𝒓𝒐𝒖𝒏𝒅 𝒕𝒊𝒎𝒆 = (𝟏𝟎 + 𝟐𝟎 + 𝟑𝟎) / 𝟑 = 𝟐𝟎     (초단위)

  • Average Waiting Time의 경우, 수행 시간 10초씩을 각각의 T_turnaround에서 빼주어 계산할 수 있겠고, 따라서 10초가 나오겠다.

Convoy Effect

  이러한 FIFO Algorithm은 딱봐도 문제가 있을 것처럼 보인다. 우리가 깔았던 가정 중에, '모든 Process의 수행 시간이 같다'는 가정만 없애도 바로 나타난다.

"만약, FIFO Algorithm 하에서, 먼저 도착한 Process의 수행 시간이 비약적으로 길면 어떻게 할 것인가?"

  아래 그림을 보자. 만약, Ready Queue에서 앞 쪽 Process의 수행 시간이 상대적으로 오래 걸릴 경우 그 뒤의 모든 Process들의 T_turnaround는 길어질 것이다. Process들이 과도하게 기다려야 한다. 즉, 비효율적이다.

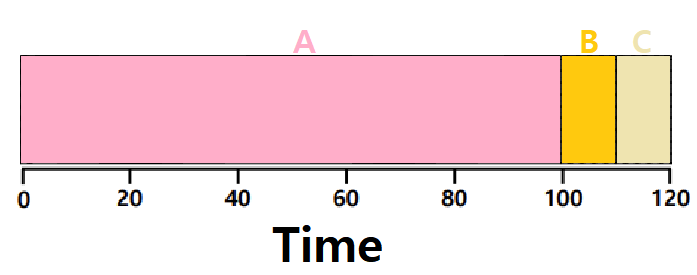
𝑨𝒗𝒆𝒓𝒂𝒈𝒆 𝒕𝒖𝒓𝒏𝒂𝒓𝒐𝒖𝒏𝒅 𝒕𝒊𝒎𝒆 = (𝟏𝟎𝟎 + 𝟏𝟏𝟎 + 𝟏𝟐𝟎) / 𝟑 = 𝟏𝟏𝟎     (초단위)

  반면, 위 그림에서 BCA 순서로 들어온다고 생각해보면, 평균 Turnaround Time이 (10 + 20 + 120)으로 50초가 될 것이다. 즉, Arrival 순서와 Process의 수행 시간에 따라 Performance가 상당히 오르락 내리락하는, 불안정한 모습을 보이는 것이다.

여담) convoy : '화물, 수송대'의 의미

• Process의 구분 (하는 일 기준)

  • CPU Bound Process : CPU Burst Time이 긴, Intensive한 Job

    • 위 예시 그림의 ProcessA와 같이!

  • I/O Bound Process : CPU Burst Time이 짧은, 즉, CPU는 적게 쓰고 I/O를 많이하는 그러한 Job

    • 위 예시 그림의 ProcessB/C와 같이!

  한 가지 예시 상황을 들어보자.

• Ready Queue에 여러 Process가 있고, 그 중 I/O Bound Process가 먼저 CPU를 점유했다고 하자. 짧게 CPU를 소모한 다음 I/O Operation을 위해 I/O Queue로 이동할 것이다. ★

• 그 다음은 CPU Bound Process가 스케쥴되었다. CPU Burst Time이 크기 때문에 오랜 시간 CPU를 잡아먹는다.

  • 이때, 앞 전의 I/O Bound Process가 I/O Operation을 마치고 다시 Ready Queue로 돌아왔다.
    • 허나, CPU Bound Process는 여전히 CPU를 잡아먹고 있다. 여러 I/O Bound Process가 이 뒤에서 기다리기만 해야한다.
      • I/O Device가 할 일이 없게 된다. Idle(게으른) I/O Device가 되는 것이다. ★★

• CPU Bound Process가 수행을 드디어 마쳤다. 이 Process는 이번에 I/O를 하려고 한다. 따라서 I/O Queue로 들어간다.

  • 와중에 I/O Bound Process들이 CPU를 짧게 짧게 소모한 다음 다시 I/O를 하러 I/O Queue로 속속들이 모이고 있다.
    • 허나, CPU Bound Process는 여전히 I/O를 사용한다고 해보자. 그러면 이번엔 CPU가 Idle하게 될 것이다.

이처럼, CPU Bound Process에 의해 I/O Bound Process들이 Ready Queue 혹은 I/O Queue에서 기다리기만 하게 되는 효과를 Convoy Effect라 한다. ★

FIFO Algorithm은 이러한 Convoy Effect를 가지고 있기 때문에 Turnaround/Waiting Time이 언제든지 커질 수 있는 위험이 존재한다. ★★

~> 그래서 등장하는 개념이 바로 아래의 SJF Algorithm이다.

SJF Algorithm

  FIFO Algorithm의 단점을 해결하기 위해 나온 방식이 'SJF(Shortest Job First) Scheduling Algorithm'이다. 이름 그대로, 수행 시간이 짧은 Process부터 먼저 돌리겠다는 것이다.

• 가장 수행 시간이 짧은 Job부터 돌리고, 이어서 그 다음으로 짧은 Job을 돌리고,...
  • FIFO처럼 Non-Preemptive하다. 즉, Process 수행이 다 끝이나야 다음 Process가 돌아간다. ★★★

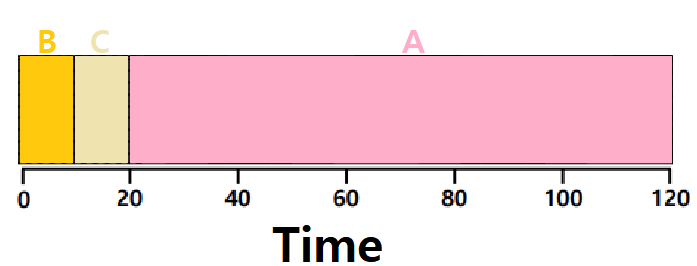
• ABC가 동시에 Arrive했다고 하면, B, C, A 또는 C, B, A 순서로 Schedule하는 것이다.

𝑨𝒗𝒆𝒓𝒂𝒈𝒆 𝒕𝒖𝒓𝒏𝒂𝒓𝒐𝒖𝒏𝒅 𝒕𝒊𝒎𝒆 = (𝟏𝟎 + 𝟐𝟎 + 𝟏𝟐𝟎) / 𝟑 = 𝟓𝟎     (초단위)

~> 앞선 FIFO에 비해서 훨씬 더 효율적으로 변화했다.

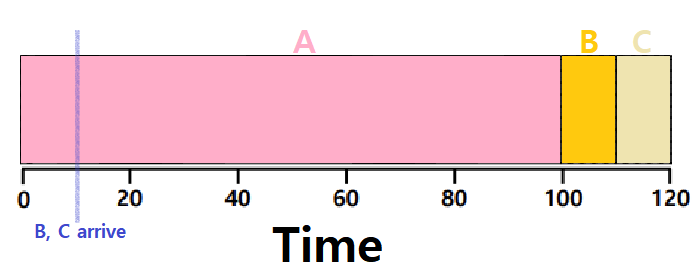
• 허나, 위 그림처럼, ABC 중 A가 먼저 도달하고, 잠시 뒤에 B와 C가 동시에 들어갔다고 해보자. A가 이미 CPU를 점유해버렸고, 이 Algorithm은 Non-Preemptive하기 때문에 또 Convoy Effect가 발생한다. ★

𝑨𝒗𝒆𝒓𝒂𝒈𝒆 𝒕𝒖𝒓𝒏𝒂𝒓𝒐𝒖𝒏𝒅 𝒕𝒊𝒎𝒆 = (𝟏𝟎𝟎 + (𝟏𝟏𝟎 − 𝟏𝟎) + (𝟏𝟐𝟎 − 𝟏𝟎)) / 𝟑 = 𝟏𝟎𝟑.𝟑𝟑
(B와 C가 10초 시점에 도달했다고 가정)

~> Average Waiting Time의 경우, (90+90+100)/3의 값을 가질 것!
~~> 여전히 문제가 있다!

  여기까지 놓고 보았을 때, 다음과 같은 생각이 충분히 들 것이다.

"그렇다면, 새 Process가 들어오는 시점마다 새 Process를 포함해 모든 Process 간에서 가장 짧은 Process를 택해서 수행시키면 되겠네?"

~> 이러한 Idea를 기반으로 시작한 Algorithm이 아래의 STCF이다.

STCF Algorithm

  'STCF(Shortest Time-to-Completion First) Scheduling Algorithm'은 Preemptive Algorithm이다. OS가 직접 CPU Control을 가져와서 재분배해야하기 때문이다.

'STCF = PSJF(Preemptive Shortest Job First) = SRTF(Shortest Remaining Time First)'

FIFO나 SJF와 다르게 Preemptive한 Algorithm이다.

Schedule the job that has the least time left !!

• Preemption(선매, 선점) 기능이 추가되었다. Process 수행 중간에 남은 부분을 냅두고 Suspend시킨 다음, 다른 Process를 수행시킬 수 있다는 것이다. ★

  앞서 SJF Algorithm의 단점을 소개할 때 들었던 예시 상황을 다시 상정해보자. 이번엔 STCF Algorithm이다. 아래와 같이 변화할 것이다.

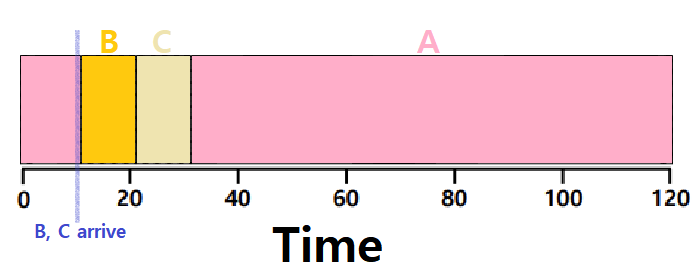
𝑨𝒗𝒆𝒓𝒂𝒈𝒆 𝒕𝒖𝒓𝒏𝒂𝒓𝒐𝒖𝒏𝒅 𝒕𝒊𝒎𝒆 = ((𝟏𝟐𝟎 − 𝟎) + (𝟐𝟎 − 𝟏𝟎) + (𝟑𝟎 − 𝟏𝟎)) / 𝟑 = 𝟓𝟎

~> 이러한 STCF Algorithm은 Scheduling의 Performance 측면에서 Optimal하다고 알려진다. 상시 가장 짧은 수행 시간의 Process를 채택하므로 자명하다.

하지만, 우리가 깔아놓은 가정을 잠시 돌이켜보자.

우리는 현재 Process들의 수행 시간을 미리 알 수 있다고 가정하고 있다.

허나, 실제 Process의 수행 시간을 아는 것이 과연 쉬울까?

실제로는, Process의 수행 시간을 정확히 아는 방법이 없는 경우가 많다.

=> 따라서, 실제 OS에서 이러한 STCF Algorithm을 적용하기 위해선 Process의 수행 시간을 예측할 수 있어야 한다. ★

Exponential Averaging

  SJF, STCF Algorithm은 Turnaround Time 측면에서 Optimal Algorithm이지만 우리가 CPU Burst의 길이를 알기 어렵다는 한계점에 봉착해있다.

• 하지만, 길이를 예측하는 몇 가지 테크닉이 있긴 하다.
  • 그 중 하나는 바로 Exponential Averaging이다.

• ※ Exponential Averaging
  • Previous Process의 CPU Burst 길이를 이용해 예측한다.
  • tn은 n번째 CPU Burst의 실제 길이이다. (과거의 Data)
  • τn+1은 그 다음 CPU Burst 길이의 예측 값이다. (τ: 타우)
  • α는 0 이상 1 이하의 가중치(Weight) 값이다.

Exponential Averaging : 앞선 Process의 CPU Burst 길이 tn과 앞선 Process에 대한 과거의 예측값 τn을 이용해 가중치를 활용하여 τn+1을 결정하는 것이다. ★

τn+1 = αtn + (1-α)τn

~> 만약, α가 0.5이고, 이전 예측값이 10, 실제가 6이었다고 하면, 다음 Process에 대한 예측값은 8이 되는 것이다. ★

~> α가 0이면 History과 고려되지 않고, 그냥 예측값이 고정되어 있는 것이다. ★★

~> α가 1이면 History만 고려해, 직전 CPU Burst 길이를 그대로 따라가는 것이다. ★★

  위의 τn+1 = αtn + (1-α)τn 공식을 다음과 같이 확장해보자.

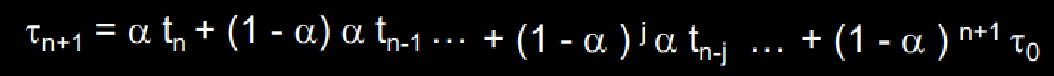
~> α와 (1-α)는 둘 다 0이상 1이하의 값이다. 따라서, 위의 확장식을 보면 Successor는 반드시 Predecessor보다 더 작은 Weight을 가진다는 것을 알 수 있다. (0~1)^k의 k가 계속 커지므로!
~~> 따라서, 실제 실험을 해보면 시간이 지날수록 Predict 값이 Real 값에 가까워지는 경향이 있다고 한다.

  금일 포스팅은 여기까지이다.