abstract

transformers는 잠재적인 장기의존성을 가지고 있다. 하지만 모델링에서 고정 길이 세팅으로 제한이 있었다. transformer-xl은 이전 segment를 처리할 때 계산된 hidden state들을 사용하는 recurrence mechanism을 적용하고 이에 맞는 새로운 positional encoding을 도입해 한계를 극복했다.
이 방법은 RNN보다 지난 text의 80% 의존성을 학습 가능하게 하였고 context fragmentation 문제도 해결했다. 또한 vanilla transformers보다 1800+ 속도 빠르게 평가가 가능해졌다.

이전 모델들의 한계

RNN

• Gradient vanishing , exploding problem
  오차 역전파과정에서 전달되는 gradient의 크기가 기하급수적으로 작아져 optimal solution의 방향을 지시하는 기능을 상실하게되는 Vanishing gradient현상 발생. 역전파과정에서 gradient가 기하급수적으로 커져 결국 NaN값이 되고 더는 학습을 진행할 수 없는 상태가되는 Exploding gradient 문제 발생.

장기의존성이란?
예문 ) "나는 그제 가족과 함께 광화문 광장에서 즐겁게 놀았다"

이 문장의 핵심인 '나는'과 '놀았다'는 7이라는 시간 차이를 두고 서로 의존성을 갖는다.
시퀀스 데이터에서 요소들은 각기다른 시간 차이를 두고 서로 관련성을 갖고있다. 관련된 요소가 멀리 떨어져 있는 경우 시퀀스에 장기 의존성이 존재한다고 한다. 이런 시퀀스 데이터는 장기 의존성이 필요한데, 단어간의 사이가 멀어질수록 잘 기억을 하지 못하는 문제가 있다.

LSTM

• LSTM에는 RNN과 다르게 이전 정보를 지속해서 흘려주는 Cell State와 불필요한 정보를 걸러주는 Gate가 존재해서 gradient vanishing and explosion을 해결(예방)한다. 하지만 LSTM은 평균적으로 200개의 단어만 사용하여 한계 존재.

TRANSFORMER

• Self attention을 활용하여 각 token이 최단거리로 연결되어 long-term dependency 문제 해결한다.
• context fragmentation
  segment들은 문장의 구분, 의미적인 구분이 없이 단순하게 character의 개수를 기준으로 분리되었다. 이로 인해 한 segment 안에서, 처음 몇 개의 character를 예측할 때 사용할 수 있는 정보들이 별로 없다. 이 문제를 저자들은 'context fragmentation'이라고 부른다.

이전 transformer 구조와 비교

이전 transformer 구조

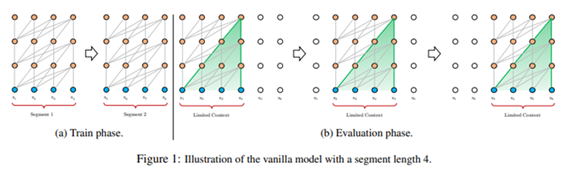
문제 1.  segment 크기를 넘어서는 long-term dependency를 학습할 수 없다.

학습단계에서 고정크기 가진 모델 학습시킨 후 평가 단계에서 고정크기를 사용한다.
앞서 말한 것과 같이, 고정된 segment단위로 학습하면, segment 크기를 넘어서는 long-term dependency를 학습할 수 없고, 문장이나 의미를 고려하지 않고 segment가 나눠지는 'context fragmentation' 문제가 발생한다. x2~x5 평가할 때 x1반영못하는 것을 볼 수있다. 이처럼 평가단계에서도 고정크기를 사용하여 앞, 뒤 정보를 무시하는 상황이 나온다.

문제 2. prediction을 수행할 때 중복된 연산이 많아진다.

Prediction 단계에서는 한 segment를 이용하여 segment의 맨 마지막 한 개의 위치에 올 token만 예측하게 된다. [x1, x2, ... xt-1]을 이용하여 xt를 예측한다.
그리고 segment를 한 칸 옆으로 이동하여 그 다음 위치에 올 token을 예측하게 되는데 [x2, x3 .. xt]을 이용하여 xt+1을 예측, 이 때 겹치는 token들에 대한 연산을 다시 수행해야 한다. 따라서 중복된 연산 많아진다.

transformer-XL 구조 : segment level recurrence mechanism

개선방법 : Hidden state를 사용하여 이전보다 긴 long-term dependency 학습!

이에 저자들은 현재 segment를 처리할 때, 이전 segment를 처리할 때 계산된 hidden state들을 사용하는 recurrence를 추가하여 이런 문제을 해결하고, 그에 맞게 positional encoding을 변형하였다.

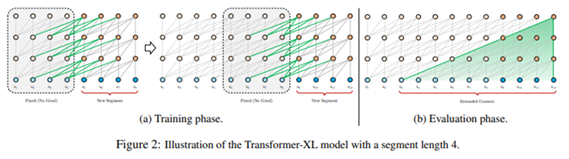
• 이전 segment를 처리할 때 계산된 hidden state를 사용한다. 이전 segment의 hidden state를 활용하면 이전보다 더 긴 long-term dependency를 학습할 수 있게 된다. 첫번째 그림에서, x5 시점에서 다음을 예측할 때 x2, x3, x4의 hidden state들을 활용하는 것을 볼 수 있다. Recurrence 메카니즘이 없었다면 x5의 input만 참고하여 예측했을 것이다.

• 이전 segment의 hidden state들이 다음 segment를 처리하기 위해 사용될 때는 gradient에 따라 학습시키지 않고 고정시킨다. 이 때 학습되는 weight들은 현재 segment에 속한 weight들 뿐이다.

• 이런 recurrence 메커니즘은 segment 단위의 recurrence를 만들어낸다. 그래서 필요한 context가 두 개의 segment를 넘어서서 여러 segment에 걸쳐 전파될 수 있다.
  Prediction 시, 이전 segment의 계산 결과를 저장해놓고 활용할 수 있기 때문에 매번 다시 계산할 필요가 없어진다.
  실제로 enwiki-8 데이터를 사용한 실험에서 vanilla 모델보다 1800배 이상 빠른 속도를 보여줬다.

relative positional encodings 필요성

Transformer 구조에 recurrence 메카니즘을 적용하면 transformer 구조에 사용되는 포지션 정보를 어떻게 추가할 것인가 하는 문제가 발생한다. 이전 segment에 사용된 포지션 정보가 현재 segment에도 변함없이 동일하게 적용되기 때문에 이전 segment의 첫번째 input에 더해진 포지션 정보와 현재 segment의 첫번째 input에 더해진 포지션 정보가 같다.

이 문제를 해결하기 위해 기존의 'absolute' 포지션 정보가 아닌 'relative' 포지션 정보를 준다. 'Absolute' 포지션 정보는 현재 input token의 절대적 위치 예를들어 첫번째, 20번째 같은 위치 에 대한 정보를 의미하며, 이 포지션 정보는 두 token 간의 attention을 계산할 때 활용된다.

absolute positional encodings

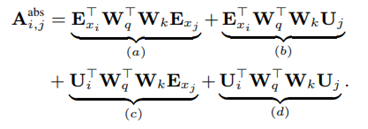
Query인 Q와 Key인 K 사이의 attention 계산 : Q^T K
Q = (E + U) Wq
K = (E + U) * Wk
E는 토큰 임베딩 U는 포지션 정보
U에 인코딩된 i번째, j번째 absolute 포지션 정보을 통해 두 단어 간의 위치 차이를 반영한다.

relative positional encodings

'Absolute' 포지션 정보가 두 수의 차이를 계산하기 위해 a=1, b=2 이렇게 값을 지정하고 그 값으로 차이를 계산하는 방식이라면, 'relative' 포지션 정보는 두 수의 값과는 상관없이 두 수의 차이 값만 갖고 있는 방식이다. a=1, b=2이든 a=5, b=6이든 상관없이 두 수(위치)의 차이가 1이라는 것만 알려주면 된다. 이 방식을 이용한 attention 계산을 수식으로 나타내면 아래와 같다.

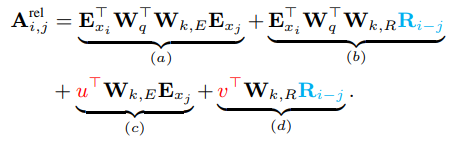
R이 'relative' 포지션 정보를 encoding한 matrix를 가리키며 기존에 쓰이던 U를 대체한다.
i, j 두 위치의 차이에 대한 포지션 정보를 담고 있다. 추가적으로 벡터 형태의 u, v 파라미터가 도입, 두 벡터는 query 단어의 위치와 상관없이 같은 값을 갖는다.(고정값)

Wk를 W_k,E와 W_k, R로 분리한다.
W_k,E는 token의 임베딩을 이용한 attention 계산에 쓰이고, W_k,R은 상대 위치 정보를 반영한 attention을 계산할 때 쓰인다.

그리고 R은 'Attention is all you need'에서 제안한 방식대로 학습되는 matrix가 아닌 sinusoid encoding matrix를 그대로 사용한다.

• 최종적인 계산과정
  

결과

평가지표 : PPL
문장의 발생 확률이 높을수록 해당 문장에 대한 Perplexity 값은 낮아짐!

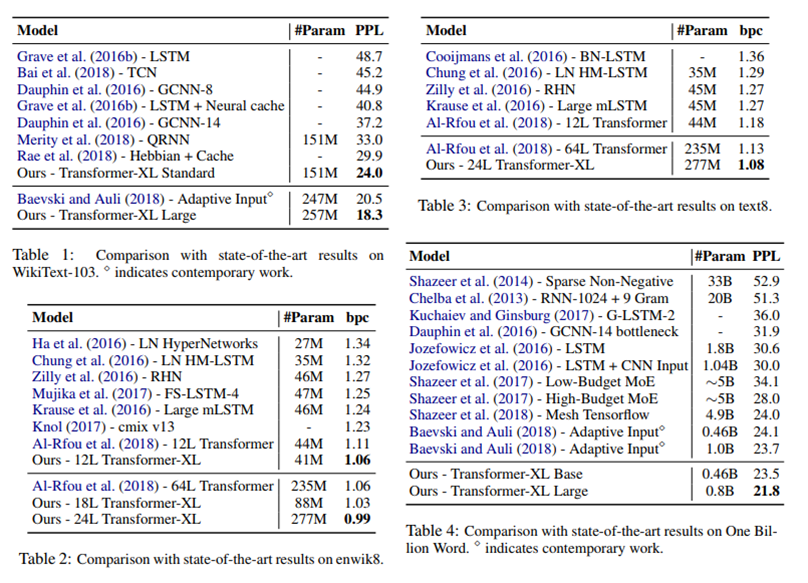
여러 데이터를 이용한 word-level, character-level language modeling에서 sota를 기록함. long-term dependency가 없는 One Billion Word dataset(table 4)에서도 가장 좋은 성능을 기록한 것이 인상적이다.

참고

논문 : Transformer-XL

블로그