<사전 이해>
LIME, Filter Visualization와 같은 피처맵 시각화 방식은 모델이 입력 이미지에 어떻게 반응하는 지 각 은닉층을 조사하는 방법이다. 하지만 이는 깊은 은닉 계층일수록 해석력이 떨어지고, 해석자마자 모델을 다양하게 받아들일 소지가 여전히 존재한다.
LRP(Layer-wise Relevance Propagation)은 딥러닝 모델의 결과를 역추적해서 입력 이미지에 히트맵을 출력한다. 히트맵은 블랙박스가 데이터의 어느 곳을 주목하는지 표시할 수 있기 때문에 피처맵 기법보다 블랙박스를 오인할 가능성이 적다. LRP는 이러한 히트맵 방식 XAI 기법 중 가장 대표적인 방식이다.
LRP는 아래와 같이 크게 두 가지 기법으로 혼합되어 있다.

1. 타당성 전파(Relevance Propagation, RP): 특정 결과가 나오게 된 원인을 분해하고, 비중을 분배하는 과정

2. 분해(Decomposition): 타당성 전파를 통해 얻어낸 ‘원인’을 가중치로 환원하고 해체하는 과정

필터 시각화나 민감도 기법은 딥러닝 모델에서 순 방향으로 진행(feed-forward)하며 데이터 흐름을 관찰하는 기법이다. LRP는 이와 반대로 블랙박스가 분류한 이미지 결과를 역순으로 탐지하며 분해하고, 분해된 요소들이 원본 이미지까지 도달했을 때 원본 이미지에 상대적인 기여도를 표시함으로써 딥러닝 모델을 해석한다.
LRP는 딥러닝 모델을 역순으로 탐지하기 위해 분해(Decomposition) 기법을 사용하고, 기여도를 계산할 때는 타당성 전파(Relevance Propagation)를 사용한다.

Decomposition
분해는 간단히 말하면 입력된 피처 ‘하나’가 결과 해석에 얼마나 영향을 미치는지 해체하는 방법이다. 예를 들어, 어떤 이미지 x에서 픽셀 k가 결과를 도출하는 데 도움이 되는지(+), 해가 되는지(-)를 알아낼 수 있다. 예시) LRP의 분해 과정에서는 이미지를 '고양이' 로 예측할 가능성에서부터 딥러닝을 역방향으로 순회하며 각 은닉층의 결과 기여도를 판단한다.

Relevance Propagation
분해 과정을 마친 은닉층이 결과값 출력에 ‘어떤 기여’를 하는지 타당성을 계산하는 방법이다. 타당성 계산으로 모든 은닉층 내 활성화 함수의 기여도를 계산할 수 있다면, 이미지 x에서 픽셀 별 기여도를 표시할 수 있다.

• 딥 테일러 분해
  위에서 아래와 같은 식이 성립함을 알 수 있다.
  f (x )=f (a )+∑p =1 d ​∂x p ​∂f ​∣x =a ​(x −a )+ϵ
  이 때, f (a )=0 ,ϵ=0일 때 relevancies를 계산할 수 있다.
  f (x )=f (a )+∑i =1 d ​∂x i ​∂f ​∣x i ​
  =a i ​​(x i ​−a i ​)+ϵ=∑i
  =1 d ​∂x p ​∂f ​∣x
  =a ​(x −a )=∑i
  =1 d ​R i ​
  즉, 출력을 Relevancy Score만으로 분해하자.

딥테일러분해 설명 블로그

Abstract

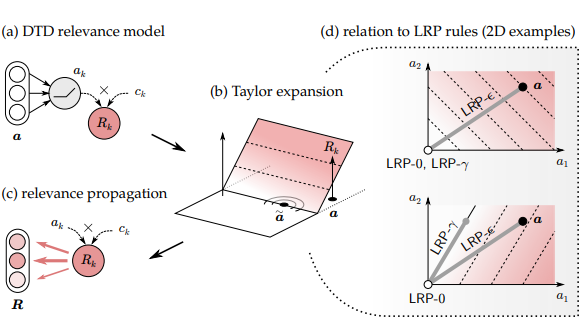
기계 학습 모델이 잘 일반화되기 위해서는 입력 데이터의 의미 있는 패턴에 의해 결정이 뒷받침되도록 해야 한다. 그러나 사전 요구 사항은 모델이 예를 들어 예측을 지원하는 데 사용하는 입력 기능을 강조함으로써 자신을 설명할 수 있어야 한다. 계층별 관련성 전파(LRP)는 그러한 설명 가능성을 제공하고 잠재적으로 매우 복잡한 심층 신경망으로 확장되는 기술이다. 의도적으로 설계된 전파 규칙 집합을 사용하여 신경망에서 예측을 역방향으로 전파함으로써 작동한다. 이 장에서는 (1) 전파 규칙을 쉽고 효율적으로 구현하는 방법, (2) 전파 절차를 '딥 테일러 분해'로 이론적으로 정당화할 수 있는 방법, (3) 높은 설명 품질을 제공하기 위해 각 계층에서 전파 규칙을 선택하는 방법 및 (4) LRP가 할 수 있는 방법에 대한 논의를 통해 LRP에 대해 간략하게 소개한다. 심층 신경망을 넘어 다양한 기계 학습 시나리오를 처리할 수 있도록 확장된다.

10.1 introduction

대규모 데이터셋은 종종 잘못된(가짜) 상관관계로 입력 변수 중 어떤 것을 사용해야 하는지 결정해야 할 때 학습 기계를 당황하게 만든다. feature selection은 제한된 수의 좋은 input feature를 제시함으로써 잠재적인 해결책을 제공한다. 그러나 이 접근법은 개별 픽셀의 역할이 고정되어 있지 않은 이미지 인식에서 적용하기가 어렵다.
그래서 다른 방향으로 이 문제에 접근한다.

첫째로, 모델은 feature selection에 너무 큰 신경을 쓰지 않고 학습시킨다. 신경망이 학습한 후에 입력 features를 보고, ‘bad’ feature을 지우고 다시 cleaned data로 학습할 수 있다. 간단한 방법인 테일러 분해는 근처 기준점 에서 예측 f(x)의 테일러 확장을 수행하여 설명할 수 있다.

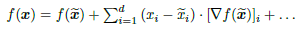
단순하고 간단하지만, 이 방법은 심층 신경망에 적용될 때 불안정하다.
1. 함수 기울기에 노이즈가 많다.
2. 작은 변화로 f(x)는 급격하게 바뀔 수 있다. 등등

더 나은 해결책을 위해 수많은 설명 기법이 제안되었다.

1. 지역 경사 추정치를 통합하여 설명을 개선한다.
2. 좀 더 거친 기울기 추정치를 사용한다.

10.2 Layer-Wise Relevance Propagation

• LRP는 설계된 로컬 전파규칙을 통해 신경망에서 예측 f(x)를 역방향으로 전파함으로써 작동한다. LRP에 의해 구현된 전파 절차는 보존 특성에 따라 같은 양으로 하위 계층에 재배포 되어야한다.
• 주어진 레이어에서 관련성 점수(Rk) k를 하위 레이어의 뉴런으로 전파하는 것은 다음과 같은 규칙을 적용하여 달성된다.

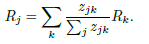
z(jk)는 뉴런 j가 뉴런k를 연관시키는데 기여한 정도를 모델링한다. 분모는 보존 속성을 적용하는 역할을 한다.
입력 feature에 도달하면 전파 절차가 종료된다. 네트워크의 모든 뉴런에 대해 위의 규칙을 사용하면 레이어별 보존 특성을 쉽게 확인할 수 있다. LRP는 단순한 테일러 분해 접근법과 다르다.

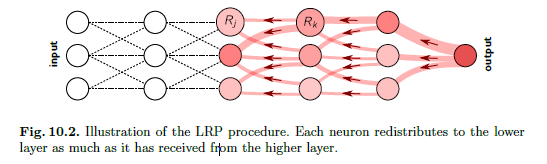
각 뉴런은 상위 계층으로부터 받은 양만큼 하위 계층으로 재분배된다.

LRP는 흔히 사용되는 ML 모델과 데이터셋에 bias와 insight를 찾기위해 적용된다.

10.2.1 LRP Rules for Deep Rectifier Networks

• basic rule : 이 규칙은 Eq에서 발생하는 뉴런 활성화에 대한 각 입력의 기여도에 비례하여 재배포된다. 하지만 심층 신경망의 기울기는 일반적으로 노이즈가 많으므로 더 강력한 전파 규칙을 설계해야 한다.
  

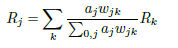
• epsilon rule : 분모에 값 추가. e를 추가하여 뉴런 활성화에 기여할 때 어느정도 relevance를 흡수한다.

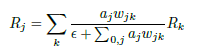
• Gamma Rule : 또 다른 개선사항으로, 부정적인 기여보다 긍정적인 기여의 효과를 얻도록 수정한다. 모수 γ는 얼마나 많은 양의 긍정적인 기여를 선호하느냐에 따라 조절된다. γ가 증가함에 따라 부정적인 기여는 사라진다.

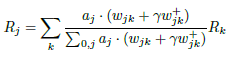
10.2.2 Implementing LRP Efficiently

앞서 소개한 LRP 규칙 구조는 쉽고, 효율적이다. LRP-0/e/γ를 고려한 경우에는 4단계로 분해되어 설명한다.

10.2.3 LRP as a Deep Taylor Decomposition

전파규칙은 딥 테일러 분해로 해석된다.

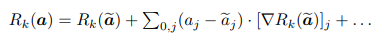
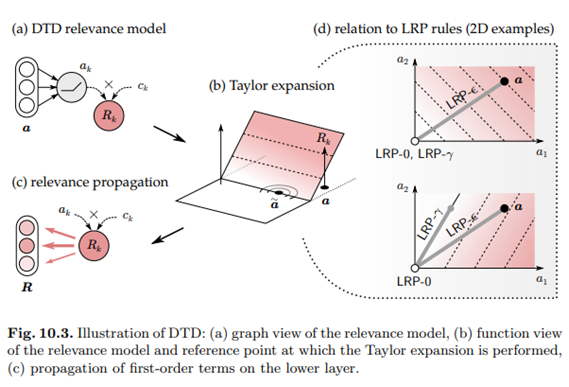
1차 항은 하위 계층의 뉴런에 얼마나 많은 Rk가 재배포되어야 하는지를 식별한다. a와 Rk 사이의 잠재적인 복잡한 관계 때문에, 적절한 기준점을 찾고 국소적으로 기울기를 계산하는 것이 어렵다. 그래서 실제 관련 함수 Rk(a)를 분석하기 쉬운 관련 모델로 대체할 필요가 있다. 그러한 모델 중 하나는 변형된 ReLU 활성화함수이다.

2차 및 고차 항은 ReLU 함수의 선형성으로 인해 0이다. 0차 항은 ReLU 힌지 근처의 기준점을 선택하여 임의로 작게 만들 수도 있다. 기준점이 선택되면 1차 항을 쉽게 계산하고 하위 계층의 뉴런으로 재배포할 수 있다. 그림 10.3(a-c)은 주어진 뉴런에서 테일러 분해가 얼마나 깊이 적용되는지를 보여준다.

10.3 Which LRP Rule for Which Layer?

전파를 위한 일반적인 프레임워크로서, LRP는 각 계층에서 사용할 규칙과 매개 변수 e와 y를 어떻게 설정해야 하는지에 대해 유연하게 만든다.

LRP 매개 변수를 최적으로 선택하려면 설명 품질을 정해야한다. 충실도와 이해성 즉, 설명은 관심 있는 출력 뉴런을 정확하게 표현해야 하며, 인간을 위해 해석하기 쉬워야 한다.
설명의 충실도를 시각적으로 평가하려면 올바른 visual feature를 사용하여 예측하고 이미지의 방해되는 요인을 무시해야 한다.

• 그림 10.4는 주어진 입력 이미지(크기 224 x 224), VGG-16 출력 뉴런 'castle'에 대한 다양한 LRP 설명을 보여준다.

우리는 explanation의 강한 차이를 확인할 수 있다. Uniform LRP-0은 기능의 많은 로컬 artifact를 선택한다. 설명은 지나치게 복잡하며 이미지의 실제 castle에 충분히 초점을 맞추지 않는다.

Uniform LRP-e는 설명에서 노이즈 요소를 제거하여 이미지의 실제 성과 일치하는 제한된 수의 feature만 유지한다.

균일한 LRP-r는 feature가 더 자세히 강조되기 때문에 인간이 이해하기 쉽지만, lamp post와 같은 관련이 없는 개념을 선택하여 불충실하게 만든다.

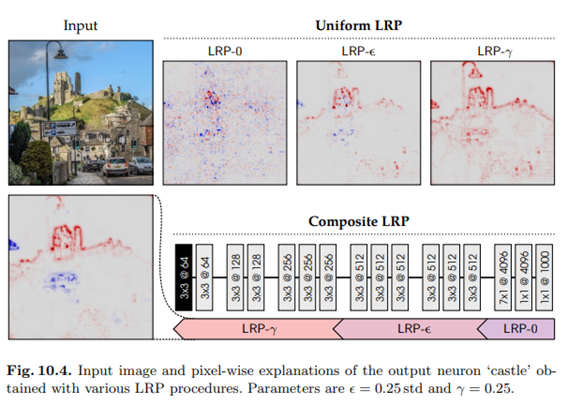
복합 LRP는 위의 접근 방식의 단점을 극복한다. 성의 특징은 올바르게 식별되고 완전히 강조되어, 따라서 설명을 충실하고 이해할 수 있다.

복합 LRP가 더 나은 설명을 제공하는 이유는 VGG-16 신경망의 다양한 계층 간의 quality를 추적하며 알 수 있다.

• upper layers

상위 계층에는 약 4,000개의 뉴런(즉, 클래스당 평균 4개의 뉴런)만 있기 때문에 서로 다른 클래스를 구성하는 많은 개념들이 얽혀 있을 가능성이 있다. 여기서 함수와 그 기울기에 가까운 전파 규칙(예: LRP-0)은 이러한 얽힘에 민감하지 않을 것이다.

• Middle layers

중간 레이어는 더 얽힌 표현을 가지고 있지만, LRP-γ는 이러한 가짜 변이를 걸러내고 가장 두드러진 설명 요인만 유지한다.

• Lower layers

하위 레이어는 중간 레이어와 유사하지만, LRP-γ는 모든 개별 픽셀의 기여를 포착하기보다는 전체 feature로 일관되게 relevance를 spread하는 경향이 있기 때문에 LRP-γ가 더 적합하다. 이것은 인간이 더 쉽게 이해할 수 있도록 설명을 만든다.

10.3.1 Handling the Top Layer

• sequence of layer를 설명할 수 있는 수식

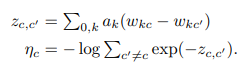
< 풀링 계층에 대한 전파 규칙 >
첫 번째 계층은 로그 확률비 log[P(ωc)/P(ωc’)]를 나타낸다.
두 번째 계층은 이러한 비율에 대해 역 log-sum-exp 풀링을 수행한다.
이를 통해 만들어진 점수는 일반적인 LRP 규칙을 사용하여 신경망으로 더 전파될 수 있다.

10.3.2 Handling Special Layers

실용적인 신경망은 종종 특수 레이어를 갖추고 있다. 특수 레이어는 최적화, 사전 정의된 불변성을 모델에 통합하거나 특정 유형의 입력 데이터를 처리한다.

<LRP 프레임워크 내에서 이러한 계층 중 일부를 처리하는 방법>

최대 풀링 계층은 승자독식 재배포 방식(a winner-take-all redistribution scheme)으로 처리되거나, sum-pooling case와 동일한 규칙을 사용하여 처리될 수 있다.

배치 정규화 계층은 일반적으로 training을 용이하게 하고 예측 정확도를 높인다. 테스트 시 , 단순히 스케일 조정 및 크기 조정 작업을 수행한다. 따라서 이러한 층들은 함수를 변경하지 않고 인접한 선형 층에 의해 흡수될 수 있다. 이를 통해 LRP 적용에 필요한 표준 신경망 구조를 복구할 수 있다.

입력 계층은 ReLU 활성화함수를 입력으로 받지 않고 픽셀 또는 실제 값으로 받기 때문에 중간 레이어와 다르다.
이러한 계층에 대한 특수 규칙은 DTD 프레임워크 에서도 도출할 수 있다. 이 장에서는 픽셀에 적합한 zB-규칙을 사용했다.

10.4 LRP Beyond Deep Networks

Unsupervised Models
비지도학습 알고리즘은 라벨없는 데이터에서 추출한 구조로 cluster 어느 정도 예측할 수 있다. 이러한 예측 결과를 설명하기 위해 새로운 방법론이 제안되었다.

time seires prediction
인기있는 모델은 LSTM, 이러한 모델에 LRP를 적용하는 성공적인 전략은 두 번째 term을 통해 모든 관련성이 흐르도록 하는 것이다. g가 ReLU 함수로 선택되고, 게이트 함수가 엄격하게 긍정적이거나 국소적으로 일정하다면, 이 전략은 DTD 프레임워크 내에서 정당화될 수 있다.

10.5 Conclusion

전파 규칙을 통해 네트워크에서 예측을 역방향으로 전파함으로써 입력 feature 측면에서 복잡한 SOTA 신경망의 예측을 설명할 수 있다.
전파 규칙은 대부분의 현대 신경망 소프트웨어에서 효율적이고 모듈식으로 구현될 수 있으며 이러한 규칙 중 일부는 딥 테일러 분해 프레임워크에 더 많이 embeddable하다. LRP 규칙의 매개 변수는 복잡한 모델에 대해서도 높은 품질의 설명을 얻는 방식으로 설정할 수 있다. 마지막으로, LRP는 심층 신경망 분류기를 넘어 더 광범위한 기계 학습 모델과 작업으로 확장 가능하다. 이를 통해 설명이 필요한 많은 실제 시나리오에 적용할 수 있다. 학습된 비지도 모델은 먼저 '신경화'(즉, 기능적으로 동등한 신경망으로 변환)된다. 그런 다음 신경망에서 예측을 역방향으로 전파하기 위해 LRP 절차를 이용한다.

논문 : Layer-Wise Relevance Propagation: An Overview