VAE는 처음부터 auto encoder구조를 염두해두고 만들어 진게 아니다.
뒷단, 즉 deterministic한 generator부분의 분포를 학습시키려다 보니까 앞단이 붙은거고 공교롭게 그 구조를 보니까 auto encoder와 똑같아진 경우임
우린 Generative model을 control 하고 싶어한다.
( latent vector 조금 바꾸면 성별이 바뀐다거나 )
z => controller

생성 모델의 목표는 단순히 데이터를 잘 설명하는 분포를 찾는 것뿐만 아니라, 새로운 데이터를 생성할 수 있는 모델을 만드는 것이기 때문에 p(x) 분포를 찾는 것이 중요함 (이 분포는 매우 복잡하다)
z가 컨트롤러라 했으니까 z의 분포가 우리가 만지기 쉬운 분포면 편하겠다 => p(z)를 가우시안 으로 두자
엥?
z 는 manifold 공간에서의 값인데 그냥 가우시안 분포로 퉁쳐서 유클리드 거리 가까운 애 위주로 샘플링 하는건 아니지 않아? manifold 면을따라서 샘플링을 하던가 해야될거 아니야
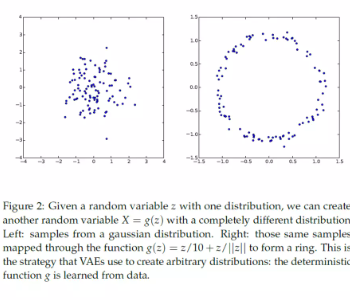
좋은 지적이다!
그러나 이렇게 해도되는 이유는 이후에 이어지는 몇개의 디코더 layer에서 알아서 딱 맞는 latent space로 (원래의 맞는 분포로) 맵핑을 해준다고 한다.
그걸 증명한 논문도 있음
p(x)를 가우시안으로 두고 MLE하면 안됨 근데
MSE가 적어도 의미적으로 멀 수 있다.
왜 이런일이 발생하는가?
p(x)분포는 생각보다 복잡하기 때문이다. (manifold를 생각해보자)
가우시안 기각당함. 자 정리해보자
우리는 네트워크의 출력이 training sample과 가깝길 바란다.
그 의미적으로 가까운 애들이 나오게 하는 z , 그 z를 샘플링할 수 있는 이상적인 샘플링 함수 p(z|x) 의 분포를 구하는 행위를 할 것이다.
" 내가 x를 보여줄테니 적어도 이 x는 잘 나타내는 z의 분포를 구해보자 ( p(z|x)) z를 잘 만들었으면 x를 다시 generate하는 것도 어렵지 않을거야"
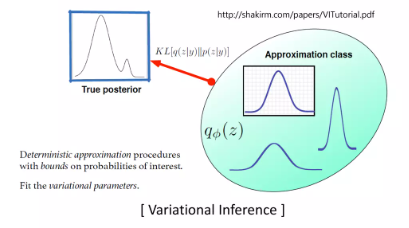
근데 p(z|x)도 모름 => Variational Inference 사용
다루기 쉬운 qØ (z|x) 로 approximation 하는 것

최종식을 직관적으로 이해해보자면
- p (z|x)를 근사하는 q(z|x)가 p(z) 과의 KL다이버전스가 작으면 바라는 바, 더할나위 없고
- p(x|z)값이 높다는건 잘 생성된 z로 x를 다시 잘 생성해낸다라는 뜻
곧 잘 우리의 목적과 부합한다.

두번째 Derivation도 있는데
아까 ELBO 나왔던 식 maximize하는거는 똑같고 KL 다이버전스를 줄여야 p(x) 분포 잘 구할 수 있겠지?
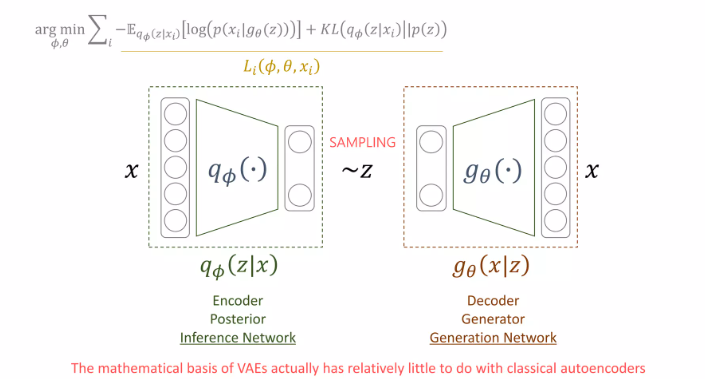
그랬더니 auto encoder더라~

좀 더 자세히 살펴보면 다음과 같다.
LOSS function 계산
KL divergence

p(z)도 정규분포 가정
KL term은 계산이 쉽게 된다.
Reconstruction Error

Monte-carlo technique을 사용해서 적분식으로 바꾼다음 L값을 무수히 많이 해서 시그마로 근사한다.
각 x값 하나당 다른 z분포가 생성되고 그 분포당 L개의 샘플링을 함
sampling하는 과정은 어떻게 back-prop하지?

이렇게~
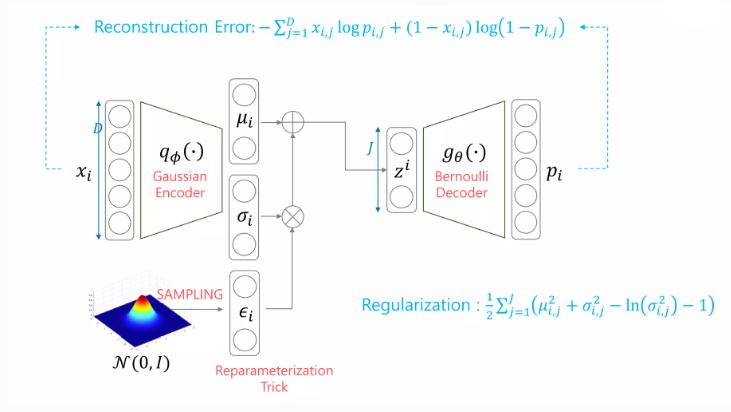
generator 부분의 conditional probability distribution을 베르누이를 가정함 =>cross entropy Loss 가 된다.

