다익스트라 알고리즘을 활용한, 방향 그래프에서의 최소 거리비용(최소 힙 priority queue 사용) in C++

임의의 정점에서 출발한다고 가정할 때, 방향 그래프 내에서 각 정점으로 가는 최소 거리비용을 출력하는 코드

임의의 정점은 1번 정점으로 한다.
정점의 수 n, 간선의 수 m이 주어진다.
각 간선은, 출발 정점, 도착 정점, 비용을 입력으로 받는다.

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

struct Data {       // array of array
    int e, dis;
    Data(int a, int b ){
        e = a;
        dis = b;
    }
    bool operator< (const Data &d) const {
        return dis > d.dis;
    }
};

int n, m;
vector<int> dist(21, 2147000000);
vector<Data> graph[21];
priority_queue<Data> pQ;

int main() {
    freopen("input.txt", "rt", stdin);
    cin >> n >> m;
    for (int i=1; i<=m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        graph[a].push_back(Data(b, c));
    }
    pQ.push(Data(1, 0));        // 임의의 시작점
    dist[1] = 0;
    while(!pQ.empty()) {
        Data data = pQ.top();
        int now = data.e;
        int dis_sum = data.dis;
        pQ.pop();

        for(int i=0; i<graph[now].size(); i++) {
            int next = graph[now][i].e;
            int next_dis_sum =  dis_sum + graph[now][i].dis;
            if(dist[next] > next_dis_sum) {     // relaxing
                dist[next] = next_dis_sum;
                pQ.push(Data(next, next_dis_sum));
            }
        }
    }
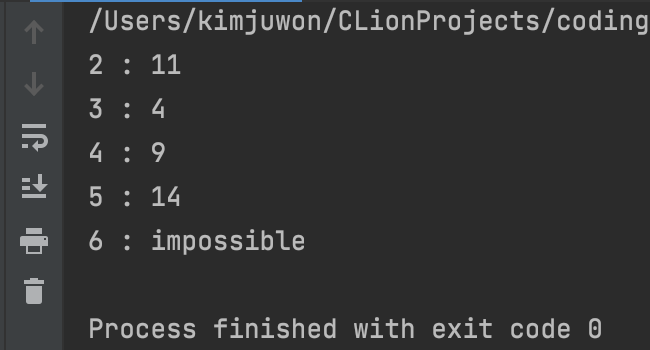
    for(int i=2; i<=n; i++) {
        if(dist[i] != 2147000000) cout << i << " : "
        << dist[i] << '\n';
        else cout << i <<" : can not reach\n";
    }
    return 0;
}

임의의 정점에서 시작한다고 가정한다.
해당 정점에서 최소의 간선비용을 찾아, 해당 도착 정점으로 이동할때 값이 더 작다면 간다.

• vector dist : 해당 정점에 도착했을 때의 총 비용 기록
• vector graph : 방향 그래프
• priority_queue pQ : 최소의 간선비용을 찾는데 사용하는, 우선순위 큐
• if(dist[next] > next_dis_sum) : 총 비용의 값이 적어지는 경우에만 해당 정점을 방문한다
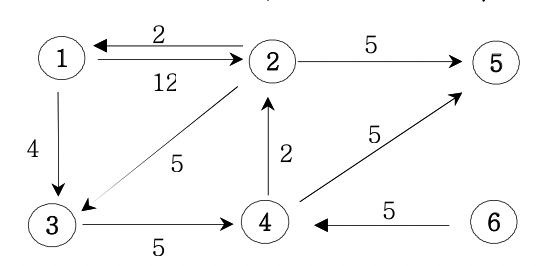
  ex)
  6 9
  1 2 12
  1 3 4
  2 1 2
  2 3 5
  2 5 5
  3 4 5
  4 2 2
  4 5 5
  6 4 5
  
  

다익스트라 알고리즘 활용시 특징

• 가중치가 음수인 경우에는 사용이 불가능하다. (값이 계속해서 realxing 되기 떄문에, 무한 루프를 돌게 된다.)
• 다익스트라 알고리즘이, 벨만포드 알고리즘 사용 시보다 속도가 빠르다.