벨만포드 알고리즘을 활용한, 방향 그래프에서의 최소 거리비용

방향 그래프에서, 특정 정점에서 다른 정점까지의 최소비용을 출력하는 코드

정점의 수 n, 간선의 수 m이 주어진다.
마지막 입력으로는, 알고자하는 비용의 구간인 출발 정점과 도착정점이 주어진다.
음의 사이클이 존재하여 답이 나올 수 없는 경우에는 -1출력.

#include <iostream>
#include <vector>

using namespace std;

struct Data {
    int s, e, val;
    Data(int a, int b, int c) {
        s = a;
        e = b;
        val = c;
    }
};

int n, m, answer_s, answer_e;
int dist[101];
vector<Data> graph;

int main() {
    freopen("input.txt", "rt", stdin);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        graph.push_back(Data(a, b, c));
    }
    for (int i = 1; i <= n; i++) {
        dist[i] = 2147000000;       // 무한대로 초기화
    }
    cin >> answer_s >> answer_e;
    dist[answer_s] = 0;     // 출발 정점
    for (int i = 1; i < n; i++) { // 간선 i개로 가는 경우를 말한다.
        for (int j = 0; j < graph.size(); j++) {
            int s = graph[j].s;
            int e = graph[j].e;
            int val = graph[j].val;
            if (dist[s] != 2147000000 && dist[s] + val < dist[e]) {
                dist[e] = dist[s] + val;
            }
        }
    }
    for (int j = 0; j < graph.size(); j++) {
        int s = graph[j].s;
        int e = graph[j].e;
        int val = graph[j].val;
        if (dist[s] != 2147000000 && dist[s] + val < dist[e]) {
            cout << "-1\n";
            return 0;
        }
    }
    cout << dist[answer_e];
    return 0;
}

• dist[i] : 출발정점에서 i번째 정점까지의 비용을 기록한다.

• dist[i] = 2147000000 : relaxing을 하기 위해서, 초기값을 무한대 값으로 한다.

• for (int i=1; i<n; i++) { for(int j=0; j<graph.size(); j++)} : 변수 i에 해당하는 for-loop는, 출발 정점에서 간선 i개로 도달할 수 있는 정점을 기록한다.
  
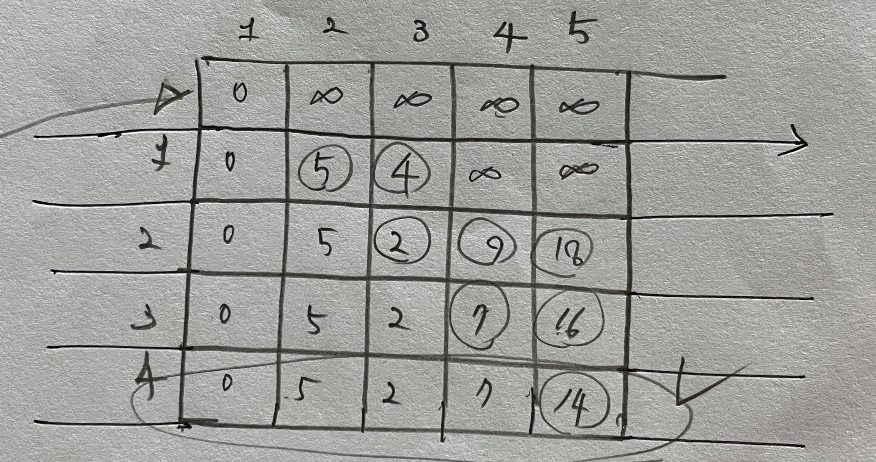
  즉 간선 1개부터, n-1개를 이용하는 경우의 수를 모두 기록한다.

• 맨 아래의 마지막 for(int j=0; j<graph.size(); j++) : 간선 n개를 이용하는 경우의 수이다. 이때 만약 realxing에 해당하는 값이 있다면, 이는 음의 사이클을 형성하는 부분이므로, -1을 출력하게 한다.

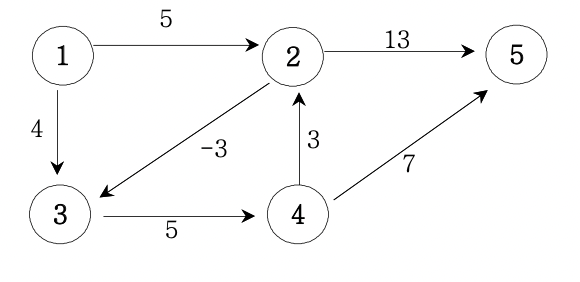
ex)
5 7
1 2 5
1 3 4
2 3 -3
2 5 13
3 4 5
4 2 3
4 5 7

1 5

벨만 포드 알고리즘의 특징

• 다익스트라 알고리즘의 경우, 간선이 음수인 경우에는 사용이 불가능하다.
• 벨만포드 알고리즘의 경우, 간선이 음수인 경우에도 사용이 가능하다.
• 다익스트라 알고리즘이, 벨만포드에 비해 속도가 느리다.