- 출처: 한기영(data insight)
Why Numpy?
-
데이터 분석시에는 대용량 데이터를 처리하곤 하는데, 이때 list는 느리다!
-
배열을 효과적으로 관리하고 싶다.
-
다차원 행렬 자료구조인 ndarray를 통해 벡터 및 행렬을 사용하는 선형 대수 계산에서 주로 사용
so, Numerical Python!
-
불러오자
import numpy as np
# 이때 함수를 쓰려면.. # np.함수명
# 또는 특정 함수만 불러오고 싶다면?
from numpy import array함수 vs 메서드
함수
: np.함수()
- 예: np.mean(): np array로 변환해서 평균을 구해 줌
메서드
: 특정 변수(데이터, 오브젝트)에 딸려 있는 함수!!!
: 변수명.메서드()
- 예: a.mean(): a가 np array일 때 사용 가능. 안그러면 에러남.
Numpy와 dnarray
numpy dnarray 만들기
: np.array()
a = np.array([1, 2, 3])
print(a) # [1 2 3] # 콤마가 없음!
print(type(a)) # <class 'numpy.ndarray'>
# 실수형으로 만들기
arr = np.array([1, 2, 3, 4, 5], dtype=np.float64)
print(arr) # [1. 2. 3. 4. 5.]기초 함수들
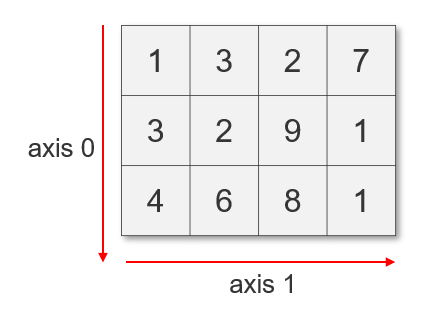
: 주의할 점: 축은 0부터 시작한다는거~!
-
np.ndim(): rank(차원. 축의 개수) -
np.shape(): 축의 길이, 모양을 반환 # (3, )- 예: a.shape # (2, 3, 3) 해석은?
: 뒤에서부터 읽자! 3 x 3짜리 분석 단위가 2개 있다. (3행 3열짜리 분석단귀가 2개 있다)
- 예: a.shape # (2, 3, 3) 해석은?
-
np.dtype(): 데이터 형식 # int32텍스트 -
a.reshape(x, y)또는np.reshape(a, (x, y)): 다시 shape 해줘. 즉 배열의 요소가 사라지지 않는다면(요소 개수가 변하지 않는다면) 형태를 변화시킴- -1을 입력하면, 나머지 축에 맞추고 -1로 쓴 축은 네가 알아서 바꿔줘~ 란 뜻!
- ndarray 가 아닌 경우, 먼저 np.array()로 ndarray로 바꾼후 reshape 하기.
: 만약 다시 list로 바꾸고 싶다면tolist()
-
np.zeros(): 배열의 모든 요소를 0으로 채워라 # np.zero((2, 2)) -
np.ones(): 배열의 모든 요소를 1로 채워라 -
np.full(): 배열의 모든 요소를 특정 값으로 채워라- # np.full((2, 2), 7.) # array([[7., 7.], [7., 7.]])
-
np.eye(): 정방향 행렬로 만들어라 -
np.random.random(): 랜덤 값으로 채워라 -
np.inf: infinity 무한 -
np.nan: not a number 정의할 수 없는 숫자
np.array([1, np.inf, np.nan]) # array([ 1., inf, nan])
np.multiply(a, 3) # array([ 3., inf, nan])배열 인덱싱과 슬라이싱
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])1. x번째 행, y번째 열의 요소 조회
# 두 번째 행 두 번째 열의 요소 조회
a[1, 1] # 스칼라 값 출력: # 5
a[[1], [1]] # 목록으로 집어넣어서 출력하니, 1차원 값으로 나옴: # [5]# 불리안 방식 배열 인덱싱(조건으로 조회하기)
a[0][a[0] >= 2] # 1차원 출력: [2 3]2. x_1번째 행, y_1번째 열과 x_2번째 행, y_2번째 열의 요소 조회
# 첫 번째 행 첫 번째 열, 두 번째 행 두 번째 열의 요소 조회
# (0, 0)과 (1, 1) 데이터 두개를 가져옴
a[[0, 1], [0, 1]] # 출력: [1 5]
# 입력
a[0:2, 0:2]
# 2차원으로 출력됨
[[1 2]
[4 5]]3. 출력이 1차원, 2차원일때 비교
# 1차원으로 출력됨 # 출력: [7 8 9]
a[2] # y(열)의 경우 생략 가능. 그러나 x(행)은 생략 불가능!!
a[2, :]
a[2, [0, 1, 2]]
a[[2], [0, 1, 2]] # 왜 얘는 1차원 출력일까?!?!?!? 체크!
# 2차원으로 출력됨 # 출력: [[7 8 9]]
a[[2]]
a[[2], :]
a[2:3, 0:3] # x, y 모두 슬라이싱 사용하면, 2차원으로 출력됨4. 팬시 인덱싱(fancy indexing) ?
a = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
idx = np.array([True, False, True, False, True,
False, True, False, True, False])
a[idx] # array([0, 2, 4, 6, 8])- 배열 인덱스의 크기가 원래의 배열 크기와 달라도 상관없다.
: 같은 원소를 반복해서 가리키는 경우에는 배열 인덱스가 원래의 배열보다 더 커지거나 작아지기도 한다.
a = np.array([11, 22, 33, 44, 55, 66, 77, 88, 99])
idx = np.array([0, 0, 0, 1, 1, 2])
array([11, 11, 11, 22, 22, 33])* 에러가 나는 경우
# invalid syntax
a[2, [:]]
a[[2], [:]] 배열 연산과 집계
기초적인 연산
-
np.add()or+ -
np.subtract()or- -
np.multiply()or*- 일반적인 list * 정수
: 객체의 크기가 정수배 만큼으로 증가. 원소 각각을 곱하려면 for문 사용 - 벡터화 연산
: 비교 연산과 논리 연산을 포함한 모든 종류의 수학 연산에 대해 적용
a = [1, 2, 3] b = np.array([1, 2, 3]) print(a * 3) # [1, 2, 3, 1, 2, 3, 1, 2, 3] print(b * 3) or print(np.multiply(b, 3)) # [3 6 9] - 일반적인 list * 정수
-
np.divide()or/ -
np.power()or**: 제곱 -
np.sqrtor배열 ** (1/2): 제곱근
집계 함수
np.sum(),np.mean(),np.std()np.argmax(),np.argmin(): 최댓값/최솟값의 첫번째 인덱스axis = 0: 행 방향으로 집계해라axis = 1: 열 방향으로 집계해라- 예: np.sum(a, axis = 1): 열 방향, 즉 각 행마다 더하라
np.where(조건문, 참일 때 값, 거짓일 때 값)np.linspace(시작값, 끝값, 사이 값 갯수): 끝값을 포함함. 실수형 가능.- 비교: range(시작값, 끝값, 간격): 끝값은 포함하지 않음. 정수만 가능.
