- 출처
- 핸즈온 머신러닝2
- 핸즈온 머신러닝2 github
- 핸즈온 머신러닝2 6장 pdf
- 핸즈온 머신러닝2 6장 강의
- 되도록이면 책의 내용과 코드를 그대로 옮기기 보다는 요약과 보충설명!
읽기전에
개념 정리
python 정리
6장 결정 트리(decision tree)
특징 및 장점
- 분류, 회귀, 다중출력도 가능한 만능 알고리즘!
- 랜덤 포레스트의 기본 구성 요소
- 불순도 계산 시에 샘플 특성값을 사용하지 않음. 즉 거리 개념이 들어가지 않기 때문에 데이터 전처리가 거의 필요하지 않음
- 각 특성이 개별 처리되기 때문에 데이터 스케일에 영향을 받지 않아 특성의 정규화나 표준화가 필요없다.
- 시각화로 한눈에 모델을 볼 수 있음
화이트 박스 모델이다
: 직관적, 결정 방식을 이해하기 쉬움
- 반대로, 블랙 박스 모델이란?
: 랜덤 포레스트, 신경망 등.
: 성능이 뛰어나고 예측을 만드는 연산 과정을 쉽게 확인할 수 있지만, 예측이 나온 과정을 설명하기 어려움.
클래스 확률 추정
- 한 샘플이 특정 클래스에 속할 확률 추정 가능
단점
- 모든 분할은 축에 수직이기 때문에 계단 모양의 결정 경계를 만듦
: 훈련 세트의 회전에 민감 - 훈련 데이터의 작은 변화에도 매우 민감
- 과대적합 가능성
결정 트리 학습과 시각화
- 분류
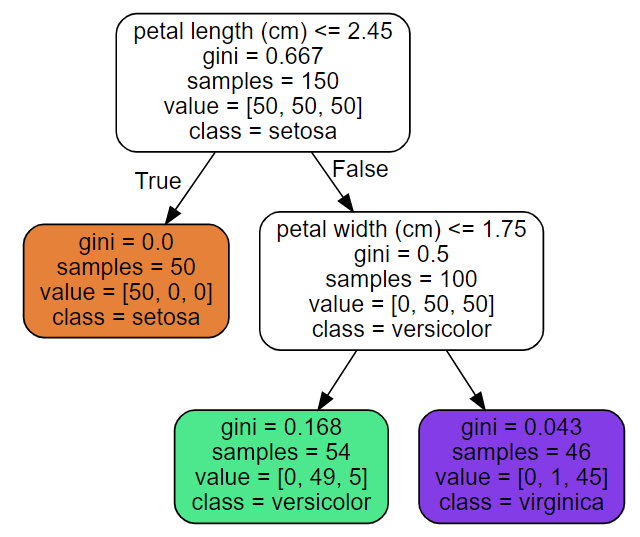
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)- 루트 노드: 깊이가 0인 맨 꼭대기 노드
- 리프 노드: 자식 노드를 가지지 않는 노드
- 자식 노드
- 두 개씩 가지를 뻗으며 성장: True of False
- 순수 노드(퓨어 노드): 한 노드에 한 클래스만 담김. gini=0
max_depth=2: 깊이 설정. 만약 설정 안하면, 리프노트가 순수해질 때까지 진행. 즉 과대적합 된다.plot_tree(): 트리 그리기
CART 훈련 알고리즘
- 훈련 세트를 두개의 서브셋으로 나누기를 반복. 최대 깊이 혹은 불순도를 줄이는 분할을 찾을 수 없을 때 멈춤.
- 탐욕적 알고리즘(그리디)
: 각 깊이에서 최적의 분할을 찾음
: 항상 최적해를 보장하지는 않는다.
계산 복잡도
- 예측의 복잡도:
- 훈련 복잡도: : 훈련 세트가 클 경우, 많이 느림
불순도
- 기본적으로는 지니 불순도,
criterion="entropy"로 하면 엔트로피 불순도 가능 - 지니 불순도와 엔트로피 불순도의 차이는 크게 없지만, 지니 불순도가 조금 더 빠름.
- 그러나 엔트로피가 조금 더 균형 잡힌 트리를 만듦.
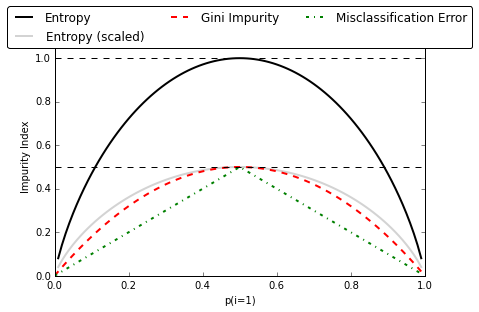
- 출처: https://tensorflow.blog/2018/03/25/결정-트리와-불순도에-대한-궁금증/
지니 불순도
gini=0: 한 노드의 모든 샘플이 같은 클래스에 속해있을 떄. 즉 순수 노드- 두개로 나눌때, 지니 불순도의 최댓값은 0.5
엔트로피 불순도
- 모든 메시지가 동일할 때, 즉 어떤 세트가 한 클래스의 샘플만 담고 있을 때 엔트로피는 0이 됨
- 최댓값은 1
- 지니 불순도에서는 제곱이었다면, 엔트로피 불순도에서는 log로
규제 매개변수
- 훈련 데이터에 대한 제약이 거의 없지만, 제한을 두지 않으면 과대적합되기 쉬움.
- 비파라미터 모델임
: 훈련되기 전에 파라미터 수가 결정되지 않음. 그래서 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유로움.- 그럼, 파라미터 모델이란?
: 선형 모델 등
: 얘는 과소적합 될 가능성이 높음.
- 그럼, 파라미터 모델이란?
- 흔히
max_depth규제 min_samples_split,min_samples_leaf,min_weight_fraction_leaf,max_leaf_nodes,max_features규제
과대적합 제어
- 사전 가지치기(pre-pruning) : 노드 생성을 미리 중단
- 사후 가지치기(pruning) : 트리를 만든후에 크기가 작은 노드를 삭제
- 트리의 최대깉이나 리프 노드의 최대 개수를 제어
- 노드가 분할 하기 위한 데이터 포인트의 최소 개수를 지정
- 출처: https://codingstudyroom.tistory.com/entry/머신러닝-Decision-Tree결정트리-스마트인재개발원
회귀
- 각 노드에서 클래스를 예측(분류에서)하는 대신 어떤 값을 예측.
- MSE를 최소화하도록 분할 반복
- 결정 트리 회귀 모델을 그래프로 나타냈을 때, 각 영역의 예측값은 항상 그 영역에 있는 타깃값의 평균이 된다(즉, 리프 노드에 있는 샘플의 평균값)
궁금증
- 237p. '지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지로 고립시키는 경향이 있는 반면, 엔트로피가 조금 더 균형 잡힌 트리를 만든다'의 의미와 이유?
- 데이터의 회전은 무엇을 의미하나? 데이터의 변형을 초래하는건 아닌가?
