- 출처
- 되도록이면 책의 내용과 코드를 그대로 옮기기 보다는 요약과 보충설명!
읽기전에
개념 정리
python 정리
7장 앙상블 학습과 랜덤 포레스트
- 앙상블: 여러 개의 예측기로 이루어진 그룹
- 앙상블 학습: 예측기 여러 개의 결과를 종합하여 예측값을 지정하는 학습
- 앙상블 기법: 앙상블 학습을 지원하는 앙상블 학습 알고리즘
투표 기반 분류기
직접 투표(hard voting) 분류기
- 분류기를 여러개 훈련 시킨 후에, 각 분류기의 예측을 모아서 가장 많이 선택된(가장 많은 투표를 받은) 클래스를 예측. 즉 다수결 투표
- Why?
: 큰 수의 법칙 - hard voting시 동점이면? 오름차순 선택
- classifier 1 -> class 2
classifier 2 -> class 1
the class label 1 will be assigned to the sample.
- classifier 1 -> class 2
제한점
- 모든 분류기가 완벽하게 독립적일것
- 오차에 상관관계가 없을 것
- 제한점 극복하기 위해서: 각기 다른 알고리즘으로 학습시키면, 앙상블 정확도가 높아짐
python
- 사이킷런
VotingCalssifier
간접 투표(soft voting) 분류기
- 개별 분류기의 예측을 평균 내어 확률이 가장 높은 클래스를 예측.
- 직접 투표 방식보다 성능이 더 높음
python
- 사이킷런
VotingCalssifier에서voting="soft"
bagging, pasting
- 같은 알고리즘을 사용하되 훈련 세트의 서브셋을 무작위로 구성하여 분류기를 각기 다르게 학습시키는 방법
- 훈련 세트에서 중복을 허용하여 샘플링(복원 추출)하면 bagging(bootstrap aggregating)
- 훈련 세트에서 중복을 허용하지 않고 샘플링(비복원 추출) 하면 pasting
- 모든 예측기가 훈련을 끝낸 후, 이들의 예측을 모아서 새로운 샘플에 대한 예측을 만듦
- 분류: 통계적 최빈값(직접 투표처럼)
- 회귀: 평균값
특징
- 개별 예측기보다 편향은 비슷, 분산은 줄어듬
- 즉 훈련 세트의 오차 수는 비슷, 결정 경계는 덜 불규칙
- 편향: bagging > pasting
- 분산: bagging < pasting
- 전반적으로 bagging이 더 선호됨
- 분산이 클 때, bagging 사용? 근데 결국 둘다 써봐야할듯
python
- 사이킷런
BaggingClassifier또는BaggingRegressor - pasting은
bootstrap=False지정 - 만약
BaggingClassifier에서 개별 분류기의 클래스 확률을 추정 가능하면, 간접 투표 방식을 사용
oob(out-of-bag) 샘플 평가
: bagging시, 샘플링 되지 않은 37%의 훈련 샘플
- 이 oob를 검증 세트로 활용
BaggingClassifier에서oob_score=True
feature sampling 종류
- 랜덤 패치: 훈련 특성과 샘플을 모두 샘플링. 즉 행과 열 모두 샘플링
- 랜덤 서브스페이스: 훈련 특성은 샘플링(
bootstrap=False,max_samples=1.0), 훈련 샘플은 모두 사용(bootstrap_features=Trueand/ormax_features는 1.0보다 작게 설정). 즉 열은 샘플링, 행은 모두 사용.
random forest
- 트리 노드 분할 시, 무작위로 선택한 특성 후보 중에서 최적의 특성을 다시 찾는 식으로 무작위성을 주입함.
- 편향은 늘어나지만, 분산은 낮추어서 모델 성능이 좋아짐.
n_estimators,max_leaf_nodes
extra tree(extremely randomized trees) 앙상블
= 극단적으로 무작위한 트리의 랜덤 포레스트
- 편향은 늘어나지만, 분산은 낮추어서 모델 성능이 좋아짐.
- 트리 분할 시 무작위 분할 후 최상의 분할을 선택하기 때문에 트리가 더욱 무작위하게 분할됨
ExtraTreesClassifier,ExtraTreesRegressor
feature importance 특성 중요도, 변수 중요도
- decision tree 기반 모델은 모두 feature importance를 제공
- 평균(가중치 평균)적으로 불순도를 얼마나 감소시키는가?
feature_importance_
boosting(hypothesis boosting)
- 약한 학습기를 여러 개 연결하여 강한 학습기를 만드는 앙상블 방법
AdaBoost(에이다부스트)
- 이전 모델이 과소적합했던 훈련 샘플의 가중치를 더 높힘.
- 학습, 예측 -> 이전에 잘못 분류된 훈련 샘플의 가중치를 높힘 -> 다시 훈련, 예측 -> 반복...
- 경사 하강법과 비슷한 측면이 존재
- 병렬화(분할)이 불가능하기 때문에, 배깅이나 페이스팅 만큼 확장성이 높지 않음
AdaBoostClassifier,AdaBoostRegressor
gradient boosting
- 이전 모델의 예측의 잔여 오차에 새로운 예측기를 학습 시킴
- 회귀: GBRT(gradient boosted regression tree), 분류
GradientBoostingRegressor,
learnig_rateparameter: 각 트리의 기여 정도를 조절n_estimators- 확률적 그레이디언트 부스팅
XGBoost(extreme gradient boosting)
stacking
- "앙상블에 속한 모든 예측기의 예측을 취합하는 간단한 함수를 사용하는 대신, 취합하는 모델을 훈련시킬 수 없을까?"
- blender(meta learner)
: cross-validation 기반
간단하고 쉽게 한번 살펴보자. CV fold는 3으로 고정하였고, test set은 별도로 존재하는 것으로 가정한다.
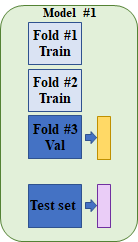
그림 1과 같이, 한 모델이 있다. train fold를 이용하여 1번 모델을 훈련하고, validation fold를 이용하여 모델 예측 값을 계산해 낸다.
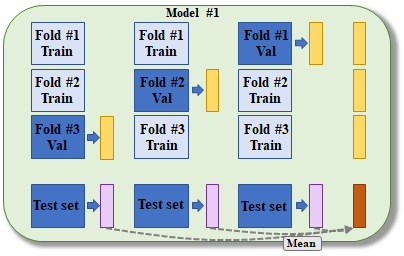
그림 2와 같이 각 valdiation fold 마다 예측 값을 계산하여 이를 concatenate 시키고, test set을 이용한 예측 값 3개(그림 2의 보라색 박스)는 평균을 내어 meta 모델에 사용되는 test set으로 만든다. 그림에서 정렬된 3개의 노란 박스는 결국 한 모델에서 계산되어진, 모든 샘플에 대한 예측 값들이 된다.
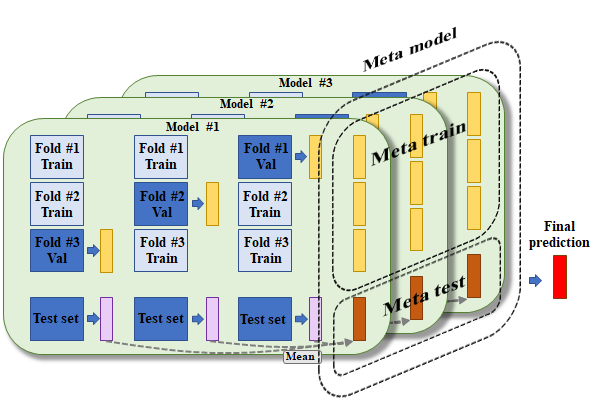
여기까지의 과정을 다수의 모델에 대해서 반복하고, 그 출력 값들을 concatenate 하게 되면 결국 meta train 데이터와 meta test data를 얻게 된다. 그림에서 보는 것과 같이, meta train 데이터의 dimension은 test set을 제외한 총 샘플수 x 모델 갯수가 될 것이고, meta test 데이터의 dimension은 test set의 샘플 수 x 모델 갯수가 될 것이다. 이를 통해 meta 모델이라고 불리는 2차 모델이 훈련 및 최종 예측 값 출력을 하게 되는 것이다.
다소 복잡한 과정이라 생각될 수 있지만, 그림을 통해서 찬찬히 살펴보면 크게 어려운 개념이 아니다.
궁금증
- "xgboost에서 learning_rate와 n_estimators는 상호보완적인 조합 관계이며,learning_rate를 낮추고 n_estimators를 높히면 성능이 높아지지만, 시간이 오래 걸리고 과적합의 위험이 있다. 그 반대의 경우는 과소적합의 위험이 있다" 라고 이해하였습니다. 이때 만약 n_estimators는 고정 시킨 채 learning_rate만 조정한다면, 성능에는 영향이 없고 소요 시간의 차이만 발생하는걸까요?
- learning_rate을 낮추고 n_estimators 이면 성능이 좋아진다고 일반화 시킬 수는 없습니다. 데이터 상황에 맞게 실험해봐야 합니다.
n_estimators 를 고정하고 learning_rate를 조절하면 성능에 차이가 납니다.^^
