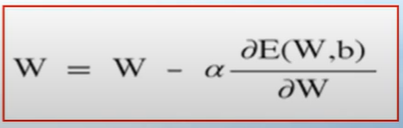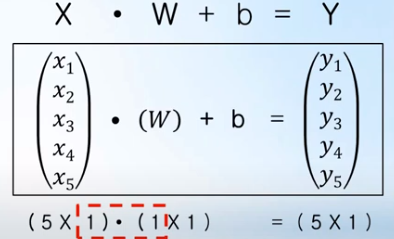머신러닝 12 ~ 18

머신러닝:

• 데이터를 이용하여 데이터 특성과 패턴을 학습하여, 그 결과를 바탕으로 미지의 데이터에 대한 그것의 미래 결과(값, 분포)를 예측
• 지도학습과 비지도 학습으로 나뉨

지도학습:

• 입력 값과 정답을 포함하는 Training Data를 이용하여 학습하고, 그 학습된 결과를 바탕으로 미지의 데이터(Test Data)에 대해 미래 값을 예측하는 방법
• 어떤 종류의 미래 값을 예측하냐에 따라, 회귀(Regression)과 분류(Classification)으로 나뉨

회귀:

• Training Data를 이용하여 연속적인 (숫자) 값을 예측
  공부시간과 시험성적 등의 관계

분류:

• Training Data를 이용하여 주어진 입력값이 어떤 종류의 값인지 구별
  공부시간과 합격당락의 관계

비지도학습:

• 학습할 데이터의 정답은 없고, 입력만 있음, 입력데이터의 패턴/특성 등을 학습을 통해 발견하는 방법
• 입력값 자체의 특성과 분포만을 확인해서 그룹화하는 군집화(Clustering)이 있음

Linear Regression:

• 학습(Learning):
  training data의 특성을 가장 잘 표현할 수 있는 가중치 W(기울기), bias b(y절편)을 찾는 것

• 오차(error):
  traning data의 정답(t)와 직선 y = Wx+b 값의 차이
  error = t - y = t - (Wx+b)
  => 머신러닝의 regression 시스템은, 모든 데이터의 error의 합이 최소가 돼서, 미래 값을 잘 예측할 수 있는 W와 b 값을 찾아야 함

• 손실함수(loss function):
  training data의 정답(t)과 입력(x)에 대한 계산 값 y의 차이를 모두 더해 수식으로 나타낸 것
  오차(t-y)를 통해 손실함수를 구하면 오차 합이 0이 나올 수도 있어, 최소 오차 값인지 판별이 어려움
  => 손실함수에서 오차를 계산할 때는 (t-y)^2 를 사용
  
  손실함수는 모든 데이터에 대한 평균 오차값을 나타냄
  training data를 바탕으로 손실 함수 E(W, b)가 최소값을 갖도록 (W, b)를 구하는 것이 regression model의 최종 목적

• 경사하강법(gradient decent algorithm):
  W에서의 직선의 기울기인 미분 값을 이용하여, 그 값이 작아지는 방향으로 진행하여 손실함수 최소값을 찾는 방법

1. 임의의 가중치 W 선택
2. 그 W에서의 직선의 기울기를 나타내는 미분 값 을 구함
3. 그 미분 값이 작아지는 방향으로 W 감소 시켜 나감
4. 최종적으로 기울기가 더 이상 작아지지 않는 곳을 찾을 수 있는데, 그곳이 손실함수 E(W) 최소값임을 알 수 있음
   
   편미분 값이 양수이면 그 값만큼 빼서 W를 이동 / 음수이면 그 값만큼 더해서 W를 이동 하여
   W를 찾기
   => 이러한 편미분으로 W와 b를 구하여 최적의 손실함수를 구하는 것이 linear regression의 목표

• 오차 계산 예제:
  오차를 계산하기 위해서는 training data의 모든 입력 x에 대해 각각의 y=Wx+b 계산을 해야 함
  => 이때 입력 x, 정답 t, 가중치 W 모두를 행렬로 나타낸 후에, 행렬 곱(dot)을 이용하면 계산 값 y 또한 행렬로 표시되어 모든 입력 데이터에 대해 한번에 쉽게 계산 가능

Logistic Regression
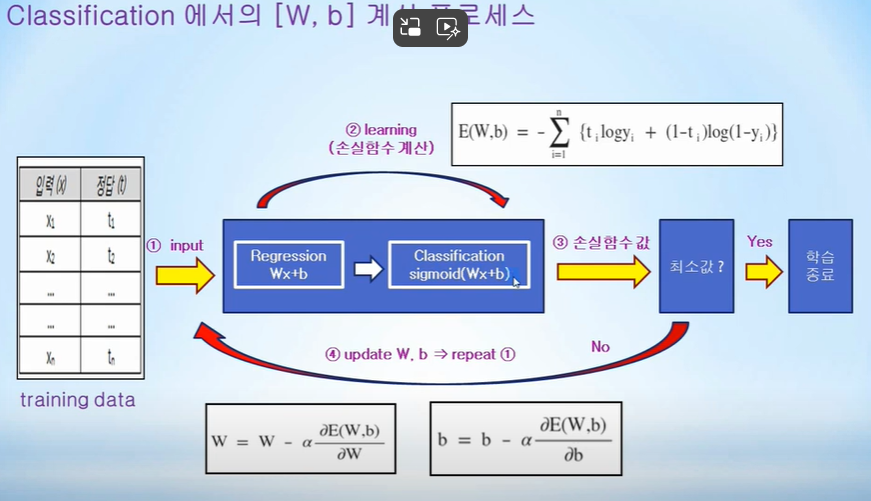
=> Classification: Training Data 특성과 관계 등을 파악 한 후에, 미지의 입력 데이터에 대해서 결과가 어떤 종류의 값으로 분류 될 수 있는지를 예측하는 것

• Logistic Regression 알고리즘:

1. Training Data 특성과 분포를 나타내는 최적의 직선을 찾고(Linear Regression)
2. 그 직선을 기준으로 데이터를 위 또는 아래 등으로 분류(Classification) 해주는 알고리즘
   => 출력 값 y 가 1 또는 0 만을 가져야만 하는 Classification에서,
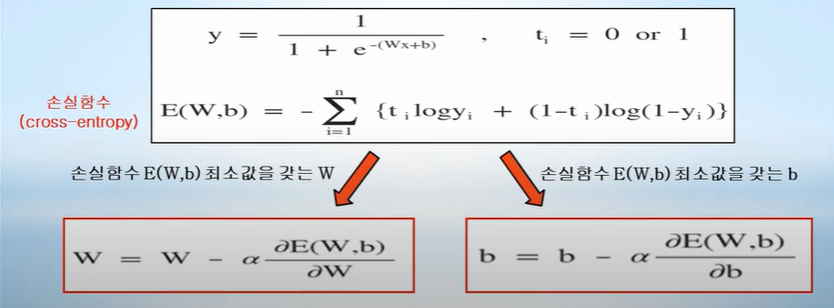
   함수 값으로 0~1 사이의 값을 가지는 sigmoid 함수를 사용하여 Classification을 구축 가능
   => sigmoid 계산 값이 0.5보다 크면 결과로 1이 나올 확률이 높다는 것이기 때문에 출력 값 y를 1로 정의 / 0.5 미만이면 결과롤 0이 나올 확률이 높다는 것이므로 출력 값 y를 0으로 정의

• 손실함수(cross-entropy)
  

• Classification
  
  => Regression 과 sigmoid를 통한 Classification으로 손실함수 cross-entropy를 계산하여 최소값을 찾는다(W, b를 지속적으로 업데이트 하며)

논리게이트:

• AND, OR, NAND, XOR 논리테이블은 입력데이터, 정답데이터인 머신러닝 Training Data와 개념적으로 동일
  => 논리게이트는 손실함수로 cross-entropy를 이용해서 Logistic Regression(Classification) 알고리즘으로 데이터를 분류하고 결과를 예측할 수 있음

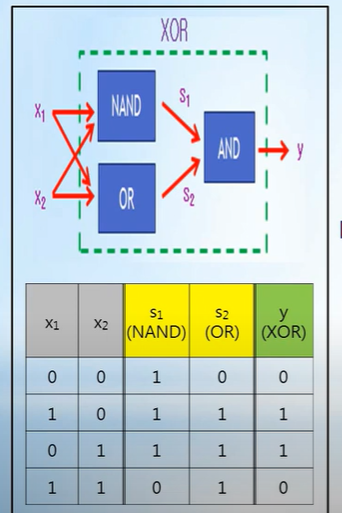
• XOR 게이트는 Logistic Regression으로 분류 불가
  => XOR 내부를 NAND OR, AND 의 조합인 Multi-Layer로 해결 가능
  
  => 각각의 Gate(NAND, OR, AND)는 Logistic Regression 시스템으로 구성됨
  => 이전 Gate의 모든 출력은 다음 Gate의 입력으로 들어감
  => Neural Network(신경망) 기반의 딥러닝 핵심 아이디어