머신러닝 01 ~ 11

인공지능 -> 머신러닝 -> 딥러닝

머신러닝:

• 데이터를 이용하여 명확하게 정의되지 않은 패턴을 학습하고,
  그러한 학습을 바탕으로 미래 결과(값, 분포)를 예측
  ex) Neural Network(NN)

딥러닝:

• 머신러닝의 한 분야로서, 신경망(Neural Network)을 통하여 학습하는 알고리즘의 집합
  ex) CNN, RNN 등

머신러닝
1. Regression(회귀):

• 연속적인 데이터를 학습하여, 이 학습된 결과를 바탕으로 미래에 임의의 데이터가 올 경우에 이 값을 예측하는 것

2. Classification(분류):

• 데이터의 분포를 학습하고, 이 학습된 결과를 바탕으로 미래에 임의의 데이터가 올 경우에 이 데이터가 어느 분포에 속할 지 알려주는 것

딥러닝:
머신러닝의 Neural Network를 구현한 것

• input의 입력을 적당한 가중치를 곱해 모두 더함,
  이 더한 값이 특정 임계값(threshold)를 넘으면 다음 Neural Network로 전달하고 그렇지 않으면 전달하지 않음

머신러닝 프레임워크:

• 머신러닝 알고리즘을 API로 추상화 함으로서 개발을 쉽고 빠르게 할 수 있지만,
  동작원리와 내부 구현을 자세히 알 수 없는 Black Box로서 동작함

파이썬으로 직접 구현:

• 머신러닝 동작원리를 자세히 알 수 있음
  알고리즘에 대한 깊은 이해 가능
  새로운 머신러닝 알고리즘에 대한 빠른 insight 획득 가능

머신러닝과 딥러닝의 데이터는 대다수가 행렬로 표시됨 -> 행렬 연산 숙지 필요

numpy Library

1. vector / martrix 생성
2. 행렵 곱(dot product)
3. broadcast
4. index / slice / iterator
5. concatenate
6. useful function (loadtxt(), rand(), argmax(), )

numpy:

• 머신러닝 코드 개발을 할 때 자주 사용되는 벡터, 행렬 등을
  표현하고 연산할 때 반드시 필요한 라이브러리

• 머신러닝에서 숫자, 사람, 동물 등의 인식을 하기 위해서는 이미지 데이터를 행렬로 변환하는 것이 중요함
  => 행렬을 나타내기 위해서는 리스트를 사용할 수도 있지만, 행렬 연산이 직관적이지 않고 오류 가능성이 높기 때문에, 행렬 연산을 위해서는 numpy 사용이 필수임

vector / martrix

• vector 생성:

1. vector는 np.array( [] )를 사용하여 생성함
2. 머신러닝 코드 구현 시, 연산을 위해서 vector, matrix 등의 형상(shape), 차원(dimension)을 확인하는 것이 필요함
3. 형상 확인 -> .shape 메소드
4. 차원 확인 -> .ndim 메소드
5. vector 간 산술연산(+, -, X, /) 은 벡터의 각각의 원소에 대해서 행해짐

• martirx(행렬) 생성:
  np.array( [], [], ) 를 사용하여 생성
  ex) A = np.array([ [1, 2, 3], [4, 5, 6 ] ])

• 형 변환 (reshape)
  vector를 matrix로 변경하거나 matrix를 다른 형상의 matrix로 변경하기 위해서 reshape()을 사용하여 행렬의 shape을 변경하여야 함

행렬 곱

• A 행렬과 B 행렬의 행렬 곱은 np.dot(A, B) 순서로 나타내며, 행렬 A의 열 벡터와 B 행렬의 행 벡터가 같아야 함.
  만약 같지 않다면 reshape 또는 전치행렬(transpose) 등을 사용하여 형 변환을 한 후에 행렬 곱을 실행해야 함

• 행렬 곱은, 행렬의 원소 개수가 같아야만 계산할 수 있는 사칙연사의 한계가 있다.
  이 한계를 극복하기 위해

1. 행렬곱 조건을 만족하는 다양한 크기의 행렬을 연속으로 만들고
2. 행렬 곱을 연속으로 계산하면서
3. 결과값을 만들 수 있기 때문에 머신러닝과 이미지 프로세싱 분야에서 자주 사용됨
   ex) 입력 값 (64 X 64) X 특성값 (64 X 256) * (256 X 10) = 결과값 (64 X 10)
   행렬 곱을 사용하지 않고 산술연산만 가능하다면, 입력 행렬의 크기를 가지는 특성 값만을 사용해야 하여 다양한 특성을 갖는 필터 개발이 불가능함

broadcast

• numpy에서는 크기가 다른 두 행렬 간에도 사칙연산을 할 수 있는데, 이를 broadcast라 함
  => 차원이 작은 쪽이 큰 쪽의 행 단위로 반복적으로 크기를 맞춘 후에 계산
  ex) C = np.array([ [1, 2], [3, 4] ]) , D = np.array([4, 5]), print(C+D)
  이때, [4,5]를 ([ [4, 5], [4, 5] ])로 broadcast 하여 연산이 가능해짐

• 이러한 broadcast는 행렬곱 연산에는 적용되지 않고, 사칙연산에만 적용됨!

transpose(전치행렬)

• 원본 행렬의 열은 행으로, 행은 열로 바꾼 것
  원본 행렬이 A라 하면, 전치 행렬은 AT(T는 위첨자)로 나타냄
• B = A.T 로 표현 (.T 연산자)
• vector는 열, 행이 따로 없어 전치 행렬 적용 안됨, reshape으로 행렬로 만든 후 전치행렬로 만들어야 함

행렬 indexing / slicing

• 리스트에서처럼 인덱싱 / 슬라이싱이 모두 가능

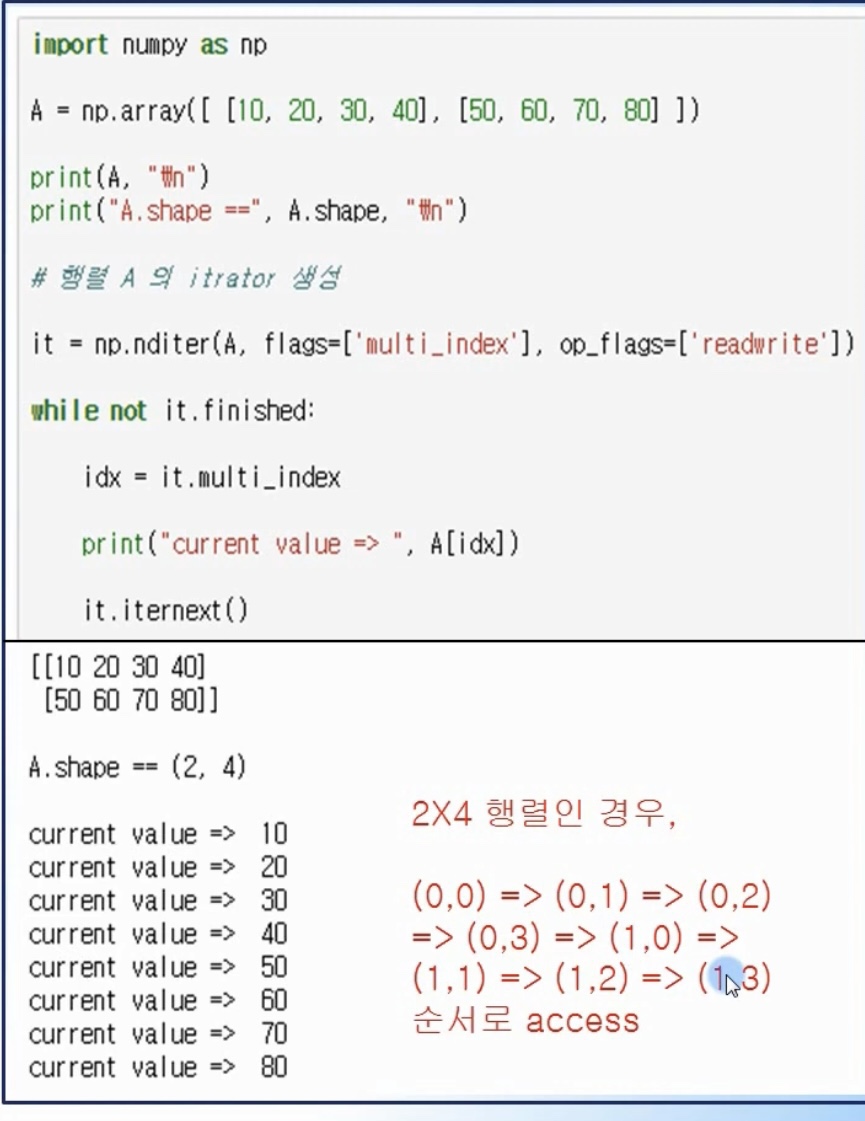
iterator

• 행렬의 모든 원소를 access 하는 경우에는 iterator 사용이 효율적
• 원소의 값을 순차적으로 획득할 수 있음
  (행 단위로 접근하여, 처음부터 마지막 원소 모두를 가져올 수 있음)
  

numpy.concatenate:

• 기존 행렬에 행 또는 열 추가하기 위해 사용
  => 머신러닝의 regression(회귀) 코드 구현 시 weight(가중치)와 bias(바이어스)를 별도로 구분하지 않고 하나의 행렬로 취급하기 위함

• ex)
  row_add = np.array([70, 80, 90]).reshape(1,3) #기존 행렬과 행,열 일치시키기
  column_add=np.array([1000, 2000]).reshape(2,1)
  B = np.concatenate((A, row_add), axis=0) #axis=0 => 행(row) 기준
  C = np.concatenate((A, column_add), axis=1) #axis=1 => 열(column) 기준

numpy.loadtext:

• seperator로 구분된 파일에서 데이터를 읽기 위한 함수
  => 데이터에서 리턴값은 행렬이기 때문에 인덱싱 또는 슬라이싱을 이용하여 데이터를 분리 할 필요가 있음
  => 머신러닝 코드에서 입력데이터와 출력데이터를 분리하기 위함

numpy.random.rand:

• 0과 1사이의 임의의 실수값을 랜덤하게 벡터 또는 행렬 형태로 리턴해줌
  => 가중치나 바이어스 등을 임의로 설정할 때 자주 사용

numpy.sum / exp / log:

• 합 / 곱 / log 값을 구해주는 함수

numpy.max / min / argmax / argmin:

• 최대, 최소, 최대값의 인덱스, 최소값의 인덱스 리턴
  행렬에서는, 행 기준으로 찾고 싶을 때는 axis = 1으로 열 기준으로는 axios = 0으로 사용
  => classfication(분류)에서 정답의 위치를 찾을 때 사용

numpy.ones / zeros:

• ones: 주어진 행렬의 형상을 모두 1로 채움
  zeros: 주어진 행렬의 형상을 모두 0으로 채움
  ex)
  A = np.ones([3, 3]) -> [[1,1,1], [1,1,1], [1,1,1]]

matplotlib, scatter plot

• 실무에서는 머신러닝 코드를 구현하기 전에,
  입력 데이터의 분포와 모양을 먼저 그래프로 그려보고, 데이터의 특성과 분포를 파악한 후 어떤 알고리즘을 적용할 지 결정하고 있음
  =>
  matplotlib: 데이터 시각화를 위해 사용하는 라이브러리
  line plot, scatter plot: 데이터의 분포와 형태를 파악

수치미분

• 미분, 편미분, 체인룰: 머신러닝에서 사용되는 1차 함수의 기울기와, y절편을 계산하고 이러한 것들을 최적화 시키기 위해 반드시 필요

미분

• 입력변수 x가 델타 x만큼 미세하게 변할 때, 함수 f가 얼마나 변하는지 알 수 있는 식을 구해라
  => 함수 f(x)는 입력 x의 미세한 변화에 얼마나 민감하게 반응하는지 알 수 있는 식을 구해라
• 이를 통해 얻을 수 있는 insight
  => 입력 x를 현재 값에서 아주 조금 변화시키면, 함수 f(x)는 얼마나 변하는가?
  => 함수 f(x)는 입력 x의 미세한 변화에 얼마나 민감하게 반응하는가?

편미분

• 변수가 여러개인 함수에 대해 미분을 원하는 변수 하나를 선택하고, 그 하나에 대해 편미분
  => x, y로 구성된 다변수 함수가 있을 때, x 값을 고정한 상태에서 y 값을 미세하게 변화시킬 때, f(x, y)가 얼마나 변화하는지 알아보겠다는 의미

체인룰

• 합성함수를 구성하는 각 함수의 미분의 곱
  => 가중치를 업데이트하고, 오차역전파(backword propagation)에서 중요하게 쓰임