BoostCamp AI Tech 4기 논문 스터디 4회차

Factorization Machines(ICDM'10)

---

Abstract

Support Vector Machines(SVM)의 장점과 factorization models을 결합한 Factorization Machines(FM) 소개

• SVM과 다르게 FM은 factorized parameters를 사용해 변수간 모든 상호작용을 모델링
• SVM이 실패하는, sparsity가 매우 큰 문제에서 상호작용을 추정하는 게 가능
• FM은 선형적인 시간 안에 계산 가능하고, 직접 최적화될 수 있음
• 따라서 비선형의 SVM과 달리 dual form의 변환이 필요 없고, support vector가 없어도 parameter 최적화 가능
• factorization models는 MF, SVD++, PITF, FPMC 등 다양함
  • 이들은 일반적인 예측이 아니라 특정한 input에 대해서만 예측이 가능
  • 게다가 model equation과 optimization algorithm도 각각 개별적으로 유도됨
• FM은 입력 데이터(특징 벡터)를 특정하는 것만으로 다른 factorization models를 모방할 수 있으므로 factorization models에 대해서 전문 지식이 없어도 사용 가능

입력 데이터를 특정한다는 게 무슨 뜻일까?
계속 읽어보자

1. INTRODUCTION

• SVM는 머신러닝과 데이터마이닝에서 가장 인기있는 방법
• 그러나 CF와 같은 세팅에서는 SVM이 중요한 역할을 못하고 아래 모델들이 더 좋은 성능
  • standard matrix, tensor factorization model을 직접 적용한 PARAFAC
  • factorized parameters를 쓰는 특별한 모델들
• SVM은 sparse data에서 신뢰할만한 parameter 학습을 하지 못하기 때문
• 하지만 위의 모델은 standard prediction data에 적합하지 않고, 학습 모델링과 디자인에 개별적인 작업이 필요함
• 그래서 SVM과 같은 새로운 일반적인 예측인 FM을 제시, 이것은 높은 sparsity data에서도 신뢰할만한 parameter 학습 가능
• dense parametrization을 사용하는 SVM과 달리 factorized parametrization을 사용
• FM의 방정식이 선형 시간 안에 계산되고 선형적인 수의 parameter 수에 의존하므로 예측을 위한 training data(SVM의 support vector와 같은 것)의 저장 없이 직접적인 parameter의 최적화 및 저장이 가능
• MF, SVD++, PITF, FPMC 등의 CF 작업에서 FM이 가장 성공적인 접근을 한다는 것을 보여 줌

Advantages
1. FM은 SVM이 실패한 sparsity data 환경에서도 parameter 추정이 가능
2. support vector에 의존하는 SVM과는 달리, FM은 선형적인 복잡성을 가지므로 primal에서 최적화 가능
3. 입력 데이터의 feature vector를 정의하는 것만으로도 최신 models를 모방할 수 있어, 모든 실수값 feature vector에서 작동하는 general predictor로 사용

2. PREDICTION UNDER SPARSITY

• 가장 일반적인 예측이란? $y = \mathbb{R}^n \rightarrow T$를 예측하는 것
  • 실수 값인 feature vector $x \in \mathbb{R}^n$가 속하는 영역으로부터
  • 목표 domain인 $T$를 도출하는 함수 $y$를 예측하는 것
  • 예를 들어, 회귀 문제에서는 목표 domain $T = \mathbb{R}$이고, 분류 문제에서는 $T = \{+, -\}$
• 함수 $y$의 예시로부터 training dataset인 $D = \{(\mathbf{x}^{(1)},y^{(1)}), (\mathbf{x}^{(2)},y^{(2)}), ...\}$를 얻을 수 있음
• 여기서 domain $T = \mathbb{R}$에 대해 함수 $y$가 주어진 $\mathbf{x}$에 값을 매길 수 있으니, 이를 바탕으로 순위 작업 가능
  • 순위 작업 시에 $(\mathbf{x}^{(A)}, \mathbf{x}^{(B)}) \in D$를 사용해 학습
  • 이는 $\mathbf{x}^{(A)}$가 $\mathbf{x}^{(B)}$보다 높은 순위라는 의미
  • 순위 작업은 두 개의 순위가 무조건 결정되니 antisymmetric
• 이 논문에서 다루는 상황은 $\mathbf{x}$가 sparse할 때이고, 웬만한 $\mathbf{x}_i$는 0일 것
• 따라서 $\overline{m}_D \ll n$ 즉, sparsity가 매우 높은 상황임
  • $m(\mathbf{x})$: 0이 아닌 $\mathbf{x}$의 수를 나타내는 함수
  • $\overline{m}_D$: 모든 $\mathbf{x}$에 대한 $m(\mathbf{x})$의 평균

데이터 표현

• notation
  • $u \in U$ 모든 유저 집합 $U$의 원소 개별 유저 $u$
  • $i \in I$ 모든 아이템 집합 $I$의 원소 개별 아이템 $i$
  • $t \in \mathbb{R}$ 실수값으로 표현 가능한 특정 시간 $t$
  • $r \in \{1, 2, 3, 4, 5\}$ 유저가 아이템에 대해 1부터 5까지의 정수로 표현한 점수 $r$
• 이로부터 관측되는 데이터 $S$는 $\{(장원준, 타이타닉, 2022-10, 5), ...\}$와 같이 표현됨
• 이런 데이터를 예측에 사용하여 $y$에 근접한 $\hat{y}$를 예측하는 것
• $Figure 1$을 보면 $S$로부터 데이터를 하나씩 뽑아서 $\mathbf{x}^{(n)}$을 만들어 나열

파란색	주황색	노란색	초록색	갈색
active한 user를 binary하게 표현	movie 각각을 binary하게 표현	해당 유저가 평가한 다른 movie 점수를 정규화(합이 1)하여 표현	2009년 1월부터 몇 달이 지났는지	바로 직전에 평가한 영화를 binary하게 표현

• 주의할 점은, 이 논문에서는 위 데이터만 가지고 예시를 들지만 FM은 SVM과 마찬가지로 general predictor이므로 어느 실수값 벡터에서도 사용 가능하다는 것.

3. FACTORIZATION MACHINES (FM)

이제 FM을 알아보자

A. Factorization Machine Model

1) Model equation

• degree 변수 사이 상호작용을 계산할 때 보려는 변수의 개수
• degree = 2라면 2개의 변수 상호작용을 보겠다는 의미이고, 아래와 같은 식
  $\hat{y}(\mathbf{x}) := w_0 + \sum^n_{i=1}w_ix_i + \sum^n_{i=1}\sum^n_{j=i+1}<\mathbf{v}_i, \mathbf{v}_j>x_ix_j \ \ \ \ \ \ \ \ \ \ \cdot\cdot\cdot\cdot \ \ \ (1)$
  • $w_0 \in \mathbb{R}$, global bias를 의미
  • $\mathbf{w} \in \mathbb{R}^n$
  • $\mathbf{V} \in \mathbb{R}^{n \times k}$
  • $<\mathbf{v}_i, \mathbf{v}_j> := \sum^k_{f=1}v_{i,f}\ \cdot v_{j,f} \ \ \ \ \ \ \ \ \ \ \cdot\cdot\cdot\cdot \ \ \ (2)$
• 여기서 $\hat{w}_{i,j}$는 $i$번째 변수와 $j$번째 변수 사이의 상호작용을 의미하는데, 상호작용 자체에 대한 parameter인 $w_{i,j}$를 사용하지 않음. 이는 상호작용을 이루는 두 변수에 집중하겠다는 의미이지, 상호작용 자체에 집중하는 것이 아니라는 의미.
  • 이것은 degree가 높은 고차원의 상호작용 상황에서 sparsity를 띠는 데이터로도 parameter 추정을 가능하게 하는 key point

2) Expressiveness

• $k$가 충분히 클 때 $W = V \cdot V^t$인 $V$가 존재.
• 다시 말해 FM은 어떠한 상호작용을 나타내는 matrix $\mathbf{W}$이든 $k$만 충분히 크다면 표현하는 것이 가능하다는 의미.
• 하지만 데이터가 sparse하면 복잡한 상호작용 matrix $\mathbf{W}$를 추정할 충분한 데이터가 없기 때문에 $k$를 작게 잡게 되는데... » 그러면 $k$를 제한(restricting)하자!

정리하면, $k$는 FM의 상호작용 표현력을 좌우하는데, $k$를 적절하게 제한한다면 데이터가 sparse하더라도 좋은 generalization과 향상된 상호작용 matrix $\mathbf{W}$를 얻을 수 있음

3) Parameter Estimation Under Sparsity

• sparse한 세팅에서는 상호작용을 직접적/독립적으로 추정하기 위한 데이터가 적음
• 하지만 FM은 factorizing을 통해 상호작용의 독립성을 깨버리므로 다른 상호작용 추정이 가능

상호작용을 깨버린다는 것은, 하나의 상호작용을 단서로 삼아 다른 상호작용에 대한 parameter 추정에 도움을 준다는 의미이고, 각 상호작용을 독립적으로 다루던 SVM과의 차이점

• $Figure 1$을 통한 예시
  A, B, C와 각 영화 평가를 보고 유사함을 따져서 어떤 상호작용 W를 다른 상호작용 W로 추정하는 방식 예시임. (논문 참조)

4) Computation

• 이번엔 FM을 계산적 관점에서 살펴 봄
• 위의 $(1)$ 식은 $\mathrm{O(kn^2)}$의 시간이 걸리지만, 이 식을 적절히 재정리하면 선형의 시간으로 감소가 가능
• 이는 상호작용 그 자체 즉, $(i,j)$로 parameter를 잡은 것이 아니고, 각각 따로 보는 것이라서 아래와 같이 식을 변형하는 것이 가능
  
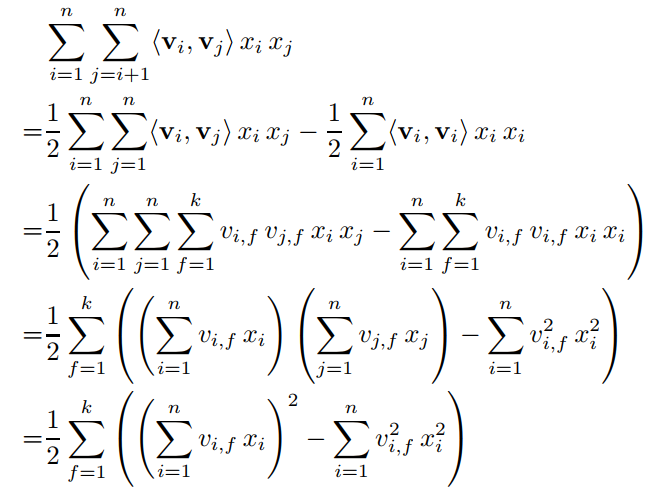
• 위에서부터 한 줄씩 차례로 의미를 설명해 보면 다음과 같음
  • 첫째 줄: 가져온 것이 $(1)$에서 $\mathrm{O(kn^2)}$의 원인이기 때문에 두 변수의 관계를 나타내는 항을 변형하려 함.
  • 둘째 줄: 왜 1/2이 생기지? 모르겟음
  • 셋째 줄: $(2)$의 정의를 가져와서 내적을 풀어서 $\Sigma$로 나타냄
  • 넷째 줄: $j$와 $i$는 독립된 변수라고 했으므로 같은 변수끼리 따로 떼서 곱으로 표현 가능
  • 다섯째 줄: $j$를 $i$로 표현하면 동일한 항이므로 제곱으로 표현 가능
• 이는 $f = 1 \sim k$와 $i = 1 \sim n$으로 표현되는 $\mathrm{O(kn)}$
• 그리고 데이터가 sparse하여 값이 0인 $\mathbf{x}$가 많음 즉, $m(\mathbf{x})$가 낮음
• 따라서 $\overline{m}_D$($m(\mathbf{x})$의 평균적인 값)으로 표현하면 $\mathrm{O(k\overline{m}_D)}$이고, $\overline{m}_D$는 MF에서 일반적으로 2임

B. Factorization Machines as Predictors

• FM은 다양한 예측 작업에 적용 가능
  • 회귀(Regression) $\hat{y}(\mathbf{x})$은 직접적으로 predictor로 사용 가능, 최적화 기준은 $D$에 대한 minimal least square error
  • 분류(Binary classification) $\hat{y}(\mathbf{x})$가 parameter로 사용, hinge loss나 logit loss로 최적화
  • 순위(Ranking) $\mathbf{x}$는 $\hat{y}(\mathbf{x})$ 점수로 줄세우기 되고, 두 벡터의 쌍인 $(\mathbf{x}^{(A)}, \mathbf{x}^{(B)}) \in D$로 pairwise classification loss를 구해 최적화
• 모든 경우에 $L2$ regularization은 overfitting 방지를 위해 사용됨

FM은 관측되지 않은 상호작용을 선형 시간 안에 추정할 수도 있는데, 회귀, 분류, 순위 작업에 적용이 가능하구나

C. Learning Factorization Machines

• FM은 선형적인 시간 안에 계산이 가능하다는 것을 앞에서 증명함
• 이는 FM의 parameter($w_0, \mathbf{w}, \mathbf{V}$)를 학습하는데 Gradient descent가 효율적임을 암시
• $(1)$ 식과 3.A.4에서 변형한 $\hat{y}(\mathbf{x})$식을 각 parameter($w_0, w_i, v_{i,f}$)로 편미분하였을 때 gradient 값은 아래와 같다.

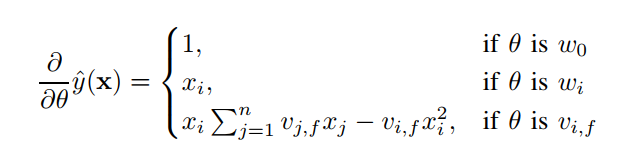
• 각 gradient는 $\mathrm{O(1)}$ 시간 안에 계산 가능
• 각 parameter의 $(\mathbf{x},y)$에 대한 업데이트는 $\mathrm{O(kn)}$ 또는 $\mathrm{O(km(\mathbf{x}))}$ 안에 가능 (선형적인 시간)

D. d-way Factorization Machine

• 계속 설명해 온 것은 2-way FM(degree = 2인 FM, 2개 사이의 상호작용)
• 이를 d-way FM으로 일반화하려 함, d = 2가 아니라 d로 FM 식을 쓰면 아래와 같음
  
• $l$번째 상호작용에 대한 parameter는 아래와 같은 parameter를 가진 PARAFAC 모델에 의해 factorize 됨
  
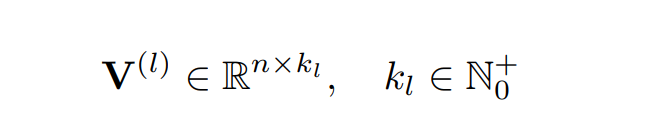
• 위 FM 식 $(5)$는 $\mathrm{O(k_dn^d)}$ 안에 계산이 가능
• 이것도 위에서 했던 방식대로 변형을 거치면 선형적인 시간 안에 해결 가능함

E. summary

• FM은 feature vector 사이에 가능한 모든 상호작용을 모델링
• 이때 factorized 상호작용을 사용하는데, 그 이점은 아래와 같음
  1. 높은 sparsity에도 각 vector 값 사이의 상호작용을 추정할 수 있고, 일반화를 통해 관찰되지 않은 상호작용을 표현할 수 있음(it is possible to generalize to unobserved interactions)
  2. parameter의 수와 시간이 예측과 학습 모두에서 선형적. 이는 SGD를 사용해 직접 최적화가 가능하고 다양한 손실 함수에 대한 최적화를 가능하게 함

4. FMs VS. SVMs

SVM이 못하는 것을 FM이 해결할 수 있는데, FM과 SVM은 어떻게 다를까?

A. SVM model

• 변형된 input $\mathbf{x}$와 model parameter $\mathbf{w}$의 dot product인 $\hat{y}(\mathbf{x}) = <\phi(\mathbf{x}), \mathbf{w}>$로 표현 가능
  • $\phi$: feature space $\mathbb{R}^n$에서 더 복잡한 space인 $\mathcal{F}$로 mapping 하는 함수
  • $\phi$는 kernel과 아래의 관계를 가짐
    

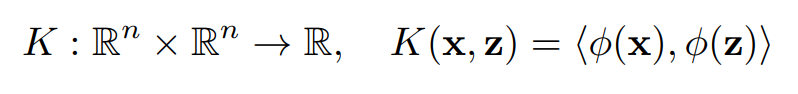
그럼 이제 이러한 kernel에 따라 SVM과 FM이 어떤 관계를 가질지 알아보자

1) Linear kernel

• Linear kernel $K_l(\mathbf{x}, \mathbf{z}) := 1 + <\mathbf{x}, \mathbf{z}>$의 경우 $\phi(\mathbf{x}) := (1, x_1, ..., x_n)$로 mapping하게 됨
• 그럼 linear SVM은 아래와 같은 식으로 쓸 수 있음
  
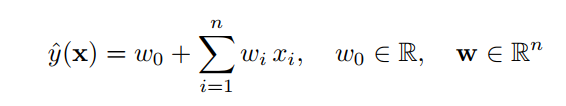
• 이는 d = 1 때의 FM 형태와 동일

2) Polynomial kernel

• Polynomial kernel $K(\mathbf{x}, \mathbf{z}) := (1 + <\mathbf{x}, \mathbf{z}>)^d$의 경우, 만약 d = 2일 때 $\phi(\mathbf{x})$는 아래와 같이 mapping 하게 됨
  
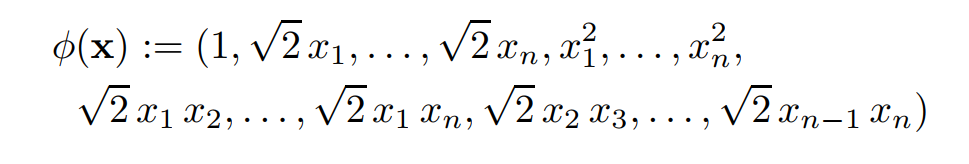
• 그럼 polynomial SVM은 아래와 같은 식으로 쓸 수 있음
  
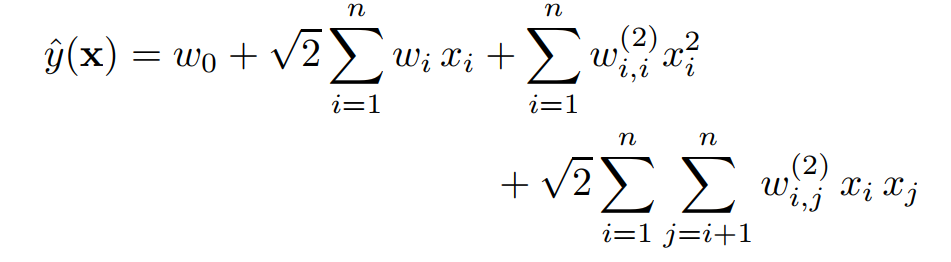
• d = 2 수준까지 상호작용이 표현된다는 점은 앞의 FM 식과 동일
• 차이점은 매개변수화
  • SVM은 $w_{i,j}$가 모두 독립적이라서 $w_{i,j}$와 $w_{i,l}$이 아무런 관계를 맺지 않음
  • FM은 factorization을 통해 $w_{i,j}$와 $w_{i,l}$이 각각 $<\mathbf{v}_i, \mathbf{v}_j>$와 $<\mathbf{v}_i, \mathbf{v}_l>$로 나누어지니 둘은 공유하는 parameter가 존재하는 셈

B. Parameter Estimation Under Sparsity

그럼 왜 SVM은 sparse한 데이터에서 실패할까?

• CF를 할 때 데이터가 sparse한 상황을 가정하면, $Figure 1$에서 볼 수 있듯이 유저나 아이템(영화)의 binary 표현에서 1로 차 있는 경우는 매우 적고 대부분이 0으로 차 있음

다시 kernel에 따라 나누어서 왜 실패하는지 살펴보자

1) Linear SVM

• linear kernel일 때 linear SVM은 아래와 같이 변형할 수 있음
  
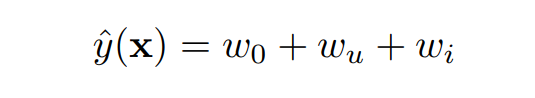
• 이는 $x_j = 1$이라면 $j = u$이거나 $j = i$ (관계가 아닌 개별적인 값을 의미)
• 즉 이 모델은 CF에서 유저나 아이템 값이 파악되었을 때의 CF와 동일(where only the user and item biases are captured)
• 모델이 간단하기 때문에 sparse한 데이터라도 parameter의 추정은 쉽지만, 예측 성능은 낮음($Figure 2$ 참고)

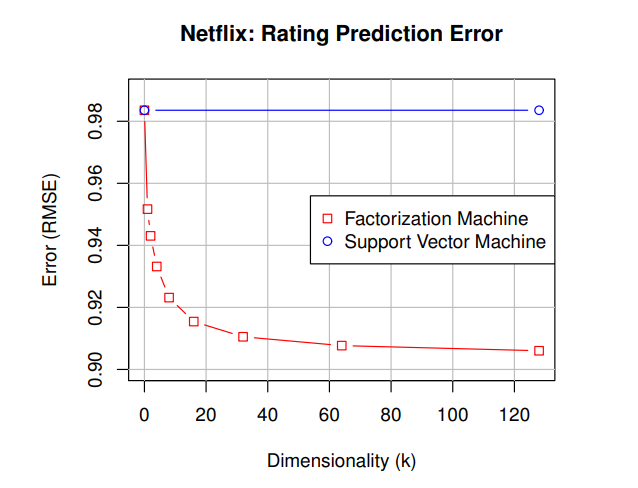
2) Polynomial SVM

• polynomial kernel일 때 고차원의 상호작용을 표현하게 됨
• $m(\mathbf{x}) = 2$라면, Polynomial SVM은 아래와 같이 표현할 수 있음
  
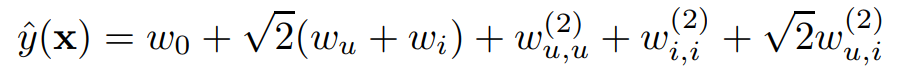
• $w_u$와 $w_{u,u}^{(2)}$는 같은 표현이라 하나는 뗄 수 있음
• 그럼 linear일 때에서 $w_{u,i}^{2}$가 추가된 것과 같음
• CF에서 $w_{u,i}^{2}$는 training data에서 관측된 하나의 $(u,i)$에 대한 것
• test data에 $(u',i')$이 있다면 해당 상호작용에 대한 parameter는 모두 0으로 예측함
  • 이에 대해서는 관측한 바가 없기 때문임. 모든 상호작용은 독립적이라서.
  • 파악된 상호작용 값에 대해서만 의존(the polynomial SVM only relies on the user and item biases)
  • $(i,j)$ 쌍의 상호작용에 대해서는 0이 아닌 충분한 $\mathbf{x} \in D$가 존재해야 $w_{i,j}^{(2)}$ parameter를 예측할 때 사용할 수 있음
• 이는 Polynomial SVM이 2-way 상호작용을 예측하는 데에 사용할 수 없다는 것과 linear SVM보다 좋은 추정을 할 수 없음을 의미
• CF의 상황에서뿐 아니라 데이터가 매우 sparse한 다른 경우에도 고차원의 상호작용을 추정하는 것이 문제가 됨
• 그러므로 sparse 데이터의 상황에서는 SVM은 실패할 가능성이 높음

C. Summary

• SVM의 조밀한 매개변수화는 상호작용의 직접적인 관찰(training set에 있어야 함)이 필요하지만, FM은 그렇지 않으므로 sparsity에서도 parameter를 잘 추정할 수 있음
• FM은 primal에서 직접 학습이 가능하지만 non-linear SVM은 dual에서 학습
• FM의 model equation은 training data와 무관하지만 SVM은 training data의 일부에 의존적임(support vector)

5. FMs VS. OTHER FACTORIZATION MODELS

SVM과의 차이는 알겠는데, 다른 factorization model과는 어떻게 다를까?

• 다양한 factorization model이 존재
  • categorical 변수의 m-ary 관계에 대한 일반적인 모델(MF, PARAFAC)
  • 특정한 데이터와 작업에 맞춰진 모델(SVD++, PITF, FPMC)
• FM에 정확한 input data(feature vector $\mathbf{x}$)를 넣음으로써 어떻게 이들을 모방할 수 있는지 알아보자

특정한 기능을 하는 해당 모델들을 input 한정을 통해 모방하겠다!

A. Matrix and Tensor Factorization

• MF는 가장 많이 연구된 factorization model 중 하나
• 이는 $U, I$ 관계를 factorizing (latent factor)하여 각각을 binary indicator로 정의하는 방식 사용
  • $Figure 1$에서 유저와 아이템(영화)를 binary로 표현한 것과 동일
    
• 위와 같은 feature vector $\mathbf{x}$를 사용하는 FM은 MF의 효과를 낼 수 있음
• 왜냐하면 위의 $x_j$는 $u$와 $i$에 대해 0이 아닌 값(즉 $u$와 $i$의 상호작용이 있는 값)인데, FM을 아래와 같이 표현
  
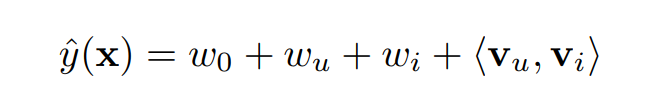
• global bias와 유저, 아이템 bias에 $\mathbf{v}_u, \mathbf{v}_i$의 상호작용이 반영

B. SVD++

• 순위 예측(회귀) 작업에서 Korem이 MF를 SVD++로 발전시킴
  
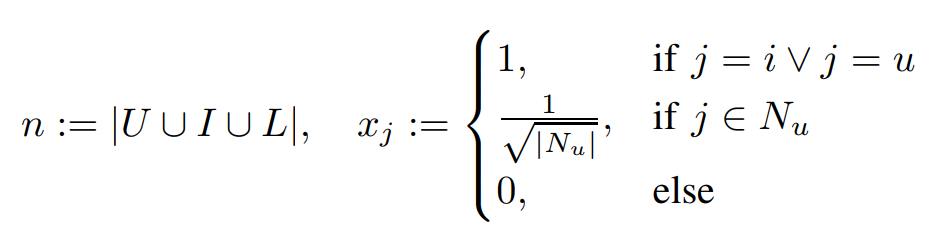
• 위와 같은 feature vector $\mathbf{x}$를 사용하는 FM은 SVD++의 효과를 낼 수 있음
• $N_u$는 유저가 이전에 평가한 전체 영화의 집합
• d = 2일 때 FM은 아래와 같이 표현
  
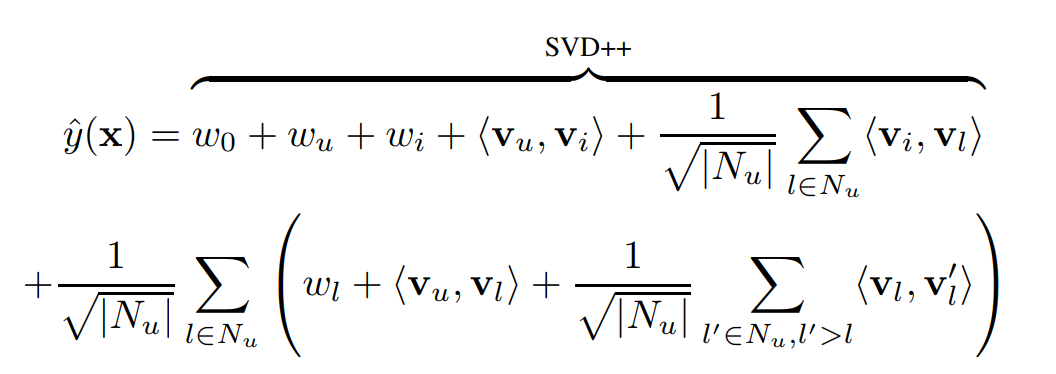
• 첫 부분은 SVD++와 동일하지만 추가적인 유저-$N_u$ 상호작용이나 $N_u$-$N_u$ 상호작용을 표현하는 추가적인 부분이 존재

C. PITF for Tag Recommendation

• tag 예측 문제는 유저와 아이템 결합에 대한 순위 태그를 정의하는 것과 같음
• PITF가 Tag Recommendation에 대한 ECML/PKDD Discovery Challenge에서 가장 우수한 성적
• FM에서 binary indicator 변수로 유저 $u$, 아이템 $i$, 태그 $t$를 나타내는 것은 아래와 같음
  
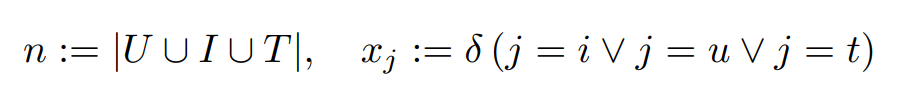
• 그리고 이것은 FM을 아래와 같이 쓸 수 있게 함
  
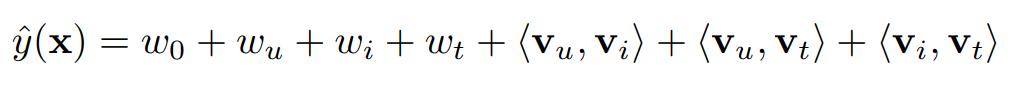
• 같은 유저, 아이템 조합 $(u, i)$에 대한 두 가지 태그 $t_A, t_B$ 사이의 순위에 사용되기 때문에 $(u,i,t_A)$와 $(u,i,t_B)$ 사이의 차이에 대해 최적화와 예측이 작동. 그래서 또 아래와 같이 쓸 수 있음
  
• 이제 PITF 모델과 binary indicator를 사용한 FM 모델은 거의 동일
• 물론 조금 차이가 있긴 함
  • FM은 $t$에 대한 bias 값 $w_t$ 존재
  • 태그에 대한 parameter $\mathbf{v}_t$는 FM에서 $(u, t)$와 $(i, t)$ 상호작용에서 공유하지만 PITF에서는 개별적임
• 이로써 PITF와 FM이 성능 면에서도 유사하다는 것은 $Figure 3$에 나와 있음
  
  $Figure 3$

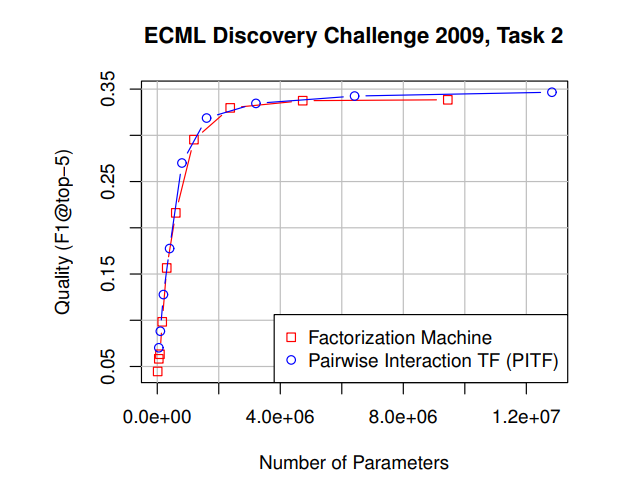
D. Factorized Personalized Markov Chains (FPMC)

• 온라인 쇼핑몰에서의 유저의 마지막 구매 기반 상품 순위 정렬 모델
• 아래와 같은 feature vector를 사용
  
• $B_t^u$는 유저 $u$가 시간 $t$ 때 구매한 모든 아이템 바구니
• 그럼 d = 2일 때 FM은 아래와 같이 쓸 수 있음
  
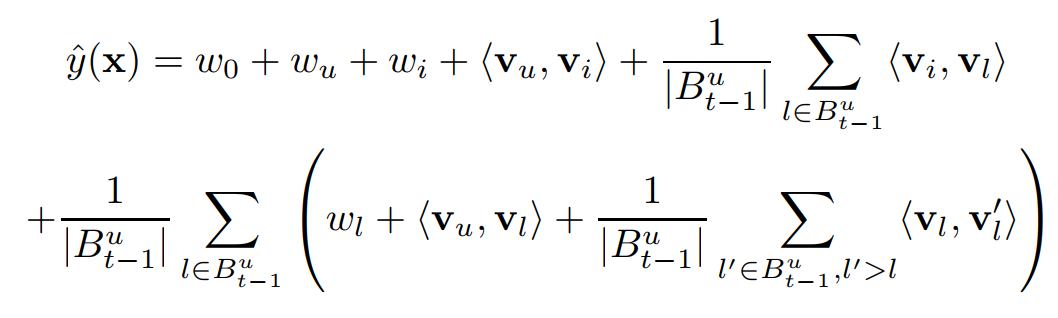
• tag recommendation에서처럼 이 모델은 순위 작업에 사용됨 그래서 $(u,i_A,t)$와 $(u,i_B,t)$ 사이의 점수 차이가 예측 및 최적화의 기준
• 그러므로 추가적인 항 중에 $i$에 대한 것이 아니면 사라지고, FM 식은 아래처럼 변환
  
• FPMC와 FM은 거의 같아지게 됨
• 물론 이것도 차이는 조금 있음
  • FM에는 추가적인 아이템 bias인 $w_i$가 존재
  • FM은 $(u, i)$와 $(i,l)$ 사이의 상호작용에서 factorization parameter를 공유

E. Summary

• PARAFAC이나 MF와 같은 표준 factorization model은 FM과 같은 일반적인 예측 모델이 아님. 대신 이들은 feature vector가 $m$개의 부분으로 나뉘고, 각각의 부분에서 정확히 하나의 요소만 1이고 나머지는 0이어야 함($Figure 1$에서의 유저 및 아이템 표현 방식)
• 단일 작업을 위해 설계된 specialized factorization models(위에서 살펴 본 모델들)가 존재. FM이 적용하기 쉽게 만드는 feature extraction(featuer vector)을 통해 다양한 factorization models을 모방할 수 있음

6. CONCLUSION AND FUTURE WORK

• FM(factorization machines)을 소개
• FM은 SVM의 generality와 factorization models의 이점을 통합
• SVM과 비교하면
  • FM은 매우 sparse한 상태에서도 parameter 추정이 가능
  • FM의 model equation은 선형이므로 model parameter에만 의존(support vector가 필요 없다는 뜻)
  • FM은 primal에서 직접 최적화 가능
• FM의 표현력은 Polynomial SVM와 비슷, 모든 실수 값 벡터를 처리할 수 있는 general predictor
• 적절한 input feature vector를 사용함으로써, 하나의 특정한 작업을 하는 수많은 모델들(MF, SVD++, PITF, FPMC)과 동일하거나 매우 유사한 기능을 할 수 있음